图论2（DFS和BFS相关问题）

一，寻路问题

1，迷宫

问题描述

有一迷宫，从起点1,1到终点4,3，输出所有走的路径和最短路径长度

  • 边界0

  • 空地1

  • 障碍物2

样例输入

  5  4
  1 1 2 1
  1 1 1 1
  1 1 2 1
  1 2 1 1
  1 1 1 2
  1 1 4 3

5代表5行，4代表4列，下面每个数字代表迷宫每个格子是边界还是空地还是障碍物

思路分析（BFS,DFS）

代码实现

BFS(只输出了最短路径和最短路径长度)
package BFS;

//------------------------------------------------------------------
//        迷宫问题
//------------------------------------------------------------------
//        起点1,1
//        终点4,3
//------------------------------------------------------------------
//        5行4列
//------------------------------------------------------------------
//        边界0，空地1，障碍物2
//------------------------------------------------------------------
//        输入
//        5  4
//        1 1 2 1
//        1 1 1 1
//        1 1 2 1
//        1 2 1 1
//        1 1 1 2
//        1 1 4 3

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class Main {
    public static Queue<GZ> queue = new LinkedList<GZ>();
    public static int xp[] = {0, 1, 0, -1};
    public static int yp[] = {1, 0, -1, 0};

    public static void main(String[] args) {
        Scanner s = new Scanner(System.in);
        int m = s.nextInt();
        int n = s.nextInt();
        int arr[][] = new int[m + 1][n + 1];
        int vic[][] = new int[m + 1][n + 1];
        int p = 4, q = 3;

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                arr[i][j] = s.nextInt();
            }
        }
        StringBuilder lj = new StringBuilder();
        lj.append("(1,1)->");
        GZ gz = new GZ(1, 1, 0, lj);
        vic[1][1] = 1;
        queue.offer(gz);
        while (queue.peek() != null) {
            GZ g = queue.poll();
            if (g.x == p && g.y == q) {
                System.out.println();
                System.out.println(g.step);
                String substring = g.lj.toString().substring(0, g.lj.length() - 2);
                System.out.println(substring);
                break;
            }

            for (int i = 0; i < 4; i++) {
                int a = g.x + xp[i];
                int b = g.y + yp[i];
                //排除越界
                if (a <= 0 || b <= 0 || a > m || b > n) {
                    continue;
                }
                //空白格子且未访问
                if (arr[a][b] == 1 && vic[a][b] == 0) {
                    vic[a][b] = 1;
                    String ljd = g.lj.toString();
                    StringBuilder ljds = new StringBuilder(ljd);
                    ljds.append("(").append(a).append(",").append(b).append(")->");
                    queue.add(new GZ(a, b, g.step + 1, ljds));
                }
            }
        }
    }

}


class GZ {
    int x;
    int y;
    int step;
    StringBuilder lj;

    public GZ(int x, int y, int step, StringBuilder lj) {
        this.x = x;
        this.y = y;
        this.step = step;
        this.lj = lj;
    }

    public GZ() {


    }
}
DFS
package DFS;

import java.util.Scanner;

//------------------------------------------------------------------
//        迷宫问题
//------------------------------------------------------------------
//        起点1,1
//        终点4,3
//------------------------------------------------------------------
//        5行4列
//------------------------------------------------------------------
//        边界0，空地1，障碍物2
//------------------------------------------------------------------
//        输入
//        5  4
//        1 1 2 1
//        1 1 1 1
//        1 1 2 1
//        1 2 1 1
//        1 1 1 2
//        1 1 4 3
public class Main {
    //终点行坐标
    public static int p;
    //终点列坐标
    public static int q;
    //顺时针寻找，横纵偏移
    public static int xp[] = {0, 1, 0, -1};
    public static int yp[] = {1, 0, -1, 0};
    //最小步数
    public static int min = -1;
    //
    public static int arr[][];
    public static int vic[][];
    public static int m;
    public static int n;
    public static void main(String[] args) {
        Scanner s = new Scanner(System.in);
        //1.设置迷宫大小
         m = s.nextInt();
         n = s.nextInt();
        //2.填充迷宫
        arr = new int[m+1][n+1];
        vic = new int[m+1][n+1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                arr[i][j] = s.nextInt();
            }
        }

        //3.起点1,1,终点4,3
        p = 4;
        q = 3;
       //4.dfs
        int x = 1;
        int y = 1;
        StringBuilder lj=new StringBuilder();
        lj.append("(").append(x).append(",").append(y).append(")->");
        dfs(x, y, 0,lj);
        System.out.println(min);
    }

    private static void dfs(int x, int y, int step,StringBuilder lj) {
        if (x == p && y == q) {
            String substring = lj.substring(0, lj.length() - 2);
            System.out.println(substring.toString());
            if (min == -1 || min > step) {
                min = step;
            }
            return;
        }

        for (int i = 0; i < 4; i++) {
            int a,b;
            a = x + xp[i];
            b = y + yp[i];
            //越界跳过
            if(a>m||b>n||a<=0||b<=0){
                continue;
            }
            if (arr[a][b] == 1 && vic[a][b] == 0) {
                lj.append("(").append(a).append(",").append(b).append(")->");
                vic[a][b] = 1;
                dfs(a, b, step + 1,lj);
                vic[a][b] = 0;
            }

        }

    }

}

2，岛屿最大面积

问题描述

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

 

示例 1：

输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

提示：

  • m == grid.length

  • n == grid[i].length

  • 1 <= m, n <= 50

  • grid[i][j] 为 0 或 1

思路分析（DFS寻路）

代码实现

DFS
class Solution {
    public int count = 0;
    public int[] xp = { 0, 1, 0, -1 };
    public int[] yp = { 1,0 , -1, 0 };

    public int maxAreaOfIsland(int[][] grid) {
        int max = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == 1) {
                    dfs(i, j, grid);
                    max = Math.max(max, count);
                    count = 0;
                }
            }
        }
        return max;

    }

    private void dfs(int x, int y, int[][] grid) {
        grid[x][y] = 0;
        count++;
        // TODO Auto-generated method stub
        for (int i = 0; i < 4; i++) {
            int xd = x + xp[i];
            int yd = y + yp[i];
            if (xd < 0 || yd < 0 || xd >= grid.length || yd >= grid[0].length) {
                continue;
            }
            if (grid[xd][yd] == 1) {
                dfs(xd, yd, grid);
            }
        }

    }
}

参考链接：https://leetcode-cn.com/problems/max-area-of-island/submissions/

3.，岛屿数量

问题描述

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [ ["1","1","1","1","0"], ["1","1","0","1","0"], ["1","1","0","0","0"], ["0","0","0","0","0"] ] 输出：1 示例 2：

输入：grid = [ ["1","1","0","0","0"], ["1","1","0","0","0"], ["0","0","1","0","0"], ["0","0","0","1","1"] ] 输出：3

提示：

  • m == grid.length

  • n == grid[i].length

  • 1 <= m, n <= 300

  • gridi 的值为 '0' 或 '1'

 

思路分析

代码实现

BFS
class Solution {
//    //0没有访问，1访问过
//    public static int vic[][];
    public static int xp[]= {0,1,0,-1};
    public static int yp[]= {1,0,-1,0};
    public int numIslands(char[][] grid) {
        int number=0; 
        for(int i=0;i<grid.length;i++) {
            for(int j=0;j<grid[0].length;j++) {
                if(grid[i][j]=='1') {
                    number++;
                    bfs(i,j,grid);
                }
            }
        }
        return number;
    }

    private void bfs(int x, int y, char[][] grid) {
        // TODO Auto-generated method stub
        Queue<GZ>queue=new LinkedList<>();
        queue.offer(new GZ(x,y));
        GZ gz=null;
        while((gz=queue.poll())!=null) {
            for(int i=0;i<4;i++) {
                int xd=gz.x+xp[i];
                int yd=gz.y+yp[i];
                if(xd<0||xd>=grid.length||yd<0||yd>=grid[0].length) {
                    continue;
                }
                if(grid[xd][yd]!='0') {
                    grid[xd][yd]='0';
                    queue.offer(new GZ(xd,yd));
                }
            }
            
        }
        
    }
}
class GZ{
    public int x;
    public int y;
    public GZ(int x,int y) {
        this.x=x;
        this.y=y;
    }
    public GZ() {
        
    }
}
DFS
class Solution {
    public static int xp[]= {0,1,0,-1};
    public static int yp[]= {1,0,-1,0};
    public int numIslands(char[][] grid) {
        int number=0; 
        for(int i=0;i<grid.length;i++) {
            for(int j=0;j<grid[0].length;j++) {
                if(grid[i][j]=='1') {
                    number++;
                    dfs(i,j,grid);
                }
            }
        }
        return number;
    }
    private void dfs(int x, int y,char[][]grid) {
        
        for(int i=0;i<4;i++) {
            int xd=x+xp[i];
            int yd=y+yp[i];
            if(xd<0||xd>=grid.length||yd<0||yd>=grid[0].length) {
                continue;
            }
            if(grid[xd][yd]!='0') {
                grid[xd][yd]='0';
                dfs(xd, yd, grid);
            }
        }
        
    }
}

参考链接：https://leetcode-cn.com/problems/number-of-islands

4，岛屿周长

问题描述

给定一个 row x col 的二维网格地图 grid ，其中：gridi = 1 表示陆地， gridi = 0 表示水域。

网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

示例 1：

输入：grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]] 输出：16 解释：它的周长是上面图片中的 16 个黄色的边 示例 2：

输入：grid = [[1]] 输出：4 示例 3：

输入：grid = [[1,0]] 输出：4

提示：

  • row == grid.length

  • col == grid[i].length

  • 1 <= row, col <= 100

  • gridi 为 0 或 1

思路分析

代码实现

DFS

class Solution {
    public int[][] grid;
    public int[][] vic;
    public int xp[]= {0,1,0,-1};
    public int yp[]= {1,0,-1,0};
    public int len=0;
    public int islandPerimeter(int[][] grid) {
        this.grid=grid;
        vic=new int[grid.length][grid[0].length];
        for(int i=0;i<grid.length;i++) {
            for(int j=0;j<grid[0].length;j++) {
                if(grid[i][j]==1&&vic[i][j]==0) {
                    vic[i][j]=1;
                    dfs(i,j);
                    //只有一个岛屿，找到就break
                    break;
                }
            }
        }
        return len;
    }

    private int dfs(int x, int y) {
        // TODO Auto-generated method stub
        
        
        
        for(int i=0;i<4;i++) {
            int xd=x+xp[i];
            int yd=y+yp[i];
            if(xd<0||yd<0||xd>=grid.length||yd>=grid[0].length||grid[xd][yd]==0) {
                len+=1;
                continue;
            }
            if(vic[xd][yd]==1) {
                continue;
            }
            vic[xd][yd]=1;
            dfs(xd, yd);
        }
        return len;
    }
}

参考链接：https://leetcode-cn.com/problems/island-perimeter

5，方格分割

问题描述

6x6的方格，沿着格子的边线剪开成两部分。 要求这两部分的形状完全相同。

如下就是三种可行的分割法。

 

 

 

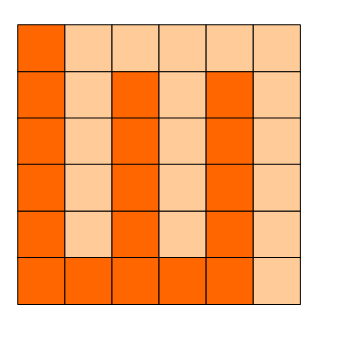
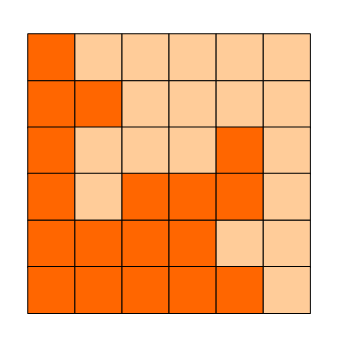
思路分析

代码实现

package fgfg;


public class Main {
    public static int[] xp = { 0, 1, 0, -1 };
    public static int[] yp = { 1, 0, -1, 0 };
    public static int[][] vic = new int[7][7];
    public static int count = 0;

    public static void main(String[] args) {
        vic[3][3] = 1;
        dfs(3, 3);
        System.out.println(count/4);
    }

    public static void dfs(int x, int y) {
        
        for (int i = 0; i < 4; i++) {
            int xd = x + xp[i];
            int yd = y + yp[i];
            if (xd <= 0 || yd <= 0 || xd >= 6 || yd >= 6) {
                count++;
                continue;
            }
            if (vic[xd][yd] == 0) {
                vic[xd][yd] =vic[6-xd][6-yd]= 1;
                dfs(xd, yd);
                vic[xd][yd]= vic[6-xd][6-yd]= 0;
            }
        }
    }
}

参考链接：https://www.lanqiao.cn/problems/1629/learning/?is_contest=true

 二，找数问题

1，找满足条件的四个数（排列组合）

问题描述

给定一个1～N的排列a[i]，每次将相邻两个数相加，得到新序列，再对新序列重复这样的操作，显然每次得到的序列都比上一次的序列长度少1，最终只剩一个数字。 　　例如: 　　3 1 2 4 　　4 3 6 　　7 9 　　16 　　现在如果知道N和最后得到的数字sum，请求出最初序列a[i]，为1～N的一个排列。若有多种答案，则输出字典序最小的那一个。数据保证有解。 输入 4 16 输出 3 1 2 4

思路分析（BFS，DFS）

代码实现

BFS
package BFS;

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

//　给定一个1～N的排列a[i]，每次将相邻两个数相加，得到新序列，再对新序列重复这样的操作，显然每次得到的序列都比上一次的序列长度少1，最终只剩一个数字。
//        　　例如:
//        　　3 1 2 4
//        　　4 3 6
//        　　7 9
//        　　16
//        　　现在如果知道N和最后得到的数字sum，请求出最初序列a[i]，为1～N的一个排列。若有多种答案，则输出字典序最小的那一个。数据保证有解。
//输入
//4 16
//输出
//3 1 2 4
public class Main2 {
    public static Queue<SZ> queue = new LinkedList<>();

    public static void main(String[] args) {
        Scanner s = new Scanner(System.in);
        int n = s.nextInt();
        int sum = s.nextInt();

        for (int i = 0; i < n; i++) {
            int arr[] = new int[n];
            int step = 0;
            arr[step] = i + 1;
            SZ sz = new SZ(arr, step);
            sz.vic[i] = 0;
            queue.offer(sz);
        }

        while (queue.peek() != null) {
            SZ sz = queue.poll();
            if (sz.step == 3) {
                int[] arr=sz.arr;
                int[] arr1=Arrays.copyOf(arr,arr.length);
                for(int i=1;i<n;i++){
                    for(int j=0;j<n-i;j++){
                        arr1[j]=arr1[j]+arr1[j+1];
                    }
                }
                if(arr1[0]==sum){
                    StringBuilder str=new StringBuilder();
                    for(int i=0;i<n;i++){
                        str.append(arr[i]).append(" ");
                    }
                    System.out.println(str.toString());
                    break;
                }
               continue;
            }

            for (int i = 0; i < n; i++) {
                if (sz.vic[i] != 0) {
                    int[] arr =  Arrays.copyOf(sz.arr,sz.arr.length);
                    int step=sz.step+1;
                    arr[step] = sz.vic[i];
                    SZ szt = new SZ(arr, step);
                    szt.vic=Arrays.copyOf(sz.vic,sz.vic.length);
                    szt.vic[i] = 0;
                    queue.offer(szt);
                }
            }
        }

    }

    static class SZ {
        int arr[];
        int vic[] = {1, 2, 3, 4};
        int step;

        public SZ() {

        }

        public SZ(int arr[], int step) {
            this.step = step;
            this.arr = arr;
        }
    }
}
DFS
package DFS;

import java.util.Arrays;
import java.util.Scanner;

//　给定一个1～N的排列a[i]，每次将相邻两个数相加，得到新序列，再对新序列重复这样的操作，显然每次得到的序列都比上一次的序列长度少1，最终只剩一个数字。
//        　　例如:
//        　　3 1 2 4
//        　　4 3 6
//        　　7 9
//        　　16
//        　　现在如果知道N和最后得到的数字sum，请求出最初序列a[i]，为1～N的一个排列。若有多种答案，则输出字典序最小的那一个。数据保证有解。
//输入
//4 16
//输出
//3 1 2 4
public class Main2 {
    public static Boolean flag=true;
    public static int n;
    public static int sum;
    public static  int vic[];
    public static void main(String[] args) {
        Scanner s=new Scanner(System.in);
         n = s.nextInt();
        sum=s.nextInt();
        vic=new int[n+1];
        int arr[]=new int[n];
        dfs(arr,0);
    }

    private static void dfs(int[] arr,  int step) {
        if (step == n) {
            int[] arr1= Arrays.copyOf(arr,arr.length);
            for(int i=1;i<n;i++){
                for(int j=0;j<n-i;j++){
                    arr1[j]=arr1[j]+arr1[j+1];
                }
            }
            if(arr1[0]==sum){
                flag=false;
                StringBuilder str=new StringBuilder();
                for(int a:arr){
                    str.append(a).append(" ");
                }
                System.out.println(str.toString());
            }
            return;
        }
        if (flag) {
            for (int i = 1; i <= n; i++) {
                int t = i;
                if (vic[i] == 0) {
                    arr[step] = i;
                    vic[i] = 1;
                    dfs(arr, step + 1);
                    vic[i] = 0;
                }
            }
        }
    }
}

2.输出子集

问题描述

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3] 输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]] 示例 2：

输入：nums = [0] 输出：[[],[0]]

提示：

  • 1 <= nums.length <= 10

  • -10 <= nums[i] <= 10

  • nums 中的所有元素 互不相同

思路分析

代码实现

DFS
class Solution {
    public int[] nums;
    public List<List<Integer>> list;
    public List<List<Integer>> subsets(int[] nums) {
        this.nums = nums;
         list = new ArrayList<List<Integer>>();
        list.add(new ArrayList<>());
        for (int i = 0; i < nums.length; i++) {
            
            for (int j = 1; j <=nums.length; j++) {
                Integer[]num=new Integer[j];
                dfs(i, j, 1, num);
            }
        }
        return list;
    }

    private void dfs(int begin, int number, int step, Integer[]num) {
        // TODO Auto-generated method stub
        num[step-1]=nums[begin];
        if (step == number) {
            List<Integer>list2=new ArrayList<>();
            for(int i=0;i<num.length;i++) {
                list2.add(num[i]);
            }
            list.add(list2);
            return;
        }
        for (int i = begin + 1; i < nums.length; i++) {
            dfs(i, number, step + 1, num);
        }
    }
}

参考链接：https://leetcode-cn.com/problems/subsets

3，等差素数列

问题描述

2,3,5,7,11,13,.... 是素数序列。 类似：7,37,67,97,127,1577,37,67,97,127,157 这样完全由素数组成的等差数列，叫等差素数数列。

上边的数列公差为 3030，长度为 66。

20042004 年，格林与华人陶哲轩合作证明了：存在任意长度的素数等差数列。 这是数论领域一项惊人的成果！

有这一理论为基础，请你借助手中的计算机，满怀信心地搜索：

长度为 1010 的等差素数列，其公差最小值是多少？

思路分析

代码实现

package susc;

import java.util.ArrayList;
import java.util.List;

//长度为 1010 的等差素数列，其公差最小值是多少？
public class Main {
    public static List<Integer> list = new ArrayList<>();

    public static void main(String[] args) {
        // 添加到10000的素数
        for (int i = 2; i < 10000; i++) {
            if (isSuShu(i)) {
                list.add(i);
            }
        }
        for (int i = 0; i < list.size(); i++) {
            for (int j = 1; j < 1000; j++) {
                dfs(i, j, list.get(i), 1);
            }
        }

    }

    private static Boolean dfs(int begin, int dc, Integer lastShu, int step) {
        // TODO Auto-generated method stub
        if (step == 10) {
            System.out.println(dc);
            return true;
        }

        for (int i = begin + 1; i < list.size(); i++) {
            Integer shu = list.get(i);
            if ((shu - lastShu) == dc) {
                dfs(i, dc, shu, step + 1);
            }

            if ((shu - lastShu) > dc) {
                return false;
            }

        }

        return false;
    }

    public static Boolean isSuShu(int shu) {
        Boolean flag = true;
        if (shu < 2) {
            flag = false;
        }
        for (int i = 2; i <= Math.sqrt(shu); i++) {
            if (shu % i == 0) {
                flag = false;
            }
        }
        return flag;
    }

}

参考链接：https://www.lanqiao.cn/problems/646/learning/?is_contest=true

三，dfs搜图问题

1，L3-025 那就别担心了

问题描述

下图转自“英式没品笑话百科”的新浪微博 —— 所以无论有没有遇到难题，其实都不用担心。

 

博主将这种逻辑推演称为“逻辑自洽”，即从某个命题出发的所有推理路径都会将结论引导到同一个最终命题（开玩笑的，千万别以为这是真正的逻辑自洽的定义……）。现给定一个更为复杂的逻辑推理图，本题就请你检查从一个给定命题到另一个命题的推理是否是“逻辑自洽”的，以及存在多少种不同的推理路径。例如上图，从“你遇到难题了吗？”到“那就别担心了”就是一种“逻辑自洽”的推理，一共有 3 条不同的推理路径。

输入格式

输入首先在一行中给出两个正整数 N（1<N≤500）和 M，分别为命题个数和推理个数。这里我们假设命题从 1 到 N 编号。

接下来 M 行，每行给出一对命题之间的推理关系，即两个命题的编号 S1 S2，表示可以从 S1 推出 S2。题目保证任意两命题之间只存在最多一种推理关系，且任一命题不能循环自证（即从该命题出发推出该命题自己）。

最后一行给出待检验的两个命题的编号 A B。

输出格式

在一行中首先输出从 A 到 B 有多少种不同的推理路径，然后输出 Yes 如果推理是“逻辑自洽”的，或 No 如果不是。

题目保证输出数据不超过 109。

输入样例1

7 8
7 6
7 4
6 5
4 1
5 2
5 3
2 1
3 1
7 1

输出样例1

3 Yes

输入样例2

7 8
7 6
7 4
6 5
4 1
5 2
5 3
6 1
3 1
7 1

输出样例2

3 No

思路分析

这题的大意是从A到B有多少条路径，从A出发，可能有多条路径，但最后的终点必须是B，要不然就不是逻辑自洽了，由于是有向无环图，不用考虑从A到B再到A的循环情况，所以可以不用vic

代码实现

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.Scanner;

public class Main {
    public Boolean flag = true;
    public int[] dot = null;
    public static Map<Integer, List<Integer>> map = new HashMap<>();

    public static void main(String[] args) {
        Scanner sca = new Scanner(System.in);
        int n = sca.nextInt();
        int m = sca.nextInt();
        Main main = new Main();
        main.dot = new int[n + 1];
        for (int i = 0; i < main.dot.length; i++) {
            main.dot[i] = -1;
        }
        // 有向无环图，邻接表
        for (int i = 0; i < m; i++) {
            Integer start = sca.nextInt();
            Integer end = sca.nextInt();
            List<Integer> list = map.getOrDefault(start, new ArrayList<>());
            list.add(end);
            map.put(start, list);
        }
        int startQ = sca.nextInt();
        int endQ = sca.nextInt();
        int result = main.dfs(startQ, endQ);
        String str = main.flag == true ? "Yes" : "No";
        System.out.println(result + " " + str);
    }

    private int dfs(int startQ, int endQ) {
        // TODO Auto-generated method stub
        int result = 0;
        if (dot[startQ] != -1) {
            return dot[startQ];
        }
        if (startQ == endQ) {
            return 1;

        }
        List<Integer> list = map.get(startQ);
        if (list == null) {
            flag = false;
            return dot[startQ] = 0;
        }
        for (Integer d : list) {
            result += dfs(d, endQ);
        }
        return dot[startQ] = result;
    }
}

题目链接：https://pintia.cn/problem-sets/994805046380707840/problems/1336215880692482060

2，危险系数（蓝桥杯）

题目描述

问题描述 抗日战争时期，冀中平原的地道战曾发挥重要作用。 地道的多个站点间有通道连接，形成了庞大的网络。但也有隐患，当敌人发现了某个站点后，其它站点间可能因此会失去联系。 我们来定义一个危险系数DF(x,y)： 对于两个站点x和y (x != y), 如果能找到一个站点z，当z被敌人破坏后，x和y不连通，那么我们称z为关于x,y的关键点。相应的，对于任意一对站点x和y，危险系数DF(x,y)就表示为这两点之间的关键点个数。 本题的任务是：已知网络结构，求两站点之间的危险系数。

输入

输入数据第一行包含2个整数n(2 < = n < = 1000), m(0 < = m < = 2000),分别代表站点数，通道数； 接下来m行，每行两个整数 u,v (1 < = u, v < = n; u != v)代表一条通道； 最后1行，两个数u,v，代表询问两点之间的危险系数DF(u, v)。

输出

一个整数，如果询问的两点不连通则输出-1.

样例输入

7 6
1 3
2 3
3 4
3 5
4 5
5 6
1 6

样例输出

2

思路分析

询问通道是否连通，也就是能走到就true，不能走到就false

关键点，也就是起点到终点无论怎么走也必须经过的点，转换一下，

假如起点到终点有t条路径，也就是说必定经过关键点t次（除起点和终点）

也就是说从起点到终点，经过t次的点就是我们要找的点（除起点和终点）

代码实现

package DayT2;

import java.util.Scanner;

public class Main {
    // 记录顶点个数
    public int n;
    // 记录通道连通情况
    public int[][] arr = null;
    // 记录终点
    public int endQ = -1;
    // 记录能否到终点
    public Boolean flag = false;
    // 记录从起点到终点不同路径下每个点经过的次数（不算起点）
    public int[] dot = null;
    // dfs的vic
    public int[] vic = null;

    public static void main(String[] args) {
        Scanner sca = new Scanner(System.in);
        Main main = new Main();
        //接收顶点数和边数
        main.n = sca.nextInt();
        int m = sca.nextInt();
        main.init();
        //由于是无向图，所以构建邻接矩阵
        for (int i = 0; i < m; i++) {
            int start = sca.nextInt();
            int end = sca.nextInt();
            // 站点x和y连通，也就是说能从x到y，也能从y到x
            main.arr[start][end] = main.arr[end][start] = 1;
        }
        //接收起点，终点
        int startQ = sca.nextInt();
        main.endQ = sca.nextInt();
        //dfs
        int result = main.dfs(startQ, 0, new int[main.n + 1]);
        int count = 0;
        //如果两个点不连通，输出-1
        if(main.flag==false) {
            System.out.println(-1);
        }
        //记录有多少个点是去终点的必经之点
        for (int i = 1; i < main.n + 1; i++) {
            if (main.dot[i] == result) {
                count++;
            }
        }
        // 减去终点
        System.out.println(count - 1);

    }
    private void init() {
        // TODO Auto-generated method stub
        arr = new int[n + 1][n + 1];
        dot = new int[n + 1];
        vic = new int[n + 1];
    }
    /**
     * 
     * @param startQ:到达的点
     * @param step:第几个经过点，0代表起点
     * @param temp:从起点到终点经过的点的数组
     * @return
     */
    private int dfs(int startQ, int step, int[] temp) {
        // TODO Auto-generated method stub
        //如果到达的点为终点，说明已经到了终点，有一条路径了
        if (startQ == endQ) {
            //将从起点到终点经过点的次数加一
            for (int i = 0; i < step; i++) {
                dot[temp[i]]++;
            }
            flag = true;
            return 1;
        }
        int result = 0;
        //遍历该点能到的点
        for (int i = 1; i < n + 1; i++) {
            //如果访问过，continue
            if (vic[i] == 1) {
                continue;
            }
            //如果不连通，continue
            if (arr[startQ][i] == 0) {
                continue;
            }
            //记录经过的点
            temp[step] = i;
            //dfs
            vic[i] = 1;
            result += dfs(i, step + 1, temp);
            vic[i] = 0;
        }
        //返回从startQ到终点路径条数
        return result;

    }
}

题目链接：https://www.dotcpp.com/oj/problem1433.html

 

posted @ 2022-04-13 16:51  lzstar-A2  阅读(35)  评论(0)  编辑  收藏  举报