从马尔可夫模型（Markov model）到卡尔曼滤波（Kalman filtering）

目录

• 马尔可夫模型（Markov model）
• 隐马尔可夫模型（Hidden Markov model）
• 卡尔曼滤波（Kalman filtering）
• 简单总结

      卡尔曼滤波(Kalman Filtering)是一个知名度颇高的数据处理方法（至少名字挺咋呼），本文尝试提供一个对它的简单理解 :)

马尔可夫模型（Markov model）

 

 

 

 

        马尔可夫模型是一个研究离散时间随机过程（Xi, i = 1, 2, ,3 ,4 ...）的方法。它的主要思想是将各个事件Xi的互相影响区分开：假设每一个事件xi只与前一次发生的事件Xi-1直接相关，而与再之前的事件Xi-2, Xi-3等不直接产生关系。用条件概率的形式表达就是：

P(Xi | X0, X1, X2...Xi-2, Xi-1) = P(Xi | Xi-1) （对于判断Xi的状况，一旦知道Xi-1，其余Xi-2,...X0等事件就不能再提供额外的信息）

        这种简化看似太过理想（每个事件仅直接影响下一个事件，而不直接影响之后的事件），但在实践中却表现颇佳，在我看来原因有二：一是在日常现象中，我们一般也默认事件的发生顺序和相关性是正联系的，而相邻事件的相关性也最大，只考虑相邻事件的互相影响抓住了事物间的主要矛盾；二是非相邻事件间不是不互相影响，而是不直接影响，他们直接的相关关系通过相邻事件依次传递下去，产生了间接的影响。

        我们遇见的很多事件，如价格涨落、气候变化等都可以用马尔可夫模型进行近似。让我们从反面来理解，我举一个人造的不适合这个模型的例子：两个独立的随机事件Ai, Bi, 他们的结果混杂在了一起，如a1, b1, b2, a2, a3, b3... 这种情况下马尔可夫模型就很难进行分析。不过对于这种极端的例子，其他的分析方法恐怕也不好发挥作用，因为我们常见的时间序列类型的分析方法，大多都基于马尔可夫模型，或在其中进行一定的修改。

        因为事件间的相关关系是挨个逐次传播，像链式进行，这个模型又被称为马尔可夫链（Markov chain）。这种只与前一个事件相关的性质被成为马尔可夫性质。前一个事件与后一个事件的关联关系称为状态转移。

隐马尔可夫模型（Hidden Markov model）

 

 

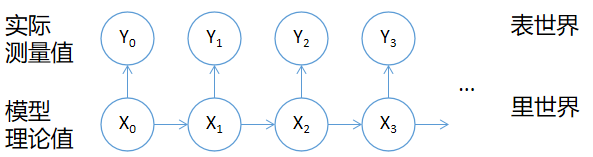
        隐马尔可夫模型是马尔可夫模型的一个深入发展：考虑到了观察和测量中误差的影响。形象的理解，我们可以看作有一个表世界和里世界，里世界就是上面提到的马尔可夫模型（理论上的离散事件Xi），而表世界里的就是对这个模型的一次次观测(Yi)。观测的结果是里世界的一个反映。这里的假设是每次观测结果Yi只与里世界对应的事件Xi有关。用条件概率来表达就是：

P(Yi | X0, X1, ...Xi, Xi+1, ...) = P(Yi | Xi) 

        还有一个有用的结论是P(... Yi-1, Yi, Yi+1,... | Xi) = P(Yi | ... Yi-1, Yi+1,... Xi) * P(... Yi-1, Yi+1,... | Xi) = P(Yi | Xi) * P(... Yi-1, Yi+1,... | Xi)，即Yi相对于其他的观测值，关于Xi条件独立。

卡尔曼滤波（Kalman filtering）

 

 

        卡尔曼滤波是一种数据处理方法，因为这种方法最早用来设计处理信号中的噪声，起到滤波改善信号的作用，所以名字中带有filter，也就是过滤噪声的意思。

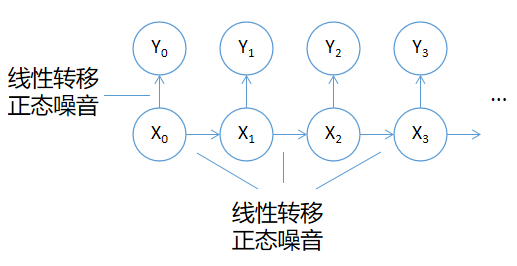
        卡尔曼滤波的方法建立在隐马尔可夫模型上，并带有更强的假设：里世界中各事件Xi间的状态转移为线性关系（即Xi的状态可由Xi-1的状态经线性组合得到），可以附带一个正态（高斯）噪音。从里世界Xi到表世界Yi的状态转移也要求是线性的，可以带一个正态（高斯）误差。用公式表达就是下面这样：

xi = Axi-1 + qi-1

yi = Hxi + ri

        其中A和H可以是矩阵（对应xi，yi为多维向量），也可以是常数（对应xi，yi为一维）。A和H代表的，就是Xi间的状态转移关系和Xi与Yi间的状态转移关系。如果要应用卡尔曼滤波，一般要求A和H，即转移关系，也就是理论模型和观测模型已知。

        qi和ri按理论要求是均值为0的正态噪音，方差一般通过估量得到。其中ri是表世界测量过程中产生的噪声，qi是里世界状态转移中的不确定性。下面我们可以看到，卡尔曼滤波是比较稳健的方法，即使qi和ri的方差估量不准确（甚至在某些情况下不满足正态分布），也往往可以收敛到正确的结果。这在一定程度上是因为卡尔曼滤波采用了类似移动平均的方法，而求平均的方法对均值为0的噪音，排除效果比较好，即使对噪音的方差或高阶矩没有好的认识。

        卡尔曼滤波的公式长这样：

xi = Axi-1 + Ki * (yi - HAxi-1) （式一）= (1 - KiH) Axi-1+ Ki * yi （式二）

        式一的形象化理解是，我先用A乘以前一项Xi-1得到一个对Xi的大致估计Axi-1，然后我再用观测值yi与估计Axi-1的差值乘一个系数，作为对大致估计误差的补偿，综合这两项得到最终估计xi。

        式二的形象化理解式，我用大致估计Axi-1和通过观测值yi反推得到实际值（Ki * yi ~ KiH * xi）做一个加权平均，一个系数为KiH，一个系数为1-KiH，平均得到最终估计。

        这两个理解本质上是等价的。因此卡尔曼滤波的实际含义就是在对里世界里的模型有一定认识的前提下，通过对系列观测数据的综合分析，滤去观测中可能存在的噪音和系统状态转移可能产生的不稳定性，得到一个相对稳定的理论值。而这也就是滤波的含义。

        上面的式子里有一个Ki，称为每一个事件的卡尔曼增益。从上面式二的形象化理解可以看出，这个增益体现的就是新的观测值能给我对实际值的估计带来多少新的信息。

Ki = Pi * H^T * (H Pi H^T + R)^-1

Pi = A Ci-1 A^T + Q

Ci = (I - Ki H) Pi

        计算Ki的公式相对较为复杂，还涉及另外两个变量Pi, 预测协方差（predict covariance），以及Ci，校正协方差（correct covariance）。其中Q、R是对噪音qi和ri的估计值。

        下面我们通过一个简单的一维例子来得到一个对这个方法更直观的理解：

i	0	1	2	3	4	5	6	7	8	9	10
xi	5.8	6.46	7.63	9.08	10.29	11.7	13.51	15.64	17.61	19.59	22.46
yi	7.18	8.323	8.19	10.69	11.9	13.08	15.94	16.88	20.19	20.84	25.20

        上面的表格中，xi间的状态转移关系为xi = 1.1 * xi-1 + qi-1，其中qi是[0, 1]间的均匀分布。

        xi到yi的转移关系是yi = 1.05 * xi + ri，其中ri是[0, 2]间的均匀分布。

        因为是一维的例子，所有矩阵均为一维，退化为一个数。A = A^T = 1.1, H = H^T =1.05

        可以看到这里的均布噪声和要求的正态噪声有一定区别，但我们可以看到卡尔曼滤波依然能取得不错的效果。

        暂估计Q = R = 1

i	0	1	2	3	4	5	6	7	8	9	10
xi（理论值）	5.8	6.46	7.63	9.08	10.29	11.7	13.51	15.64	17.61	19.59	22.46
xi（计算值）	3.59	6.47	7.56	9.54	11.04	12.35	14.63	16.08	18.7	20.1	23.35
ki	0.5	0.6	0.62	0.62	0.62	0.62	0.62	0.62	0.62	0.62	0.62
pi	1	1.58	1.72	1.72	1.72	1.72	1.72	1.72	1.72	1.72	1.72
ci	0.48	0.58	1.59	0.59	0.59	0.59	0.59	0.59	0.59	0.59	0.59

        从例子中可以看到，xi的计算值经过少量迭代即迅速逼近计算值，说明只要模型及状态转移符合要求，即使噪声估计不很准确，一样能得到稳健及有效的估计结果。

简单总结

        卡尔曼滤波是在满足以下3个条件（1，2较为重要，3在一定程度上可放松）时的，一种稳健有效的去除系统和测量误差的数据处理方法。：

1.隐马尔可夫模型；2.状态转移为线性；3.系统不确定性和测量误差满足均值为0的正态分布；