从Bellman Ford最短路径算法到Distance-Vector路由算法
最短路径算法
路由器在建立路由表的时候,需要知道到其他服务器节点的最短路径,以确定文件包的发送方式。
寻找节点间最短路径的算法就是最短路径算法。常见的最短路径算法有Dijkstra算法:对于一个节点而言,计算到其他节点的最短路径,需要知道整个网络(N个节点)的相连路径情况,再进行N次迭代计算最短路径。使用该类算法实现的路由算法称为Link-State路由算法。这类算法的基本方法是:每个节点先向其他所有节点发送本节点的路径情况:和哪些节点相连,距离是多少。待收到其他所有节点的信息后,进行一次完整的Dijkstra算法计算从本节点出发的最短路径。这类算法的好处是:路径计算过程中,迭代过程确保收敛,同时对于收到的错误路径信息能进行有效的检验(每个点都有一份完整的网络路径信息,某个节点处出现错误信息容易发现及纠正)。
然而这类算法每个节点都需要知道整个网络的路径情况,这在范围较大的公用网络中实现的代价可能比较大:如果没有像在SDN中的一个集中的全局控制器用以收集整个网络的情况,那所有节点都需要知道网络中其他所有节点的路径情况,这会带来很大的数据传输量,并使路由表的初始化过程十分缓慢。而基于Bellman Ford算法的Distance-Vector(路径向量)类路由算法可以应对这个问题。这类算法的特点是分布式实现及异步迭代更新。
Bellman Ford算法
对于一个n个节点,m条边的图,生成从节点p到其他所有节点的最短路径:
1. 初始化距离:对于目标节点p,p到自身的距离d(p)=0,到其余节点的距离d(i)初始化为无限大。
2. 进行n次迭代(或松弛relax):每次迭代中,遍历图中的每条边eij(从点i到点j),如果p到边起点i的最小距离d(i)加上边长度eij小于p到边终点的最小距离d(j),即d(i) + eij < d(j),则更新p到j的最小距离(松弛)为d(i) + eij。
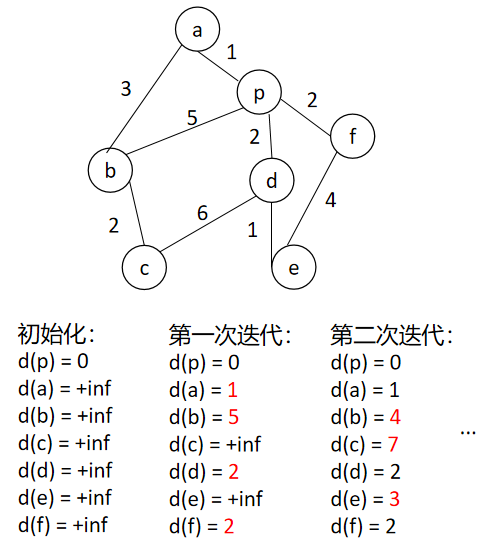
因为p到其他任意节点的最短路径最多只会通过n个节点,因此上面的n次迭代能确保找到图中存在的最短路径(即确保最后的d(i)为最小值)。
算法一共n次迭代,每次迭代都遍历所用的m条边进行距离更新,因此整个算法的时间复杂度为O(nm)。
需要注意到的是,在每次迭代中,除了更新储存的最短路径外,其余内容(图中每条边的距离)都是相对独立的,这也就给这个算法的拓展提供了空间:将算法改进为分布式异步迭代更新(每个节点计算最短路径的迭代过程按各节点情况独立进行),这就是下面要介绍的Distance-Vector算法。
Distance-Vector(路径向量)路由算法
Distance-Vector算法沿用了Bellman Ford算法的基本思想 -- Bellman Ford等式。
d(i) = min {d(j) + eij}
上面这个等式的意思是说,点p到点i的最短距离,等于这个变量的最小值:点p到任意点j的最短距离(d(j)),加上点i、点j间的距离(eij)。
这个说法可能有点绕,更直接和形象化的说法是这样:要找到点p到点i间的最短路径,分成两步 -- 1.找到这个路径的第一个(或最后一个)中间节点j。2.再找到点j和点p间的最短路径。这看起来没什么意义,但是有一个重大的作用:确定了这个路径间的一个节点j。依次迭代这样的做法,那么路径中的所用节点就都能确定了。
事实上,对路由表来说,确定这个路径的下一个节点就够了:路由器把文件转发给那个节点对应的接口就完成工作了,后面的传递由其他的路由器完成。而这种依次确定下一个节点的思想,也在强化学习(Reinforcement learning)中的Q-学习(Q-learning)中有体现。
基于这个Bellman Ford等式,就有了下面的Distance-Vector算法:
1.节点p初始化自己的距离向量(Distance Vector,也是这个算法名字的由来)-- 到各个节点的最短距离,p到自身的距离d(p)=0,到相邻节点的距离为边的长度d(i) = epi,到其余非相邻节点的距离d(i)初始化为无限大。
2. 节点p向所用相邻节点发送自己的距离向量。
3. 在收到其他节点发送的距离向量后,更新自己的距离向量。如果有变动,则重新发送自己的距离向量。一直持续这个过程。从理论上可以证明,如果网络状况是稳定的, 这个过程会收敛到最短路径。
这里我们可以看到,在整个算法的运行过程中,每个节点的距离向量(也就是路由表)都是独立持续更新的。这就保证了无论网络多大,每个路由器始终都保有一份可用的路由表,并且会根据周围节点传来的信息不断更新。这在一定程度上解决了Link-State路由算法初始化速度较慢,传送数据较多(Distance-Vector只向相邻节点发送路由表)的问题。
当然,Distance-Vector算法也有自己的问题,比如收敛到最短路径的速度会比较慢,如果网络状况出现变化,最短路径更新过程也可能比较慢。而这也是很多分布式算法会存在的问题。
最后的话
从上面我们可以看到,理论上的算法在实际应用中,可以根据不同的实际需求进行相应的改进,以适合实际的任务需求。但是改进后的算法在实际应用中的表现,仍然在很大程度上取决于原算法的理论性质。这就是算法在理论研究与实际应用中的不同的分工与侧重。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号