没初看上去那么慢的迭代加深（Iterative Deepening）搜索

　　迭代加深（Iterative Deepening）算法，对它的一般介绍多见于人工智能的算法中。但它实际上和深度优先（Depth First）与广度优先（Breadth First）一样，能应用于一般的图数据结构上。所不同的是只是它多用于图的最优路径（Optimal path）的搜索，而不是图的遍历。

　　迭代加深结合了深度优先与广度优先的特点：先设定一个初始深度值和出发节点。每次迭代，以深度值为限，开始深度优先搜索（即搜索深度到达深度值即认为到达终点，开始返回）。如果搜索到了满足条件的路径，则返回结果。如果没有找到，增进深度值，开始下一次迭代。这样在一次迭代中，使用了类似深度优先的方法，而不同次迭代间，实际上又是广度优先的方法。

（深度值=1）

（深度值=2）

（深度值=3）

　　初看起来这个算法似乎很慢：每次迭代中的搜索都必然会重复上一次迭代中的搜索结果。既然上一次的搜索没能找到正确结果，这样一再重复不是很慢吗？

　　要解决这个问题，先让我们来看看深度优先与广度优先的特点：对一个分支因子（Branching factor）为b，待搜索最优路径长度为l的图来说，广度优先的缺点在于空间复杂度达到O(b^l)，是指数级的复杂度，对于最优路径较长或分支因子较大的图不是很友好。而深度优先的缺点在于对于图中有环或者部分路径过长情况下表现不佳，因为深度优先的时间复杂度与图中最长路径的长度成指数关系，而不是与最优路径的长度成指数关系。而迭代加深则是为了避免这两种算法的缺点而被开发应用的。

　　迭代加深在每次迭代中使用的是深度优先搜索，最大空间复杂度为O(l)，是线性的复杂度。后面就让我们讨论一下看上去比较慢的时间复杂度。

　　对于深度值为k的迭代，所用时间为O(b¹ + b² + b³ + ... b^k)。

　　把深度值为1，2，3...l的迭代所用时间累加，总时间复杂度O(lb¹ + (l-1)b² + (l-2)b³ + ... + b^l)。

　　求解这个时间复杂度要用到下面这个小技巧：

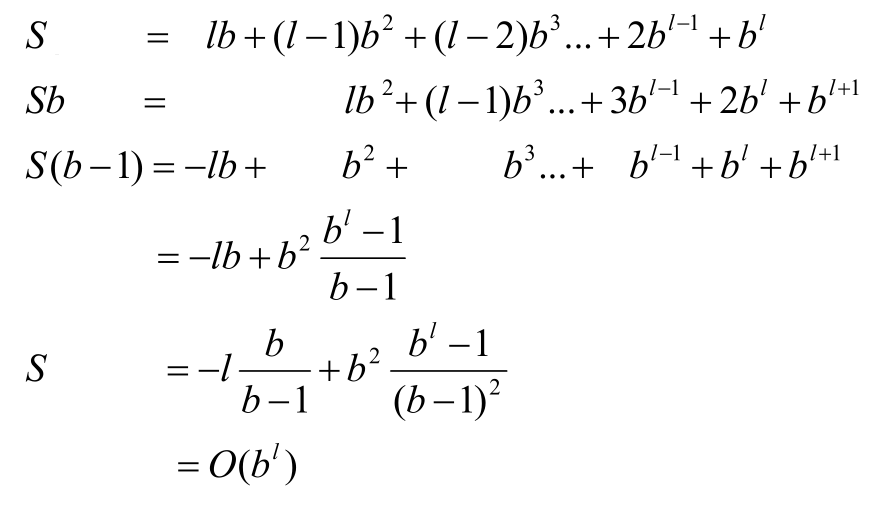
　　可以看到，迭代加深的时间复杂度为O(b^l)，虽然是指数级的复杂度，但因为是和最优路径长度成指数关系，所以这和广度优先的时间复杂度是一样。

　　也就是说，迭代加深算法用深度优先的所需空间，按广度优先的时间完成了搜索任务。：）

　　那为什么一个看上去那么慢那么笨的算法可以有这样好的表现呢？这是因为迭代加深之前的迭代虽然有很多重复的搜索，但深度值低的搜索花费的时间实际上很小，但是因为之后迭代中搜索时间按指数级增长，真正对运行时间影响大的搜索是最后一次或几次深度值最大的搜索。而迭代加深则通过重复数次深度值低的搜索，避免了深度优先搜索中可能的深度大于最优路径长度的搜索，因而显著降低了时间复杂度。