(最坏)时间复杂度,均摊时间复杂度与期望时间复杂度
(最坏)时间复杂度((worst case) time complexity)
当谈到时间复杂度(time complexity)时,我们最常用的,无明确说明默认使用的就是最坏时间复杂度(worst case time complexity)。
最坏时间复杂度考虑的是在各种数据输入情况下,一个算法所能表现出的最差执行时间界限。因为算法复杂度分析理论确保在任何情况下,算法的执行时间不会越过这个界限。所以在实际使用时,可以利用(最坏)时间复杂度对一个使用算法的程序做运行时间估计,确保在一定数据规模下,算法运行的时间不会超出我们的预期。
这是一个非常可靠的结果,因此(最坏)时间复杂度也成了我们最常用,也最好用的时间复杂度。
均摊(摊余)时间复杂度(amortized time complexity)
然而一些(最坏)时间复杂度表现不佳的算法,在实际应用中却依然有不错的表现。
比如在伸展树(Splay tree)数据结构下的查找(find)-插入(insert)-删除(delete)操作的(最坏)时间复杂度均为O(n),但实际表现并不逊色于时间复杂度为O(logn)的其他查找树。而且伸展树的实现和维护相对简单,因此也有一定的实用价值。
这种类型算法的特点是:虽然单次操作的时间复杂度较高,但是单次操作后会对整个数据的组成状况带来一定的改进,因而后续的的系列操作时间复杂度会下降。这样最坏时间复杂度就不会在系列操作中连续出现,也就使得算法的实际运行时间并没有那么糟糕。
借用一个术语,可以把这种类型算法的一个特点看做是“late(lazy) operation”。以Splay tree为例,影响查找树操作效率的关键因素是树各分枝的平衡。“平衡”的树结构操作时间复杂度较低,因而AVL tree 或 Red Black tree 都会在每次操作后对树的平衡情况进行调整,使得各个操作的时间复杂度能达到O(logn)。而Splay tree并不主动调整树的平衡,所以特殊情况下(尤其是在一些初始状态下)树可能会极不平衡,使得单次最坏时间复杂度到了O(n)。但是Splay tree在后续的操作中不断的 splay 能使树更加平衡,这样系列操作的总时间复杂度就不高了。这里的“late operation” 就是“late balance”,并不在每次操作后马上就对树结构进行平衡,而是在后续操作中根据需要逐渐balance。
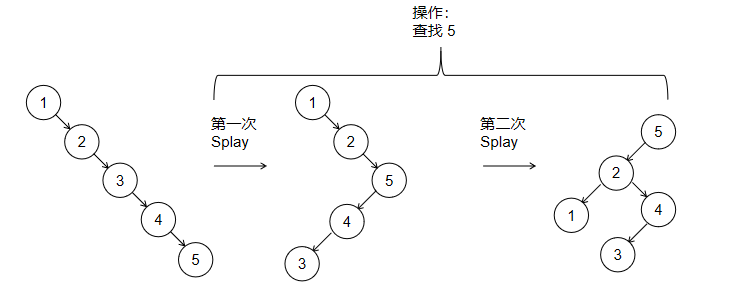
(上图中一个极不平衡的Splay树,执行一次查找操作后树的高度就减小了,变得更加平衡了。其中的秘诀在于splay使用的双旋转(zig-zag)能降低树高度。)
另外一个例子是Dynamic array,也就是变长数列。这种数列的一个实现方式是,依然采用定长数列,只是当数列中数据个数大于或小于某个界限时,重新申请一块空间来生成一个改变了长度(扩大或缩小)的数列,然后再把原数列的数据拷贝过去。这个算法的(最坏)时间复杂度为O(n),发生在需要重新生成新数列的时候。但这种情况并不会一直发生,只在数列中存储的数据规模增大或减小到一定规模时才发生,因而系列操作的时间复杂度并不高,实际使用效果也很好。这里的“late operation” 就是“late resizing array lenth”,有需要时再调整数列的储存空间。
对这类算法再以传统方式进行(最坏)时间复杂度分析明显不能反映算法的真实表现情况,因而研究者们采用均摊(摊余)时间复杂度(amortized time complexity)来处理这种情况。对均摊时间复杂度的简单理解就是把单次操作的复杂度平摊到一系列操作上,如Splay tree就是n次操作的复杂度为O(logn),单次均摊下来就是O(logn)。Dynamic array则是n次操作的复杂度为O(n),单次均摊下来就是O(1)。
均摊时间复杂度的分析方法被称为potential method,势能法。就是为数据的组成状况生成一个势能函数,通过势能函数来分析一系列操作的总体时间复杂度。一个简单的比方是重力势能函数,假如我们站在10楼,往下跳一次最多能跳10楼,但是如果跳10次,每次跳下来不往上爬的话,那这10次下来无论怎样跳一共也只能跳10楼的距离,这样均摊下来,跳一次实际上也就只跳了一层楼的高度。
再说一句,amortized均摊这个词来源于会计术语,指的也就是把单次经济活动的结果(借入或贷出)平摊到一段会计时间的做法。比方说我在618剁了手,但如果平摊到5,6,7三个月来看的话,可能每次我就只剁了一个手指头。。。而且一般情况下,无论我们剁几次手,一共也只有两只手可以剁。。。
期望时间复杂度(expected time complexity)
有些时候,我们还会发现,一些系列操作时间复杂度高的算法,也可能会有很好的运行效果。
这类算法往往就是随机性算法(Randonmized Algorithm),其中就有大名鼎鼎的快速(选择)排序(quick sort)与快速选择(quick select)。他们的特点是在特殊情况下,最坏时间复杂度和均摊时间复杂度(均摊时间复杂度也是最坏均摊时间复杂度,考虑的是系列操作最坏的情况)都不佳,就是说单次操作和系列操作都可能花费很长时间。但是这种特殊情况出现的概率非常低,以至于在实际运行中几乎不可能出现。而在一般情况下,算法又表现得非常好。。。
为了合理评价这类算法,研究人员采用了期望时间复杂度(expected time complexity),也可以说是(加权)平均时间复杂度((weighted)average time complexity)。就是说一定数据规模下,我们计算出各种数据情况出现的可能性以及相应的算法时间复杂度,将可能性和复杂度相乘后求和,就得到了期望的时间复杂度。这里的可能性如果都取相同,那就是平均时间复杂度。当然,可能性也可以根据不同的算法应用情况来确定,这样有时会得到不同的期望时间复杂度。
总的来说
(最坏)时间复杂度指的是算法单次运行可能出现的最长时间,也是最常用的时间复杂度,每次操作一定能满足。
均摊(摊余)时间复杂度指的是系列操作下最长运行时间平摊到单次操作下的均值,系列操作下的总时间一定能满足。
期望时间复杂度指的是各种数据输入下算法的运行时间按概率求得的一个平均理想值,在大多情况下能满足(实际也够用了)。。。
表面上看这几个复杂度的严格程度是一个不如一个,但实际上这是在计算机从理论走向实际大规模应用的发展。一个算法好,理论分析上专家要说好,实际应用中群众也要说好,而实际的应用场景往往会和严格理论分析下的假定有所差别。

但如果你要严格问我当提到一个算法的时间复杂度指的是哪个复杂度的时候,我只能说往往是表现最好的那个复杂度:)



