[SDOI2015]双旋转字符串 题解

Trie树+KMP做法

前置知识：Trie树 和 KMP。

---

\(\large{n=m:}\)

对于 \(n=m\) 的情况，我们只需要将每个字符串（包括 \(S,T\)）先旋转 \(n\) 次，找到其字典序最小的形态，然后将前 \(\text{TotalS}\) 个字符串放入字典树中，用后 \(\text{TotalT}\) 个字符串匹配即可。

---

\(\large{n>m:}\)

约定：设 \(S\) 集合中的字符串为字符串 \(S\)，\(T\) 集合中的字符串为 \(T\)

做法

我们设 \(len=(n+m)/2\)，然后再将每一个字符串分成 \(1\) ~ \(len\) 和 \(len+1\) ~ \(n\) 两个部分，以下图为例：

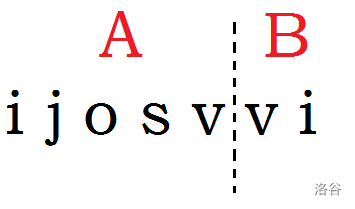
最后组成双旋转字符串时，\(A\) 是前一半字符串，\(B\) 是后一半字符串的一部分。又因为双旋转字符串的性质即后一半字符串旋转可以得到前一半字符串，所以 \(A\) 通过旋转后 \(B\) 一定可以成为 \(A\) 的子串。

根据上方结论，可以得到 \(B\) 一定是字符串 \(AA\) 的子串。如图所示：

然后我们在 \(AA\) 上匹配 \(B\)，匹配到的第一个（想想看为什么是第一个） \(B\) 的后 \(m\) 个字符所组成的字符串就是这个 \(S\) 所对应的 \(T\) 了。

最后拿 Trie树 匹配即可。

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=4000010;
int n,m,S,T,len,ans=0;
string a[maxn];
string b;
int trie[maxn][26],tag[maxn],cnt=1;
int kmp[maxn];
void insert(string s)//Trie树操作
{
	register int x=1;
	for(register int i=0;i<s.length();i++)
		if(trie[x][s[i]-'a']) x=trie[x][s[i]-'a'];
		else trie[x][s[i]-'a']=++cnt,x=cnt;
	tag[x]++; 
}
void work(string s)//Trie树操作
{
	register int x=1;
	for(register int i=0;i<s.length();i++)
		x=trie[x][s[i]-'a'];
	ans+=tag[x];
}
string MIN(string s)
{
	char c;
	string ans="%";
	for(register int i=1;i<=len;i++)
	//旋转 len 次，得到字典序最小的形态
		c=s[0],s.erase(s.begin()),s.insert(s.end(),c),ans=(ans=="%")?s:min(s,ans);
	return ans;
}
int main()
{
	cin>>S>>T>>n>>m,len=(n+m)/2;
	if(n==m)//特判 n=m 的情况
	{
		string s;
		for(register int i=1;i<=S;i++)
			cin>>s,insert(MIN(s));
		for(register int i=1;i<=T;i++)
			cin>>s,work(MIN(s));
		cout<<ans<<endl;
		return 0;
	}
	register char c;
	for(register int t=1;t<=S;t++)
	{
		a[t]="$",b="$";//加上 $ 方便从 1 计数
		for(register int i=1;i<=len;i++)
			cin>>c,a[t]+=c;
		for(register int i=1;i<=len;i++)
			a[t]+=a[t][i];//将字符串 A 写成 AA
		for(register int i=len+1;i<=n;i++)
			cin>>c,a[t]+=c,b+=c;//再读入读入后面 B 的一部分
		//以下为KMP
		register int j=0;
		for(register int i=2;i<=n-len;i++)
		{
			while(j&&b[i]!=b[j+1]) j=kmp[j];
			if(b[i]==b[j+1]) j++;
			kmp[i]=j; 
		}
		j=0;
		for(register int i=1;i<=n+len;i++)
		{
			while(j&&a[t][i]!=b[j+1]) j=kmp[j];
			if(a[t][i]==b[j+1]) j++;
			if(j==n-len)
			{
				if(i>len+len) break;
				string s;
				//匹配上后,将i的后m位插入 trie 树(即 S 可以匹配的T)
				for(register int u=i+1;u<=i+m;u++)
					s+=a[t][u];
				insert(s);
				break;
			}
		}
	}
	string s;
	for(register int i=1;i<=T;i++)
		cin>>s,work(s);
	cout<<ans<<endl;
	return 0;
}