[NOI 2021] 轻重边 题解

提供一种和不太一样的树剖解法（一下考场就会做了qwq），尽量详细讲解。

思路

设重边为黑色，轻边为白色。

首先，先将边的染色转化为点的染色（即将 \(u\) 节点连向父节点的边的颜色转化为 \(u\) 节点的颜色）。

对于操作一，如果要把涉及到的点全部染色，显然是不现实的。设染成颜色 \(1\) 的路径为 \(x,y\)，便容易得到一个结论：

除了 \(\text{LCA(x,y)}\) 会被染成白色以外，所有被染成白色的节点都是路径上节点的子节点。

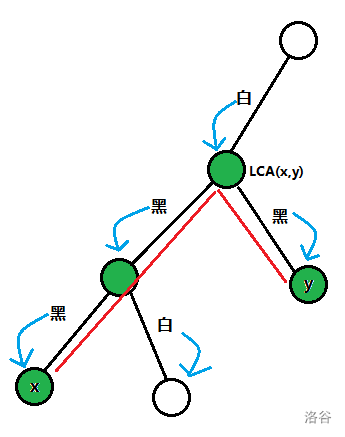
可以结合上图理解一下。

也就是说，只要对于每个操作 \(1\) 给 \(\text{LCA(x,y)}\) 染成白色，以及给整个链的其他部分染上黑色，每个节点的颜色就只和节点本身与其父节点相关了。

此外，后来的操作会影响先前的操作，所以对于每个节点，我们需要存储下每个节点最后被覆盖成黑色的时间以及被覆盖成白色的时间，然后这个东西看起来好像就可以用线段树来维护了。

实现方式

在实现过程中，其实还有好多好多的问题要处理，这里详细讲一下实现方法。

• 边权转点权

  将边权转化为点权后，点 \(\text{LCA(x,y)}\) 虽然不用染成黑色，但是其子节点是需要被染成白色的（可以结合上文的图辅助理解）。对于这种特殊情况，我们要同时将 \(\text{LCA(x,y)}\) 染成黑色和白色（非常离奇），也就是把黑色和白色的时间戳都更新成同一个时间。这样处理后，仍然可以根据父节点和节点本身来判断一个节点的颜色（见下文）。

• 判断节点颜色(重点)

  关键点来了，如何判断一个节点的颜色？

  设父节点为 \(A\)，子节点为 \(B\)。

  1.最后一次是染 \(A\) 且不是染 \(B\)

  且不是B 代表在染 \(B\) 的同时，没有染 \(A\)（这可不是废话哦）。根据后来操作覆盖先前操作，\(B\) 的颜色完全取决于 \(A\)。而根据染色的方式，只要是染色的节点，一定处于染黑的链上（即使是点 \(\text{LCA(x,y)}\) 也没关系，因为其子节点也要被染白），所以 \(B\) 一定是白色。

  2.最后一次是染黑 \(B\) 且不是染白 \(B\)。

  这里不需要考虑染 \(B\) 的同时有没有染 \(A\)，因为 \(B\) 的优先级更高（考虑 \(A\) 相当于是间接染，考虑 \(B\) 相当于是直接染，按照操作优先级可知）。

  \(B\) 在染成黑色的链上且不是 \(\text{LCA(x,y)}\)，一定是黑色。

  3.最后一次是染黑 \(B\) 且也是染白 \(B\)

  说明 \(B\) 是 \(\text{LCA(x,y)}\)，一定是白色。

在代码实现中，只需要判最后一次 是染黑 \(B\) 且不是染白 \(B\) 是否成立就好了。

• 线段树维护细节

  为了处理区间合并，每个节点应该存储的信息有：

  \(\text{l}_0,\text{l}_1,\text{r}_0,\text{r}_1,\text{data}\)

  即左端点最后一次被染成白色的时间、被染成黑色的时间，右端点最后一次被染成白色的时间、被染成黑色的时间，区间黑色点数量。这样便可以处理区间合并时的边界问题了。

  另外，由于 \(i\) 的颜色与 \(i-1\)（指 \(dfn\) 序）的相关，所以 \([l,r]\) 只能维护 \([l+1,r]\) 内的黑色点数量！ 因此，在处理每个区间的黑色点数量时，还需要特殊处理左边界是否为黑色点。

代码

常数很大，\(960ms\) 卡过去了。

#include<bits/stdc++.h>
#define pb push_back
using namespace std;
const int maxn=100010;
inline int read()
{
	register int x=0;
	register char c=getchar();
	for(;!(c>='0'&&c<='9');c=getchar());
	for(;c>='0'&&c<='9';c=getchar())
		x=(x<<1)+(x<<3)+(c&15);
	return x;
}
int T;
int n,m,cnt,head[maxn],Cnt;
int fa[maxn],d[maxn],dfn[maxn],top[maxn],zson[maxn];
struct node
{
	int u,v,to;
}e[maxn<<1];
void addedge(int u,int v)
{
	e[++Cnt].u=u,e[Cnt].v=v;
	e[Cnt].to=head[u],head[u]=Cnt;
}
struct tree
{
	int l,r,data;
	int lt[2],rt[2],lz[2];
}a[maxn*3];
void build(int i,int l,int r)
{
	if(l>r) return ;
	a[i].l=l,a[i].r=r;
	a[i].data=0;
	a[i].lt[0]=a[i].rt[0]=1;
	a[i].lt[1]=a[i].rt[1]=0;
	a[i].lz[0]=a[i].lz[1]=0;
	//因为有多组数据，所以0也要赋值。
	if(l==r) return ;
	register int mid=(l+r)>>1;
	build(i<<1,l,mid),build(i<<1|1,mid+1,r);	
}
void pushdown(int i)
{
	if(!a[i].lz[1]) return ;
	a[i<<1].lz[1]=a[i<<1|1].lz[1]=a[i].lz[1];
	a[i<<1].lt[1]=a[i<<1].rt[1]=a[i].lz[1];
	a[i<<1|1].lt[1]=a[i<<1|1].rt[1]=a[i].lz[1];
	a[i<<1].data=a[i<<1].r-a[i<<1].l;
	a[i<<1|1].data=a[i<<1|1].r-a[i<<1|1].l;
	a[i].lz[1]=0;
}
void add(int i,int l,int r,bool col,int time)
//将[l,r]区间最后一次染成col的时间覆盖为time
{
	if(a[i].l>=l&&a[i].r<=r)
	{
		a[i].lt[col]=a[i].rt[col]=time;
		a[i].data=(col?a[i].r-a[i].l:0);
		a[i].lz[col]=time;
		return ;
	}
	if(a[i].l>r||a[i].r<l) return ;
	pushdown(i);
	add(i<<1,l,r,col,time),add(i<<1|1,l,r,col,time);
	a[i].lt[col]=a[i<<1].lt[col],a[i].rt[col]=a[i<<1|1].rt[col];
	register int Max=max(max(a[i<<1].rt[0],a[i<<1].rt[1]),max(a[i<<1|1].lt[0],a[i<<1|1].lt[1]));
	a[i].data=a[i<<1].data+a[i<<1|1].data+(Max==a[i<<1|1].lt[1]&&Max!=a[i<<1|1].lt[0]);
	//特判区间的边界
}
int getsum(int i,int l,int r)
//[l+1,r]内黑点数量
{
	if(a[i].l>=l&&a[i].r<=r) return a[i].data;
	if(a[i].l>r||a[i].r<l) return -1;
	pushdown(i);
	register int x,y;
	x=getsum(i<<1,l,r),y=getsum(i<<1|1,l,r);
	if(x==-1) return y;
	if(y==-1) return x;
	register int Max=max(max(a[i<<1].rt[0],a[i<<1].rt[1]),max(a[i<<1|1].lt[0],a[i<<1|1].lt[1]));
	return x+y+(Max==a[i<<1|1].lt[1]&&Max!=a[i<<1|1].lt[0]);
}
pair<int,int> getime(int i,int x)
//返回x位置上的点最后一次被染成白,黑色的时间
{
	if(a[i].l==a[i].r)
		return make_pair(a[i].lt[0],a[i].lt[1]);
	pushdown(i);
	if(a[i<<1].r>=x) return getime(i<<1,x);
	else return getime(i<<1|1,x);
}
//以下dfs是树剖
int dfs1(int fath,int x)
{
	fa[x]=fath,d[x]=d[fa[x]]+1,zson[x]=0;
	register int Max=-1,sum=1,xx;
	for(register int u=head[x];u;u=e[u].to)
		if(e[u].v!=fa[x])
		{
			xx=dfs1(x,e[u].v),sum+=xx;
			if(xx>Max) Max=xx,zson[x]=e[u].v;
		}
	return sum;
}
void dfs2(int x)
{
	dfn[x]=++cnt;
	if(zson[fa[x]]==x) top[x]=top[fa[x]];
	else top[x]=x;
	if(zson[x]) dfs2(zson[x]);
	for(register int u=head[x];u;u=e[u].to)
		if(e[u].v!=fa[x]&&e[u].v!=zson[x])
			dfs2(e[u].v);
}
void work(int time,int x,int y)
//将x到y的路径染成黑色
{
	while(top[x]!=top[y])
		if(d[top[x]]>d[top[y]])
			add(1,dfn[top[x]],dfn[x],1,time),x=fa[top[x]];
		else
			add(1,dfn[top[y]],dfn[y],1,time),y=fa[top[y]];
	if(d[x]>d[y]) 
		add(1,dfn[y],dfn[x],1,time),add(1,dfn[y],dfn[y],0,time);
	else
		add(1,dfn[x],dfn[y],1,time),add(1,dfn[x],dfn[x],0,time);
	//别忘了将LCA再染成白色
}
pair<int,int>tt,t;
int solve(int x,int y)
//求x到y路径上黑色点数量
{
	register int sum=0,X,XX,Y,YY,Max;
	while(top[x]!=top[y])
		if(d[top[x]]>d[top[y]])
		{
			t=getime(1,dfn[top[x]]),tt=getime(1,dfn[fa[top[x]]]);
			X=t.first,XX=t.second;
			Y=tt.first,YY=tt.second;
			Max=max(max(X,XX),max(Y,YY));
			sum+=getsum(1,dfn[top[x]],dfn[x])+(Max==XX&&Max!=X);
			//别忘了额外处理边界(即'(Max==XX&&Max!=X)')
			x=fa[top[x]];
		}
		else
		{
			t=getime(1,dfn[top[y]]),tt=getime(1,dfn[fa[top[y]]]);
			X=t.first,XX=t.second;
			Y=tt.first,YY=tt.second;
			Max=max(max(X,XX),max(Y,YY));
			sum+=getsum(1,dfn[top[y]],dfn[y])+(Max==XX&&Max!=X);
			//别忘了额外处理边界(即'(Max==XX&&Max!=X)')
			y=fa[top[y]];
		}
	if(d[x]==d[y])
		return sum;		
	if(d[x]>d[y])
	{
		y=zson[y];
		t=getime(1,dfn[y]),tt=getime(1,dfn[fa[y]]);
		X=t.first,XX=t.second;
		Y=tt.first,YY=tt.second;
		Max=max(max(X,XX),max(Y,YY));
		sum+=getsum(1,dfn[y],dfn[x])+(Max==XX&&Max!=X);
	}
	else
	{
		x=zson[x];
		t=getime(1,dfn[x]),tt=getime(1,dfn[fa[x]]);
		X=t.first,XX=t.second;
		Y=tt.first,YY=tt.second;
		Max=max(max(X,XX),max(Y,YY));
		sum+=getsum(1,dfn[x],dfn[y])+(Max==XX&&Max!=X);
	}
	return sum;	
}
int main()
{
	T=read();
	while(T--)
	{
		memset(head,0,sizeof(head));
		cnt=0,Cnt=0;
		n=read(),m=read();
		register int x,y,z,opt;
		for(register int i=1;i<n;i++)
			x=read(),y=read(),addedge(x,y),addedge(y,x);
		dfs1(0,1),dfs2(1),build(1,1,n);
		register int M=m+1;
		for(register int i=2;i<=M;i++)
		{
			opt=read(),x=read(),y=read();
			if(opt==1) work(i,x,y);
			else printf("%d\n",solve(x,y));
		}
	}
	return 0;
}

完结撒花～～

如果有什么问题欢迎在评论区或者私信提出哦！