[NOI Online 2021 入门组] 吃豆人题解
思路
首先可以发现,任何一个吃豆人路线都一定会经过四条边。因此,我们可以通过枚举第一行上的点来确定吃豆人路线(不重不漏)。两个吃豆人,时间复杂度 \(O(n^2)\)。
接下来就是如何 \(O(1)\) 求值的问题了。
我们可以维护一个扭曲的前缀和,设 \(p[i]\) 表示经过 \((1,i)\) 的那一个唯一吃豆人路线所能吃到的豆子数的总和,那么对于点 \((x,y)\),会对以下两个前缀和有贡献:
- 经过以下处理后的 \(p[y]\):
- 经过以下处理后的 \(p[y]\):
解释:
\(min(x-1,y-1)\):向左上方最多走的步数。
\(min(x-1,n-y)\):向右上方最多走的步数。
(由于要回到第一行,所以不考虑向下)
也就是说,一种是先向左上方走到底后再往右上方走
另一种是则相反。
(这里画画图就明白了,一个点最多只会对两个前缀和有贡献)
这样,这道题就完成了 \(50\%\) 了。
难点
(至少对我是的)
下一个问题就是,两个吃豆人路线可能会有交点,按照容斥原理,还要减去交点处。那么,如何求交点呢?
以下图为例(\(y>x\)):
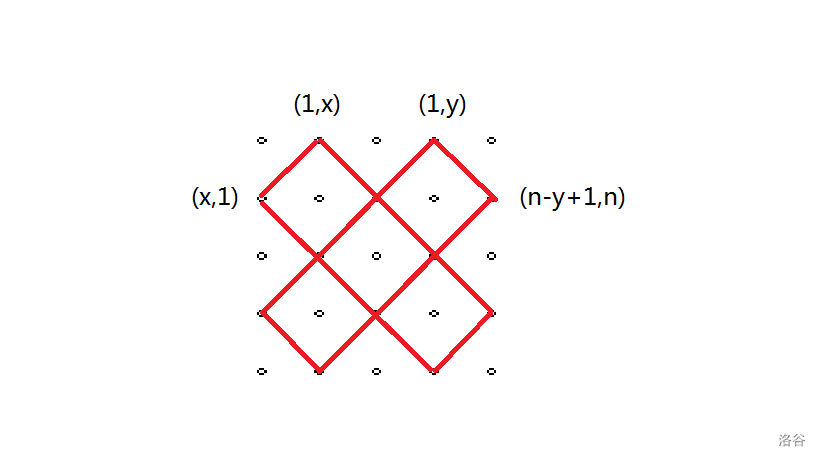
可以发现,两个矩阵会有四个焦点,分别是 \((x,1)(1,y)\),\((1,x)(1,y)\),\((n-y+1,n)(x,1)\),\((n-y+1,n)(x,1)\) 这四组坐标向下 \(45\) 度的线段的交点。
以 \((n-y+1,n)(1,x)\) 为例:
我们设 \((1,x)\) 向下经过的第 \(k\) 个点与 \((n-y+1,n)\) 向下经过的第 \(kk\) 个点重合,那么按照 \(x,y\) 坐标相等,可以列出二元一次方程组:
解得 \(kk=\frac{x+y-2}{2}\)。
同理可以求出剩下的交点。
这里需要注意的有两点:
-
如果 \(y-x\) 是奇数,那么它们没有交点;
-
如果 \(x=1\) 或者 \(y=n\),那么交点数会相应得减少(上图的点重合),要特判。
接下来看代码就好啦。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=1010;
inline int read()
{
register int x=0;
register char c=getchar();
for(;!(c>='0'&&c<='9');c=getchar());
for(;c>='0'&&c<='9';c=getchar())
x=(x<<1)+(x<<3)+c-'0';
return x;
}
int ans;
int a[maxn][maxn],n;
int p[maxn];
int jiao(int x,int y)
{
//上文推导
if((y-x)&1) return 0;
register int sum=0,kk;
kk=(y-x)>>1;
sum+=a[1+kk][y-kk];
if(y!=n)
sum+=a[1+n-y+kk][n-kk];
if(x!=1)
{
kk=(x+y-2)>>1;
sum+=a[1+kk][y-kk];
if(y!=n)
sum+=a[1+n-y+kk][n-kk];
}
return sum;
}
int main()
{
n=read();
int x,y,xx,yy,sb;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
a[i][j]=read();
//处理前缀和
x=i,y=j;
sb=min(x-1,n-y),x-=sb,y+=sb;
sb=min(x-1,y-1),x-=sb,y-=sb;
p[y]+=a[i][j];
xx=i,yy=j;
sb=min(xx-1,yy-1),xx-=sb,yy-=sb;
sb=min(xx-1,n-yy),xx-=sb,yy+=sb;
if(yy!=y)
p[yy]+=a[i][j];
}
if(n==1)
//特判n=1,因为下面利用贪心的思想让 i≠j,这对于 n=1 是不成立的。
{
cout<<a[1][1]<<endl;
return 0;
}
for(register int i=1;i<=n;i++)
for(register int j=i+1;j<=n;j++)
ans=max(ans,p[i]+p[j]-jiao(i,j));
cout<<ans<<endl;
return 0;
}

