线代学习笔记(使用:线性代数 李炯生)(后面水了,开始用川大教材)
多项式
第一章怎么是多项式,不知道为什么,学了但是先不做笔记了。
行列式
(以下称第 \(i\) 位为 \(1\) 其他位为 \(0\) 的向量为 \(\epsilon_i\))
\(k\) 重线性函数

(我的理解是,对每一位都线性变化的函数)
反对称
\(k\) 个向量中存在相同时函数值为 \(0\) 的函数为“反对称”。
同时“反对称”也同时拥有该性质:将任意两个向量交换位置,则函数值反号。
“规范的”
若 \(f(\epsilon_1,\cdots,\epsilon_n)=1\) 则称 \(f()\) 为“规范的”。
行列式
\(n\) 重“线性”“反对称”“规范的”函数就是行列式。(其中我们把每行看做一个向量)
至此我们可以得到行列式的一些重要性质:
- 交换任意两行则变号(反对称性)
- 两行成比例则行列式为 \(0\)
- 把某行减去另一行的任意倍,行列式不变(线性性和反对称性)
- 转置前后行列式不变(由后边算法推出)(因此行列式中行与列地位等同,性质相同)
行列式的算法:
-
通过代数余子式递归;
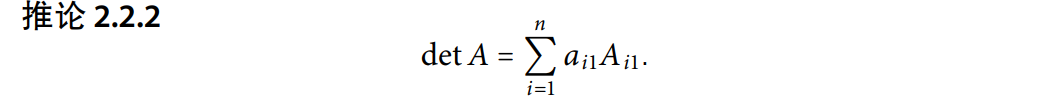
-
各种排列取点乘逆序对数(该证明只需要把所有向量都完全拆掉,再用线性性拉出来变成系数,只留下单位向量在函数中):

子式和余子式
子式指取出某 \(p\) 行 \(p\) 列的重合项出来排成的新矩阵。
余子式指一个子式子选的那些行列去掉后,得到的新矩阵。
代数余子式指余子式乘上 \((-1)^k\) (其中 \(k\) 代表去掉的行列编号和)
拉普拉斯展开


证明思路可以由“各行取点”来得到。指定 \(p\) 行后,我们首先把这 \(p\) 行换到最上面,然后取遍每种 \(p\) 列(即这 \(p\) 行只取这 \(p\) 列含的值),作为“上部矩阵”的元素,剩下作为下部矩阵元素。那么把这 \(p\) 列移到最左后,因为我们上部只取前 \(p\) 列,下部只取后 \(p\) 列,那么一定不取的地方可以替换为 \(0\) 则变成前一个图的情况,最终得证。
(普通用代数余子式递归到 \((n-1)^2\) 矩阵的计算方法就是拉普拉斯展开 \(p=1\) 时的特例。)
一个小定理
一行的数配对另一行的代数余子式,和为 \(0\) ,证明:这样算等于算另一个矩阵的行列式,这个矩阵形如 把代数余子式去掉的行替换成作为系数的那行,于是两行系数一样,故为 \(0\).

cramer法则


实际上这个方法一般不好用,但是至少了解一下,说不定什么时候可能用上吧。
常用行列式计算方法
- 消成主对角线矩阵。
- 建立递推式,或者说递归到小行列式。
- 用拉普拉斯展开
- 加边,把矩阵扩大,然后通过消元什么的变好算

- 拆行(列),根据线性性,把某一行拆为两个向量的和,把矩阵分成两个好算的。
- 把一个元看成未定元列出多项式(确定次数和根),最后求出最高次系数。

矩阵
- 矩阵的加法是各位相加,和行列式不一样。
- 矩阵的数乘是各位乘这个数,和行列式不一样。
- 矩阵可以把某些矩形部分合并来进行计算,即变成以矩阵为元素的矩阵,各种运算结果和展开时候的完全一样。
(向量左成矩阵时候,其实可以把矩阵每一列看做一个基向量,然后对原本向量做基变换)
矩阵乘法

(矩阵重要就重要在乘法上)。
矩阵乘法满足结合律,但是不满足交换律与消去律。
矩阵转置
转置展开时候,记得内部乘法倒过来 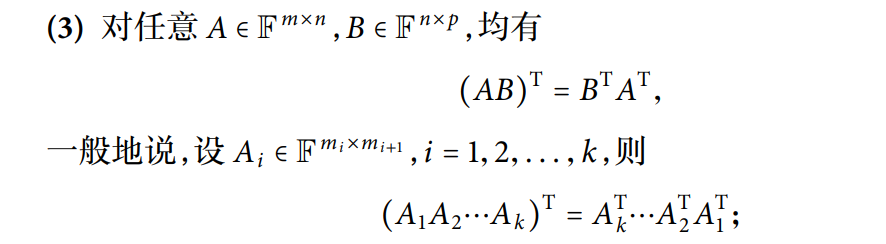
Binet-Cauchy 定理
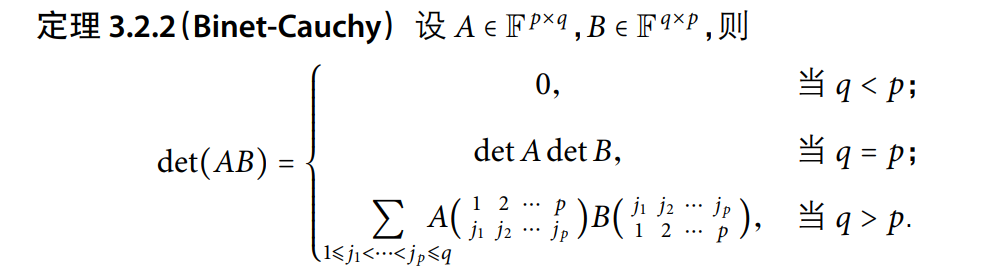
(后两个其实等价,第一个是因为一定有空列)
矩阵的逆
- 行列式不为 \(0\) 的方阵都有逆,且为伴随矩阵除行列式(当然求的时候可以用别的方法求,比如列线性方程组然后高消,或者直接右边加一个单位矩阵然后一起消)
- 矩阵的逆唯一
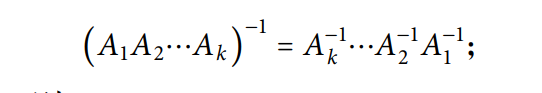
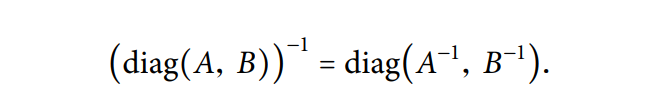
矩阵打洞

小结论
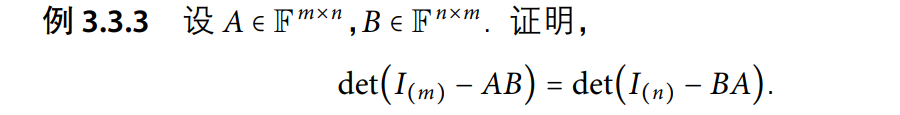
有时候原本难算的 \(AB\) 可以变成好算的 \(BA\) (如直接变成一个数)
矩阵的秩
最少有几个基,秩就多大。同秩且同大小的矩阵相抵。
相抵指两个矩阵通过初等变换可以变成同一个。
各种初等变换都可以表示为矩阵,称作初等矩阵。
矩阵有逆 等同于 矩阵可以表示为若干初等矩阵的积。
秩为 \(r\) 说明至少有一个 \(r\) 阶主子式满秩。
线性方程组
线性齐次方程组的解空间:

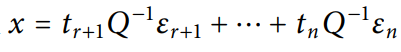
更一般地,对于非齐次的:
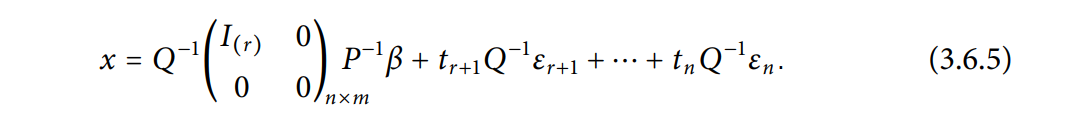
线性方程有解的情况

挺显然的,因为秩如果不变说明与前面线性相关,有解;否则无解。
前面的定理看起来解决了问题,却没有具体方法,实际操作办法其实还是高消。
矩阵的广义逆
水水水
线性空间


这里“加法”和“乘法”可以指代任意运算。

线性空间的同构



子空间
水水水
直和

商空间

书打错了:\(W\) 是 \(V\) 的子空间。

这些同余类加法和数乘都容易定义。(即取代表元进行,然后得到结果所在的同余类)
\(W\) 的补和 \(V/W\) 同构,可以构造双射证明。
象与核

映射为 \(0\) 的是核。
\(\text{Im}()\) 和 \(\text{Ker}()\) 分别是 \(\text{V}\) 和 \(\text{U}\) 的子空间。




线性变换

\(B\) 变换其实可以直接看成把:基,通过 \(\text{P}\) 变到另一种 基下,然后再进行 \(A\) 变换,最后再通过 \(\text{P}^{-1}\) 变回到原本的基下。
不变子空间

特征向量特征值






