codeforces 919E Congruence Equation

E. Congruence Equation
time limit per test
3 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

Given an integer x. Your task is to find out how many positive integers n (1 ≤ n ≤ x) satisfy

where a, b, p are all known constants.
Input

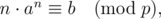
The only line contains four integers a, b, p, x (2 ≤ p ≤ 106 + 3, 1 ≤ a, b < p, 1 ≤ x ≤ 1012). It is guaranteed that p is a prime.

Output

Print a single integer: the number of possible answers n.

Examples
input
2 3 5 8
output
2
input
4 6 7 13
output
1
input
233 233 10007 1
output
1
Note

In the first sample, we can see that n = 2 and n = 8 are possible answers.

 

 

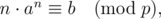
大意：求使上式成立的n的数量(1<=n<=x)

 

题解：看了tag才有了灵感：

 

n*a^n≡b(mod p)

可以变形为

n%p*a^(n%(p-1))≡b(mod p)         ——费马小定理和同余原理

令n%p= i , n%(p-1)=j.

可以倒过来考虑，对于一组使同余方程成立的 i 和 j ，求有多少个n。

 

枚举 j，解方程求出 i ，然后求最小的 n ，易得n+k*(p-1)*p也是合法的解(k为任意自然数)。

解方程求出 i 应该不用讲了，求出最小的n以后算出这组 i , j 贡献的答案数也不难。（细节可以见代码）

最大的问题是如何解出n

中国剩余定理！

想要求n，可以做如下变形：

n≡ i (mod p)

n≡ j (mod p-1)

可以用中国剩余定理来求解。

推荐中国剩余定理讲解：

https://www.cnblogs.com/MashiroSky/p/5918158.html

 

最后一个小细节：p等于2的时候用费马小定理求逆元会出现问题，特判，如果是exgcd求逆元应该不会碰到这个问题。

 1 /*
 2 Welcome Hacking
 3 Wish You High Rating
 4 */
 5 #include<iostream>
 6 #include<cstdio>
 7 #include<cstring>
 8 #include<ctime>
 9 #include<cstdlib>
10 #include<algorithm>
11 #include<cmath>
12 #include<string>
13 using namespace std;
14 int read(){
15     int xx=0,ff=1;char ch=getchar();
16     while(ch>'9'||ch<'0'){if(ch=='-')ff=-1;ch=getchar();}
17     while(ch>='0'&&ch<='9'){xx=(xx<<3)+(xx<<1)+ch-'0';ch=getchar();}
18     return xx*ff;
19 }
20 long long READ(){
21     long long xx=0,ff=1;char ch=getchar();
22     while(ch>'9'||ch<'0'){if(ch=='-')ff=-1;ch=getchar();}
23     while(ch>='0'&&ch<='9'){xx=(xx<<3)+(xx<<1)+ch-'0';ch=getchar();}
24     return xx*ff;
25 }
26 int mypow(int x,int p,int MOD){
27     int re=1;
28     while(p){
29         if(p&1)
30             re=1LL*re*x%MOD;
31         p>>=1;
32         x=1LL*x*x%MOD;
33     }
34     return re;
35 }
36 int a,b,p;
37 long long x,ans;
38 int main(){
39     //freopen("in","r",stdin);
40     a=read(),b=read(),p=read();
41     x=READ();
42     if(p==2){
43         cout<<x/2+(x%2==1)<<endl;
44         return 0;
45     }
46     long long mul=1LL*p*(p-1);
47     for(int i=0;i<=p-2;i++){
48         int y=1LL*b*mypow(mypow(a,i,p),p-2,p)%p;
49         long long temp=(1LL*i*p*mypow(p,p-3,p-1)%mul+1LL*y*(p-1)*mypow(p-1,p-2,p)%mul)%mul;
50         ans+=x/mul+(x%mul>=temp);
51     }
52     cout<<ans<<endl;
53     return 0;
54 }
View Code

 

 

 

 

posted @ 2018-02-01 20:14  咸鱼lzh  阅读(356)  评论(0)  编辑  收藏  举报