codeforces 918D MADMAX

 

D. MADMAX

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

As we all know, Max is the best video game player among her friends. Her friends were so jealous of hers, that they created an actual game just to prove that she's not the best at games. The game is played on a directed acyclic graph (a DAG) with n vertices and m edges. There's a character written on each edge, a lowercase English letter.

Max and Lucas are playing the game. Max goes first, then Lucas, then Max again and so on. Each player has a marble, initially located at some vertex. Each player in his/her turn should move his/her marble along some edge (a player can move the marble from vertex v to vertex u if there's an outgoing edge from v to u). If the player moves his/her marble from vertex v to vertex u, the "character" of that round is the character written on the edge from v to u. There's one additional rule; the ASCII code of character of round i should be greater than or equal to the ASCII code of character of round i - 1 (for i > 1). The rounds are numbered for both players together, i. e. Max goes in odd numbers, Lucas goes in even numbers. The player that can't make a move loses the game. The marbles may be at the same vertex at the same time.

Since the game could take a while and Lucas and Max have to focus on finding Dart, they don't have time to play. So they asked you, if they both play optimally, who wins the game?

You have to determine the winner of the game for all initial positions of the marbles.

Input

The first line of input contains two integers n and m (2 ≤ n ≤ 100, ).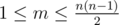

The next m lines contain the edges. Each line contains two integers v, u and a lowercase English letter c, meaning there's an edge from v to u written c on it (1 ≤ v, u ≤ n, v ≠ u). There's at most one edge between any pair of vertices. It is guaranteed that the graph is acyclic.

Output

Print n lines, a string of length n in each one. The j-th character in i-th line should be 'A' if Max will win the game in case her marble is initially at vertex i and Lucas's marble is initially at vertex j, and 'B' otherwise.

Examples

input

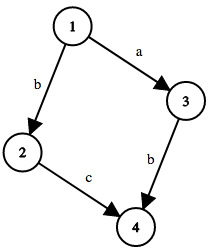
4 4
1 2 b
1 3 a
2 4 c
3 4 b

output

BAAA
ABAA
BBBA
BBBB

input

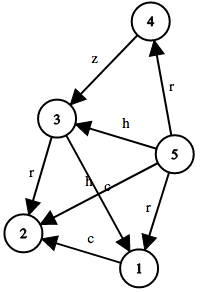
5 8
5 3 h
1 2 c
3 1 c
3 2 r
5 1 r
4 3 z
5 4 r
5 2 h

output

BABBB
BBBBB
AABBB
AAABA
AAAAB

Note

Here's the graph in the first sample test case:

Here's the graph in the second sample test case:

 

大意：在一个有向无环图上，两个人分别从一个点出发，两人轮流从当前点沿着某条边移动，要求经过的边权不小于上一轮对方经过的边权（ASCII码），如果一方不能移动，则判负。两人都采取最优策略，求两人分别从每个点出发的胜负关系表。

 

题解：记忆化搜索。

f[x][y][v]表示现在两人分别在x,y，上一轮经过的边权为v时x是否能胜利（胜利为1，失败为0）。

考虑如何转移：

对于一条从x到u的边权为val的边，如果val>=v，则可以走这条边，算出f[y][u][val]，

如果f[y][u][val]为0，则说明在   f[x][y][v]这个状态下，有使得x胜利的方案，因为两个玩家都采取最优策略，这时x必定获胜。f[x][y][v]=1

如果f[y][u][val]为1，不要紧，主动权现在在处于x点的玩家手中，他可以不从这条路走，继续考察下一条x的出边。

如果无论如何处于x的玩家都赢不了，那么f[x][y][v]=0。

 

/*
Welcome Hacking
Wish You High Rating
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
using namespace std;
int read(){
    int xx=0,ff=1;char ch=getchar();
    while(ch>'9'||ch<'0'){if(ch=='-')ff=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){xx=(xx<<3)+(xx<<1)+ch-'0';ch=getchar();}
    return xx*ff;
}
const int maxn=105;
int N,M,lin[maxn],len;
struct edge{
    int y,next,v;
}e[maxn*maxn];
inline void insert(int xx,int yy,int vv){
    e[++len].next=lin[xx];
    lin[xx]=len;
    e[len].y=yy;
    e[len].v=vv;
}
int f[maxn][maxn][26];
int dfs(int x,int y,int v){
    if(f[x][y][v]!=-1)
        return f[x][y][v];
    f[x][y][v]=0;
    for(int i=lin[x];i;i=e[i].next)
        if(e[i].v>=v)
            if(!dfs(y,e[i].y,e[i].v)){
                f[x][y][v]=1;
                break;
            }
    return f[x][y][v];

}
int main(){
    //freopen("in.txt","r",stdin);
    memset(f,-1,sizeof(f));
    N=read(),M=read();
    for(int i=1;i<=M;i++){
        int t1=read(),t2=read(),t=getchar()-'a';
        insert(t1,t2,t);
    }
    for(int i=1;i<=N;i++){
        for(int j=1;j<=N;j++)
            if(dfs(i,j,0))
                printf("A");
            else
                printf("B");
        puts("");
    }
    return 0;
}