K最近邻算法
K最近邻（K-Nearest-Neighbour,KNN）算法是机器学习里简单易掌握的一个算法。通过你的邻居判断你的类型，“近朱者赤，近墨者黑”表达了K近邻的算法思想。
一．算法描述：
1.1 KNN算法的原理
KNN算法的前提是存在一个样本的数据集，每一个样本都有自己的标签，表明自己的类型。现在有一个新的未知的数据，需要判断它的类型。那么通过计算新未知数据与已有的数据集中每一个样本的距离，然后按照从近到远排序。取前K个最近距离的样本，来判断新数据的类型。
通过两个例子来说明KNN算法的原理
（1）下图中，绿色圆要被决定赋予哪个类，是红色三角形还是蓝色四方形？如果K=3，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类，如果K=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。
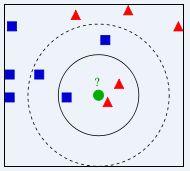
从该图中可以看出K值的选取对类别的判断具有较大的影响，K的选择目前没有很好的办法，经验规则K值一般低于训练样本的开平方。
（2）有六部已知类型的电影，有人统计了电影场景中打斗次数和接吻次数，如下表。最后一行表示有一部新的电影，统计了其中打斗和接吻的次数，那么如何判断这部电影是爱情片还是动作片。
|
电影名称 |
打斗次数 |
接吻次数 |
电影类型 |
|
California Man
|
3 |
104 |
Romance |
|
He’s Not Really into Dudes
|
2 |
100 |
Romance |
|
Beautiful Woman
|
1 |
81 |
Romance |
|
Kevin Longblade
|
101 |
10 |
Action |
|
Robo Slayer 3000
|
99 |
5 |
Action |
|
Amped II
|
98 |
2 |
Action |
|
未知 |
18 |
90 |
Unknown |
将打斗次数和接吻次数分别作为x,y轴，得到下图
？表示未知电影的未知，然后计算该位置到其他点的距离，假定K=3，可知，距离最近都是爱情片，因此判定该电影也是爱情片。
1.2 KNN算法的优缺点
该算法在分类时有个主要的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。因此可以采用权值的方法（和该样本距离小的邻居权值大）来改进。
该方法的另一个不足之处是计算量较大，因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。
1.3 算法执行步骤：
（1）生成向量位置
（2）计算样本集到新数据的距离
（3）对样本集按距离进行排序
（4）根据K选取样本，判定类型
二．Python实现
1.简单实现
创建数据集并实现knn算法
#knn agorithm*** #2014-1-28 *** from numpy import import operator def createDataSet(): group=array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]]) labels=['A','A','B','B'] return group,labels def classify0(inX,dataSet,labels,k): dataSetSize=dataSet.shape[0] diffMat=tile(inX,(dataSetSize,1))-dataSet ddMat=diffMat**2 dsumMat=sum(ddMat,axis=1) deqrMat=dsumMat**0.5 sortMat=deqrMat.argsort() dic={} for i in range(k): lab=labels[sortMat[i]] dic[lab]=dic.get(lab,0)+1 maxlabelcout=sorted(dic.iteritems(),key=operator.itemgetter(1),reverse=True) return maxlabelcout[0][0]
对测试数据进行类型判断
#knn ********* #run the knn1 with [0,0]**** #2014-1-28 ********* #zhen ********* import knn1 group,labels=knn1.createDataSet() print group print labels g=knn1.classify0([0,0],group,labels,3) print g
2.实际应用-约会网站
###knn agorithm ###2014-1-28 from numpy import * import operator #knn def classify0(inX,dataSet,labels,k): dataSetSize=dataSet.shape[0] diffMat=tile(inX,(dataSetSize,1))-dataSet ddMat=diffMat**2 dsumMat=sum(ddMat,axis=1) deqrMat=dsumMat**0.5 sortMat=deqrMat.argsort() dic={} for i in range(k): lab=labels[sortMat[i]] dic[lab]=dic.get(lab,0)+1 maxlabelcout=sorted(dic.iteritems(),key=operator.itemgetter(1),reverse=True) return maxlabelcout[0][0] def fileopen(filename): f=open(filename) flines=f.readlines() fsize=len(flines) index=0 mat=zeros((fsize,3)) labels=[] for line in flines: line=line.strip() list=line.split('\t') mat[index,:]=list[0:3] labels.append(int(list[-1])) index+=1 return mat,labels def autonorm(Dataset): dmin=Dataset.min(0) dmax=Dataset.max(0) ranges=dmax-dmin datanorm=zeros(shape(Dataset)) m=Dataset.shape[0] datanorm=Dataset-tile(dmin,(m,1)) datanorm=datanorm/tile(ranges,(m,1)) return datanorm,ranges,dmin def classTest(): hoRatio=0.1 mat,lables=fileopen('datingTestSet2.txt') dataNorm,ranges,dmin=autonorm(mat) m=mat.shape[0] numTest=int(m*hoRatio) errorCount=0.0 for i in range(numTest): lablesTest=classify0(dataNorm[i,:],dataNorm[numTest:m,:],\ lables[numTest:m],3) if (lablesTest!=lables[i]): errorCount+=1.0 print "the classifier came back with:%d,the real answer is:%d"\ %(lablesTest,lables[i]) print "the total error rate is: %f" % (errorCount/numTest) def classifyperson(): resultTypeList=['not at all','in small doses','in large doses'] percentGame=float(raw_input(\ "percentage of time spent playing video games?")) miles=float(raw_input("miles earned per year?")) iceCream=float(raw_input("liters of ice cream per year?")) mat,lables=fileopen('datingTestSet2.txt') dataNorm,ranges,dmin=autonorm(mat) arr=array([miles,percentGame,iceCream]) result=classify0((arr-dmin)/ranges,dataNorm,lables,3) print "You will probably like this person: ",\ resultTypeList[result-1]
3.手写识别
