OO第一单元总结——表达式求导
第一次作业
(1) UML结构图
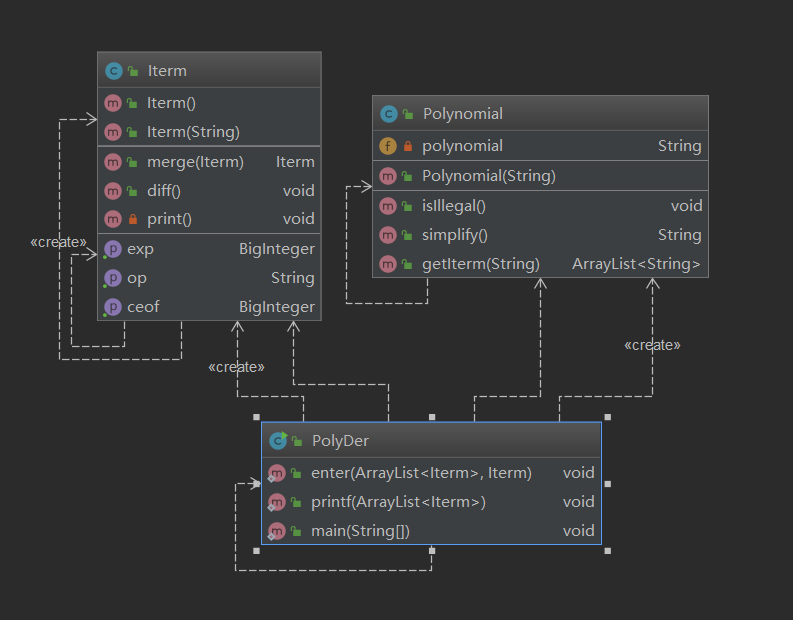
(2)结构分析
Polynomial 类是对输入的字符串进行预处理,其中包括判断格式是否合法,运算符简化,分割成项等方法。
Polynomial处理后得到的每一个项的字符串,传给Iterm类(这个类名是item和term的组合,互测中独一无二的类名,真是可怕!),iterm类通过构造函数获取各个信息。iterm类还有实现求导的方法,以及生成合并同类项的方法。
PolyDer类没有属性,只有enter(Arraylist 添加对象)方法,和print方法。
(3)耦合度分析
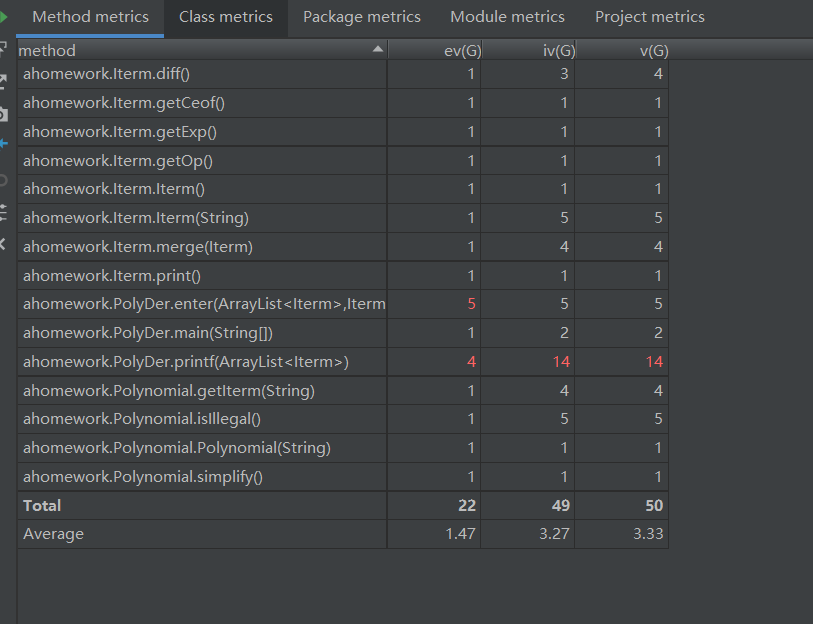
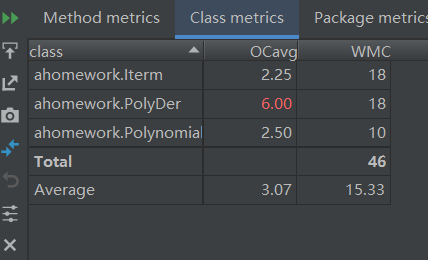
PolyDer中,print方法以及enter方法复杂度高,写的比较面向过程。尤其是print方法有待改进。改进方法可在iterm类中写一个成员方法print,按要求输出该项。然后只需在main函数中的for循环下,调用每个对象的print方法即可。
(4)难点分析
第一次作业的难点在于正则表达式解析字符串。一开始我是用大正则匹配整项的,后来发现存在爆栈的风险就做了改进。利用项的几个基本形式,对表达式挨个项匹配。
(5)BUG分析
自己:
第一次作业比较庆幸,强测互测都没有被找到bug,不过优化忘了将正项提前,所以也不是满分。
同屋:
感觉强测还是很弱的……
bug集中在两个地方:
(1)关于 结果为0的一些输入上(大概大家对这个0的输出优化条件并没有考虑周全)
比如 0 ,+x-x,……
(2)格式错误
在OO之前,我们很少考虑程序的鲁棒性。但是这种什么错误输入都有的情况才更贴切实际。这次作业很多人的bug出在\v,\f等上
第二次作业
(1)UML结构图
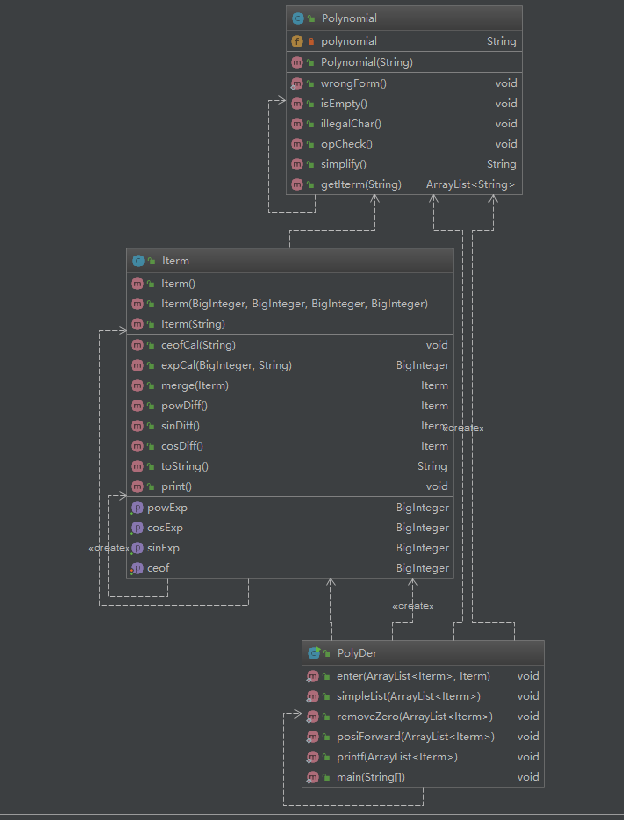
(2)结构分析
这次我的结构和第一次是差不多的,只是Iterm类增加了几个属性。每个项都可表示为 系数*幂函数*三角函数的形式。Iterm类中也增加了sin和cos的求导方法。除此之外,相比于第一次作业的print部分,这是有在Iterm类中写了一个toString方法。
PolyDer类是个比较杂糅的类,我把优化的各种方法(简单的合并同类项,sin(x)^2+cos(x)^2=1的化简,正项提前等)都写在了这里面。
(3)耦合度分析
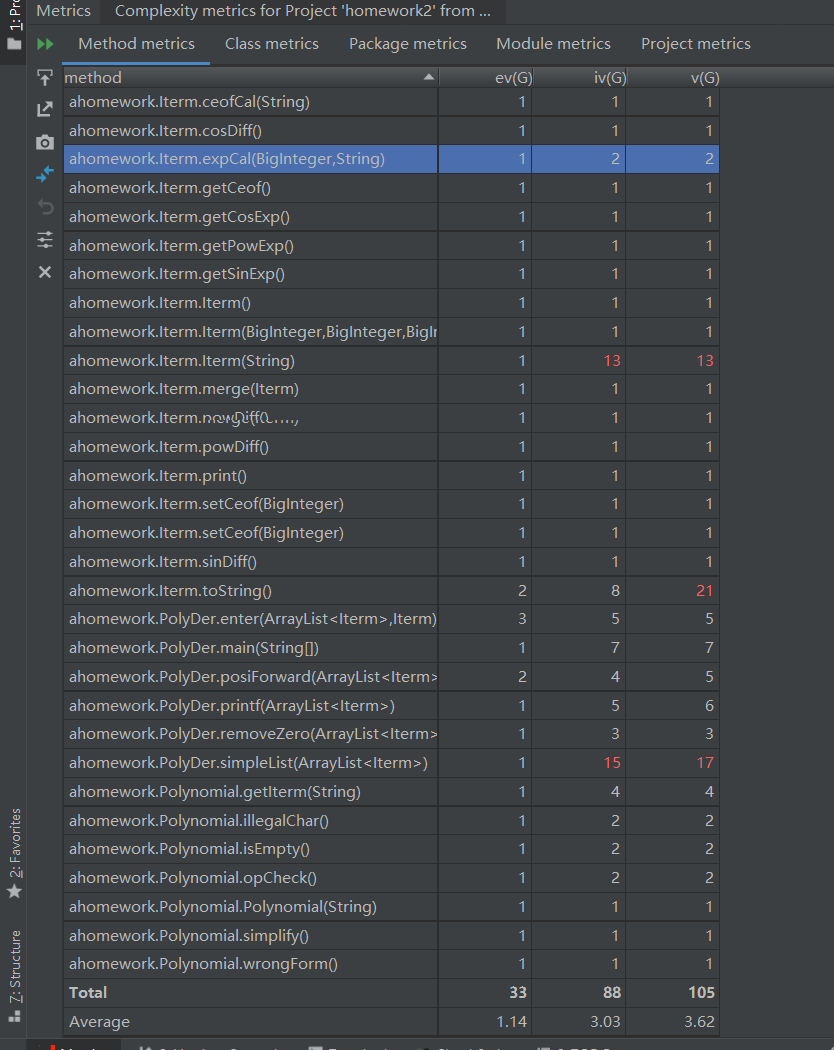
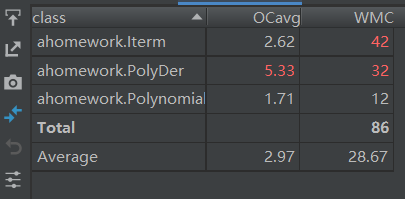
不是很高明的结构,三次嵌套的循环等导致这次的我的优化部分尤其是simpeList方法的耦合度和复杂度都比较高。还有,Iterm的构造函数既提取信息又检验格式,耦合度和复杂度也很高。
(4)BUG分析
自己的BUG
+ - 号位置不同导致的数量多变的关系,其中还有很多与空格、*的组合关系。这让我从表达式中分割出项的时候忘考虑了*后面也可以有+-号,因此强测卡了三个点(心痛……)。
同屋的BUG
这次的BUG中 ,还是集中在WF和优化方面。
错误格式比如1*-sin(x),1*--1等
(5)Applying Creational Pattern
对于我的sin(x)^2+cos(x)^2=1的化简,应该是比较充分的,但是没有用什么高明的算法,实现方式比较蠢笨。
反复遍历ArrayList,直到上一次没有化简(sin(x)^2+cos(x)^2=1处理后的两项toString的长度和比之前小则算作一次化简)终止循环。
研讨课上大佬介绍了启发式化简,运用的结构是treeMap。感觉很高明,正在研究……
第三次作业
(1)UML结构图
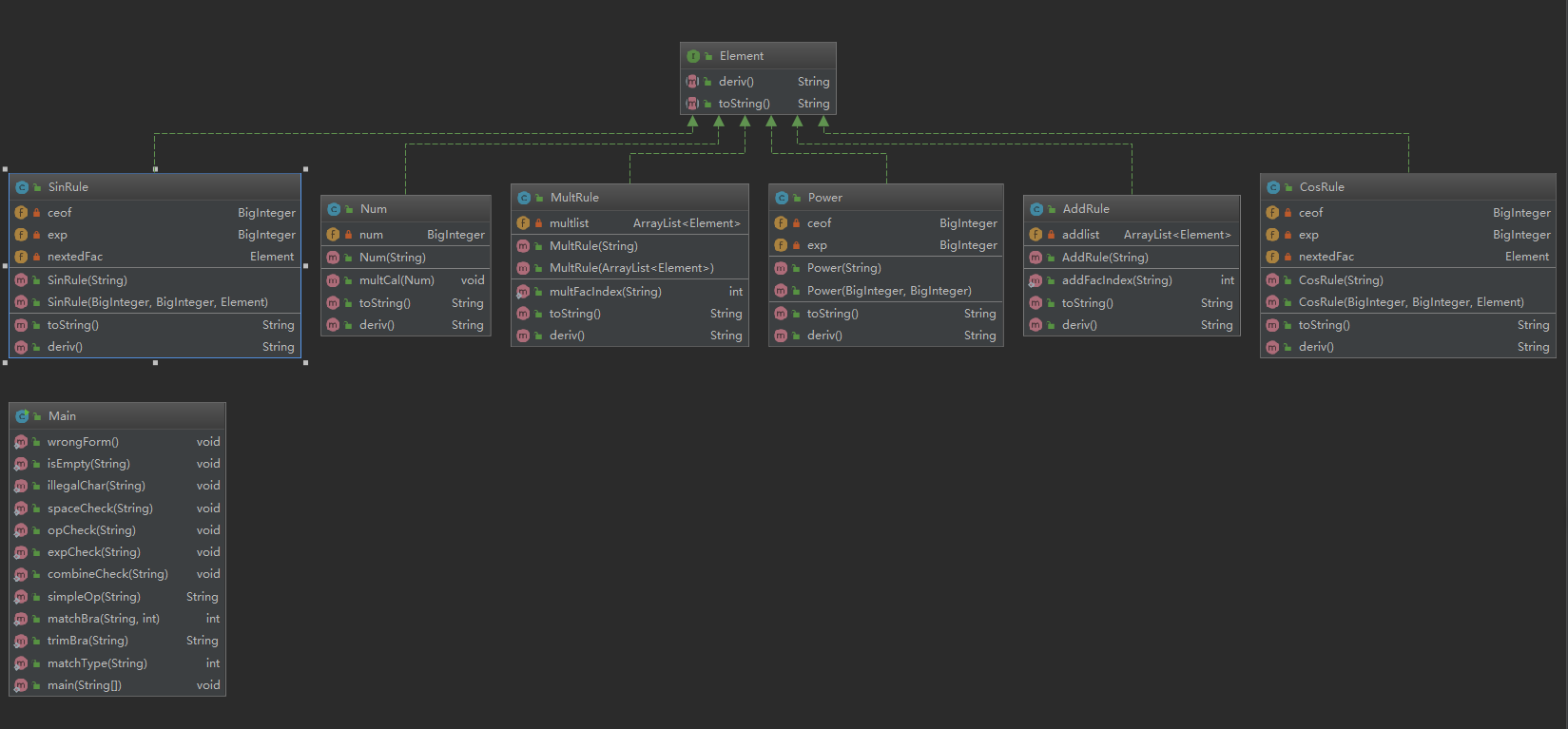
(2)结构分析
这次作业第一次尝试使用接口。写了四个最小单元类(常数类,幂函数类,sin类,cos类),两个运算类(乘法类,加法类)
表达式字符串传给加法类的构造函数,然后加法类分解各个项,传至其他五个类。其中乘法类也对字符串进行分解,将各个因子传给四个最小单元类,表达式因子传给加法类。
至于提取各个部分,我并没有用正则的方法,而是用了匹配的括号进行分割,这个比较面向过程,有待改进……
(3)耦合度分析

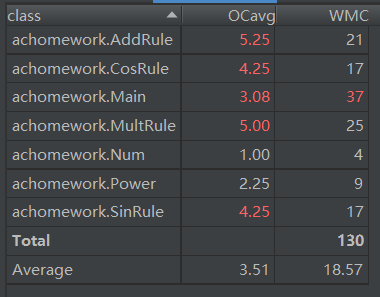
就每个方法来说的话,其实耦合度和复杂度都还好。
但对每个类来说,复杂度比较高。我把格式判断与提取信息全放在构造函数里,实在是太菜了!我要学习!
(4)难点分析
a.表达式的提取。递归下降啊,其实我也不知道自己写的是不是递归下降……
b.优化。这很大程度上取决于工程采取的结构。这次我没有刻意的去优化,只去除了多余的外围括号……
(5)BUG分析
自己:
庆幸强测互测都没被hack,不过也多亏互测不给测试错误格式的数据。其实我的代码是有bug的(暗喜)
同屋的BUG:
这次我有尝试用脚本,可以同时输出同屋所有人的输出。当然一对比,有的人很强,做了很多优化,有的人却很长很长……可以看出,一个屋的实力差距还是蛮大的。也惊奇地发现,有的人的代码在处理加法的时候会更短,有的人是乘法,有的人是嵌套。这大概和每个人采取的结构有很大关系。
至于bug,我只找到了两个。一个是0*0*0*0*0*0*0*0……(没输出),还有一个是(((((……(x)……)))))的嵌套(爆栈了)。
(6)Applying Creational Pattern
我将字符串分解依次往下传到构造函数中,虽是递归,却很不“文明”。应该采取真正的递归下降的算法。
其实实现简单的优化还是可以的,比如同底数因子的合并,以及同类项的加减合并。只需我每个基类里写上同类、同底数的方法。然后在加法类加入项的时候有序,并且合并同类项;在乘法类加入因子的时候有序,然后同底的化简即可。


