2019.3.13 Java实现分数的四则运算
Java实现分数的四则运算
自己的写法
markdown太久没写格式不会用了--将就着看
- Fraction.java
package com.lanou;
public class Fraction {
private int numerator1; //定义属性:分子1
private int denominator1; //定义属性:分母1
private String operator; //定义属性:运算符
private int numerator2; //定义属性:分子2
private int denominator2; //定义属性:分母2
//构造方法
//constructor生成
public Fraction(int numerator1, int denominator1, String operator, int numerator2, int denominator2) {
this.numerator1 = numerator1;
this.denominator1 = denominator1;
this.operator = operator;
this.numerator2 = numerator2;
this.denominator2 = denominator2;
}
//加法
public void addition() {
int x = numerator1 * denominator2 + numerator2 * denominator1;
int y = denominator1 * denominator2;
gcd(x,y);
}
//减法
public void subtraction() {
int x = numerator1 * denominator2 - numerator2 * denominator1;
int y = denominator1 * denominator2;
gcd(x,y);
}
//乘法
public void multiplication(){
int x = numerator1 * numerator2;
int y = denominator1 * denominator2;
gcd(x,y);
}
//除法
public void division(){
int x = numerator1 * denominator2;
int y = denominator1 * numerator2;
gcd(x,y);
}
//欧几里得+判断输出
public int gcd(int m,int n) {
//定义四个空变量
int r;
int t;
int u;
int w;
//t和w用来存储分子和分母的初始数据
t = m;
w = n;
//求最大公因数
while (n != 0) {
r = m % n;
m = n;
n = r;
}
//循环结束后此时m即为最大公因数
//放个u = m看着方便
u = m;
//分子分母分别除以最大公因数
t = t / u;
w = w / u;
//判断+输出
//分子分母都为1 直接输出1
if(t == 1 && w == 1){
System.out.println("1");
}
//分子为0 分母不为0 直接输出0
else if(t == 0 && w != 0){
System.out.println("0");
}
//分子分母都不为0且不为1 直接输出
else {
System.out.println(t + "/" + w);
}
return 0;
}
}
- MainClass.java
package com.lanou;
import java.util.Scanner;
public class MainClass {
public static void main(String[] args) {
System.out.println("请输入按分子1分母1运算符分子2分母2的形式输入数据");
Scanner scanner = new Scanner(System.in);
int a = scanner.nextInt();
int b = scanner.nextInt();
String o = scanner.next();
int c = scanner.nextInt();
int d = scanner.nextInt();
//判断分母是否为0 若为0重新输入 不为0继续判断
if (b == 0 || d == 0){
System.out.println("分母不能为零,请重新输入");
a = scanner.nextInt();
b = scanner.nextInt();
o = scanner.next();
c = scanner.nextInt();
d = scanner.nextInt();
}
//判断o中是否是运算符
if (!o.equals("+") && !o.equals("-") && !o.equals("*") && !o.equals("/")){
System.out.println("运算符输入错误,请重新输入");
a = scanner.nextInt();
b = scanner.nextInt();
o = scanner.next();
c = scanner.nextInt();
d = scanner.nextInt();
}
Fraction fraction = new Fraction(a, b, o, c, d);
if (o.equals("+")){
fraction.addition();
}
else if (o.equals("-")){
fraction.subtraction();
}
else if (o.equals("*")){
fraction.multiplication();
}
else if (o.equals("/")){
fraction.division();
}
}
}
大仁哥的写法
/**
* @author lizhongren1.
*/
public class Fraction {
// 分子(numerator)
private int ntNum;
// 分母(Denominator)
private int doNum;
// 构造方法, 这里没写空的构造方法, 换句话说就是要求必须要有分子和分母.
public Fraction(int ntNum, int doNum) {
this.ntNum = ntNum;
this.doNum = doNum;
if (doNum == 0){
// 分母不能为0
System.out.println("分母不能为0, 已经改为1");
this.doNum = 1;
}
// 创建新分数之后进行约分处理
reduce();
}
// 分数加法
public Fraction add(Fraction f){
// a/b + c/d
// 生成新的分子: a * d + b * c
int newNt = ntNum * f.getDoNum() + doNum * f.getNtNum();
// 生成新的分母: b * d
int newDo = doNum * f.getDoNum();
// 使用新的分子分母创建一个新的分数对象
Fraction newF = new Fraction(newNt, newDo);
return newF;
}
// 约分方法: 把分数化为最简分数, 即 6/12 化为 1/2
// 此方法和下一个方法都不想让外部调用, 因此设置为private
private void reduce(){
// 获得最大公约数
int m = maxDe(ntNum, doNum);
ntNum = ntNum / m;
doNum = doNum / m;
}
// 最大公约数: 使用辗转相除法(又名欧几里德算法, 别问我怎么来的, 去问欧几里德)
private int maxDe(int a, int b){
while(b != 0)
{
int r = a % b;
a = b;
b = r;
}
return a;
}
// 输出字符串, 按照 分子/分母的形式输出
@Override
public String toString() {
// 分子为0时输出0
if (ntNum == 0){
return "0";
}
// 分子分母相同时输出1
if (ntNum == doNum){
return "1";
}
// 其余方式按 分子/分母 输出
return ntNum + "/" + doNum;
}
// getter/setter方法
public int getNtNum() {
return ntNum;
}
public void setNtNum(int ntNum) {
this.ntNum = ntNum;
}
public int getDoNum() {
return doNum;
}
public void setDoNum(int doNum) {
this.doNum = doNum;
}
// main方法测试
public static void main(String[] args) {
Fraction f1 = new Fraction(1,3);
Fraction f2 = new Fraction(4,9);
// 分数f1 加上 分数f2
Fraction nf = f1.add(f2);
System.out.println(nf);
System.out.println(nf.add(new Fraction(9,12)));
}
}
-
输入与输出
-
测试数据
-
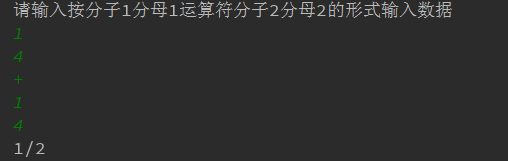
输入格式:分子1 回车 分母1 回车 运算符 回车 分子2 回车 分母2 回车
-
1/4+1/4
-
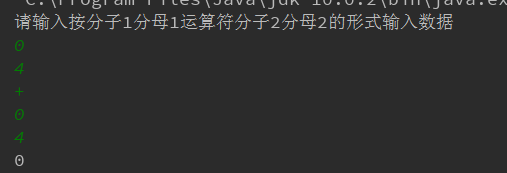
0/4+0/4
-
4/0+4/0



