最长公共子序列和最长公共子串(dp)
现在已经开始做动态规划的题目了,挂一个老师布置的作业
最长公共子序列和最长公共子串都是dp的经典题目
具体问题网上都有很多变形,接下来我先介绍一下最原始的问题:
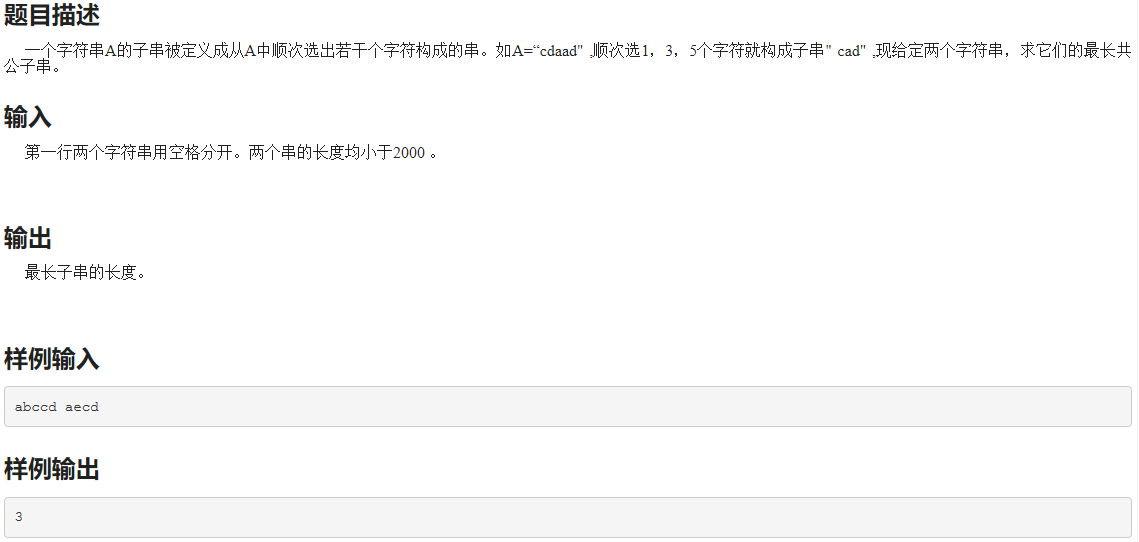
该题就是最为典型的最长公共子序列。子序列与下面要讲的子串的不同之处是:子序列中的字符在原串中不一定连续,但是字母的相对位置没有改变,而子串则是一个连续的原串的子集。
我们可以使用动态规划的方法解决这两个问题:
1.最长公共子序列(LCS)
设X=x1x2…xm和Y=y1y2…yn是两个序列,Z=z1z2…zk是这两个序列的一个最长公共子序列。
1. 如果xm=yn,那么zk=xm=yn,且Zk-1是Xm-1,Yn-1的一个最长公共子序列;
2. 如果xm≠yn,那么zk≠xm,意味着Z是Xm-1,Y的一个最长公共子序列;
3. 如果xm≠yn,那么zk≠yn,意味着Z是X,Yn-1的一个最长公共子序列。
我们使用dp[i][j]来表示第一个串的前i位和第二个串的前j位中的最长公共子序列,我们很容易能发现当两个串的任意一个串的当前长度为0时,它的最长公共子序列的长度为0,所以先对dp数组的边界进行初始化。然后我们发现,如果a[i]=b[j],dp[i][j]=dp[i-1][j-1]+1,很显然,当比对的位字符一样时,能得到该状态转移方程。如果a[i]≠b[j],dp[i][j]=max(dp[i-1][j],dp[i][j-1]),该状态转移方程是由上面的2,3条取最大值得到的。
下面看一下代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 int dp[2005][2005]; 4 int main() 5 { 6 char a[2005],b[2005]; 7 cin>>a>>b; 8 for(int i=0;i<=strlen(a);i++) 9 { 10 dp[i][0]=0; 11 } 12 for(int j=0;j<=strlen(b);j++) 13 { 14 dp[0][j]=0; 15 } 16 for(int i=1;i<=strlen(a);i++) 17 { 18 for(int j=1;j<=strlen(b);j++) 19 { 20 if(a[i-1]==b[j-1]) 21 { 22 dp[i][j]=dp[i-1][j-1]+1; 23 } 24 else 25 { 26 dp[i][j]=max(dp[i-1][j],dp[i][j-1]); 27 } 28 } 29 } 30 cout<<dp[strlen(a)][strlen(b)]<<endl; 31 return 0; 32 }
2.最长公共子串

这就是最长公共子串的基本概念,和子序列非常像,但是字串是要求连续的。我们使用dp[i][j]来表示第一个串的前i位和第二个串的前j位中的最长公共子串,我们很容易能发现当两个串的任意一个串的当前长度为0时,它的最长公共子序列的长度为0,所以先对dp数组的边界进行初始化。然后我们发现,如果a[i]=b[j],dp[i][j]=dp[i-1][j-1]+1,很显然,当比对的位字符一样时,能得到该状态转移方程。如果a[i]≠b[j],dp[i][j]=0,说明无论之前有没有连续的子串,到了这个不相等的位置会直接断掉,所以dp[i][j]=0;
下面是最长公共子串的代码:
#include<bits/stdc++.h> using namespace std; int dp[2005][2005]; int main() { char a[2005],b[2005]; cin>>a>>b; for(int i=0;i<=strlen(a);i++) { dp[i][0]=0; } for(int j=0;j<=strlen(b);j++) { dp[0][j]=0; } for(int i=1;i<=strlen(a);i++) { for(int j=1;j<=strlen(b);j++) { if(a[i-1]==b[j-1]) { dp[i][j]=dp[i-1][j-1]+1; } else { dp[i][j]=0; } } } int maxn=-1; for(int i=1;i<=strlen(a);i++) { for(int j=1;j<=strlen(b);j++) { maxn=max(maxn,dp[i][j]); } } cout<<maxn<<endl; return 0; }



