[LeetCode 1697] Checking Existence of Edge Length Limited Paths

An undirected graph of n nodes is defined by edgeList, where edgeList[i] = [ui, vi, disi] denotes an edge between nodes ui and vi with distance disi. Note that there may be multiple edges between two nodes.

Given an array queries, where queries[j] = [pj, qj, limitj], your task is to determine for each queries[j] whether there is a path between pj and qj such that each edge on the path has a distance strictly less than limitj .

Return a boolean array answer, where answer.length == queries.length and the jth value of answer is true if there is a path for queries[j] is true, and false otherwise.

 

Example 1:

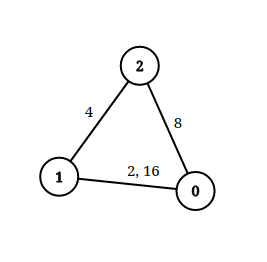
Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
Output: [false,true]
Explanation: The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.

Example 2:

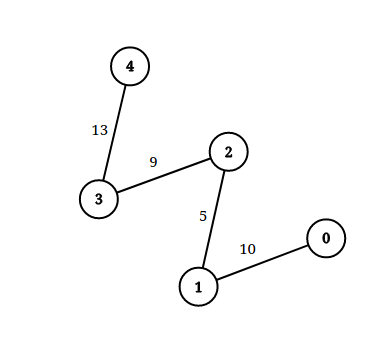
Input: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
Output: [true,false]
Exaplanation: The above figure shows the given graph.

 

Constraints:

• 2 <= n <= 105
• 1 <= edgeList.length, queries.length <= 105
• edgeList[i].length == 3
• queries[j].length == 3
• 0 <= ui, vi, pj, qj <= n - 1
• ui != vi
• pj != qj
• 1 <= disi, limitj <= 109
• There may be multiple edges between two nodes.

 

The key observation here is that this problem requires an offline algorithm. That is, all the queries are given at once. This means we do not have to process each query in order, as long as we return the correct answer for each query, we are good. So we can process all the queries by its edge length limit in ascending order. For each bigger limit, connect all the new available edges that fit in this limit. For dynamic graph connectivity problem, Union Find is a good option.

 

1.  Sort all queries by their edge limits, appending query index.

2. Sort all edges by their weights in ascending order.

3. For each query, if there are new available edges that can be added to the current graph using Union Find, add them. Then check the answer of the current query.

 

class Solution {
    class UnionFind {
        int[] id;   //parent link
        int[] sz;  //size of component for roots

        UnionFind(int N) {
            this.id = new int[N];
            this.sz = new int[N];
            for(int i = 0; i < N; i++) {
                this.id[i] = i;
                this.sz[i] = 1;
            }
        }
        boolean connected(int p, int q) {
            return find(p) == find(q);
        }
        
        int find(int p) {
            if(p != this.id[p]) {
                this.id[p] = find(this.id[p]);
            }
            return this.id[p];
        }

        void union(int p, int q) {
            int i = find(p);
            int j = find(q);
            if(i == j) {
                return;
            }

            if(this.sz[i] < this.sz[j]) {
                this.id[i] = j;
                this.sz[j] += this.sz[i];
            }
            else {
                this.id[j] = i;
                this.sz[i] += this.sz[j];
            }
        }
    }
    public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {
        int m = queries.length;
        int[][] q = new int[m][2];
        for(int i = 0; i < m; i++) {
            q[i][0] = queries[i][2];
            q[i][1] = i;
        }
        Arrays.sort(q, Comparator.comparingInt(e->e[0]));
        UnionFind uf = new UnionFind(n);
        boolean[] ans = new boolean[m];
        Arrays.sort(edgeList, Comparator.comparingInt(e->e[2]));
        
        int j = 0;
        for(int i = 0; i < m; i++) {
            for(; j < edgeList.length && edgeList[j][2] < q[i][0]; j++) {
                uf.union(edgeList[j][0], edgeList[j][1]);
            }
            ans[q[i][1]] = uf.connected(queries[q[i][1]][0], queries[q[i][1]][1]);
        }
        return ans;
    }
}