[LeetCode 1462] Course Schedule IV

There are a total of n courses you have to take, labeled from 0 to n-1.

Some courses may have direct prerequisites, for example, to take course 0 you have first to take course 1, which is expressed as a pair: [1,0]

Given the total number of courses n, a list of direct prerequisite pairs and a list of queries pairs.

You should answer for each queries[i] whether the course queries[i][0] is a prerequisite of the course queries[i][1] or not.

Return a list of boolean, the answers to the given queries.

Please note that if course a is a prerequisite of course b and course b is a prerequisite of course c, then, course a is a prerequisite of course c.

 

Example 1:

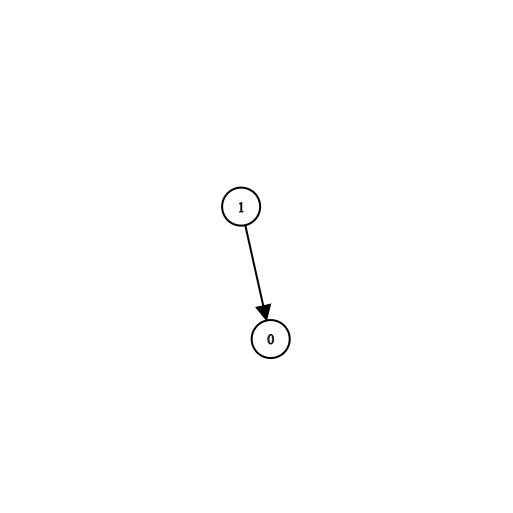
Input: n = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
Output: [false,true]
Explanation: course 0 is not a prerequisite of course 1 but the opposite is true.

Example 2:

Input: n = 2, prerequisites = [], queries = [[1,0],[0,1]]
Output: [false,false]
Explanation: There are no prerequisites and each course is independent.

Example 3:

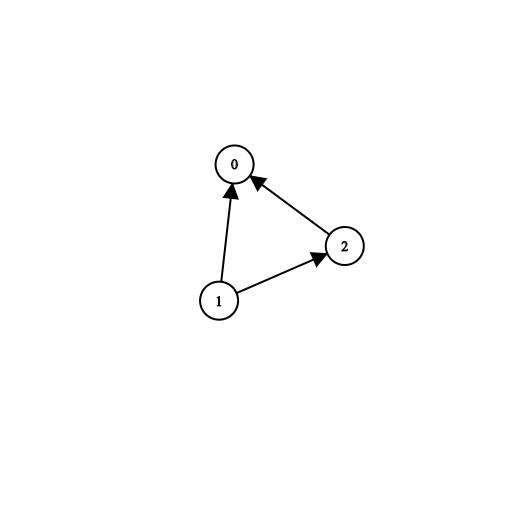
Input: n = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
Output: [true,true]

Example 4:

Input: n = 3, prerequisites = [[1,0],[2,0]], queries = [[0,1],[2,0]]
Output: [false,true]

Example 5:

Input: n = 5, prerequisites = [[0,1],[1,2],[2,3],[3,4]], queries = [[0,4],[4,0],[1,3],[3,0]]
Output: [true,false,true,false]

 

Constraints:

• 2 <= n <= 100
• 0 <= prerequisite.length <= (n * (n - 1) / 2)
• 0 <= prerequisite[i][0], prerequisite[i][1] < n
• prerequisite[i][0] != prerequisite[i][1]
• The prerequisites graph has no cycles.
• The prerequisites graph has no repeated edges.
• 1 <= queries.length <= 10^4
• queries[i][0] != queries[i][1]

 

This problem can be solved using multiple algorithms. 

For each prerequisite, let's denote it as U -> V, U is V's prerequisite. 

 

Solution 1. Topological sort variation

Topological sort provides one feasible course sequence to meet all prerequisites. We can modify the topological sort such that after V is visited, add V and all the courses that have V as their prerequisites to the set of courses that have U as their prerequisite. Building this mapping for one course will only take O(N^2) time and space, so it takes O(N^3) time and space to build the entire mapping. 

 

1. create a map, its keys are all possible courses, each value is a set of courses that have its corresponding key as prerequisite.

2. do a topological sort on the entire course graph, for each unvisited node U, do the following:

(a) if its child node V has not been visited, recursively perform topological sort on V. 

(b) then add V and its course collection in the mapping to U's mapping. This step must be done regardless if V is visited or not. Even if V has been visited, we still need to add V and its mapping collection to U's mapping, otherwise, U's mapping would not have these courses.

(c) mark U as visited after all its child nodes have been processed.

 

Doing the queries takes extra O(Number of queries) time.

 

 

class Solution {
    public List<Boolean> checkIfPrerequisite(int n, int[][] p, int[][] q) {
        List<Integer>[] g = new List[n];
        //pre: prerequisite course k -> courses that have course k as prerequisites
        Map<Integer, Set<Integer>> pre = new HashMap<>();
        boolean[] visited = new boolean[n];
        
        for(int i = 0; i < n; i++) {
            g[i] = new ArrayList<>();
            pre.put(i, new HashSet<>());
        }
        for(int[] pp : p) {
            g[pp[0]].add(pp[1]);
        }        
        for(int i = 0; i < n; i++) {
            topo(g, visited, pre, i);
        }
        List<Boolean> ans = new ArrayList<>();
        for(int[] qq : q) {
            ans.add(pre.get(qq[0]).contains(qq[1]));
        }
        return ans;
    }
    private void topo(List<Integer>[] g, boolean[] visited, Map<Integer, Set<Integer>> pre, int u) {
        if(!visited[u]) {       
            Set<Integer> prevSet = pre.get(u);
            for(int v : g[u]) {
                if(!visited[v]) {
                    topo(g, visited, pre, v);
                }  
                Set<Integer> set = pre.get(v);
                prevSet.add(v);
                prevSet.addAll(set);              
            }
            visited[u] = true;            
        }
    }
}

 

 

 

 

Solution 2. DFS 

Each query essentially asks if there is a path from queries[i][0] to queries[i][1]. Because N is relatively small(only up to 100), we can perform a simple dfs for each query, the runtime is O(100 * 10^4) -- O(10^6). 

 

The key point here is that in dfs, we need to track if a node has been visited or not to avoid redundant work. Think of a case where U has 2 children V1 and V2, V1 and V2 share the same child node of X, X has not path leading to the target node. From U, we dfs on V1, then dfs on X. This will return false. Then we need to dfs on V2, if we do not know that X has already been explored without success, we would explore it again. This will lead to TLE.

 

 

class Solution {
    public List<Boolean> checkIfPrerequisite(int n, int[][] p, int[][] q) {
        List<Integer>[] g = new List[n];
        for(int i = 0; i < n; i++) {
            g[i] = new ArrayList<>();
        }
        for(int[] pp : p) {
            g[pp[0]].add(pp[1]);
        }
        List<Boolean> ans = new ArrayList<>();
        for(int[] qq : q) {
            ans.add(reach(g, qq[0], qq[1], new boolean[n]));
        }
        return ans;
    }
    
    private boolean reach(List<Integer>[] g, int src, int dst, boolean[] visited) {
        if(src == dst) {
            return true;
        }
        for(int next : g[src]) {          
            if(!visited[next] && reach(g, next, dst, visited)) {
                return true;
            }
        }
        visited[src] = true;
        return false;
    }
}

 

 

Solution 3. BFS + Transitive Closure

Alternatively, we can create a 2D grid that stores all course pairs' relations. For each course node, start a bfs from it, any reachable nodes have this starting course as its prerequisite.

 

Similar with the DFS approach, we need to track if a path has been explored. We can use the 2D transitive closure to do this. For a given node X, if grid[start][X] has been set to true, we know that there is a shorter path from start to X and X has been added to queue once. 

 

class Solution {
    public List<Boolean> checkIfPrerequisite(int n, int[][] p, int[][] q) {
        boolean[][] grid = new boolean[n][n];
        List<Integer>[] g = new List[n];
     
        for(int i = 0; i < n; i++) {
            g[i] = new ArrayList<>();
        }
        for(int[] pp : p) {
            g[pp[0]].add(pp[1]);
        } 
        for(int i = 0; i < n; i++) {
            bfs(g, grid, i);
        }
        List<Boolean> ans = new ArrayList<>();
        for(int[] qq : q) {
            ans.add(grid[qq[0]][qq[1]]);
        }
        return ans;
    }
    private void bfs(List<Integer>[] g, boolean[][] grid, int start) {
        Queue<Integer> q = new LinkedList<>();
        q.add(start);
        
        while(q.size() > 0) {
            int curr = q.poll();
            if(!grid[start][curr]) {
                grid[start][curr] = true;
                for(int next : g[curr]) {
                    q.add(next);
                }
            }
        }
    }
}

 

 

Solution 4.  Floyd-Warshall Algorithm variation for transitive closure

 

Dynamic programming Floyd-Warshall: let k be the permitted intermediate nodes [0, k] for a given pair(i, j). Add one more allowed intermediate node at the most outer loop to control the size of the current subproblems.

 

dp[i][j]: if there is a path from i to j.  dp[i][j] = dp[i][j] || dp[i][k] && dp[k][j]. 

 

class Solution {
    public List<Boolean> checkIfPrerequisite(int n, int[][] p, int[][] q) {
        boolean[][] dp = new boolean[n][n];
        for(int i = 0; i < n; i++) {
            dp[i][i] = true;
        }
        for(int[] pp : p) {
            dp[pp[0]][pp[1]] = true;
        } 
        
        for(int k = 0; k < n; k++) {
            for(int i = 0; i < n; i++) {
                for(int j = 0; j < n; j++) {
                    if(dp[i][j]) {
                        continue;
                    }
                    dp[i][j] |= (dp[i][k] && dp[k][j]);
                }
            }
        }
        List<Boolean> ans = new ArrayList<>();
        for(int[] qq : q) {
            ans.add(dp[qq[0]][qq[1]]);
        }
        return ans;
    }
}