最小二乘法求线性回归的python实现
原文:
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
本文链接:https://blog.csdn.net/qq_38003892/article/details/84495172
1 核心思想
通过最小化方差,使得拟合结果无限接近目标结果。
2 通过一元线性方程举例说明

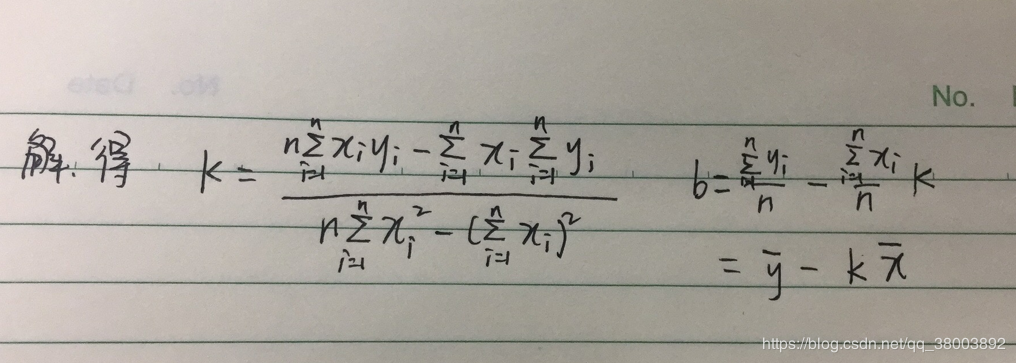
3 通过python实现一元线性拟合
import matplotlib.pyplot as plt
import random
# 用于存储x,y拟合数据
x = []
y = []
# 数据个数
n = 10
# 随机生成x,y
for i in range(n):
x.append(random.randint(0, 9))
y.append(random.randint(0, 9))
print(x, y)
# 根据推到出来的公式计算k,b
sum_xy = 0
sum_x = 0
sum_y = 0
sum_xx = 0
for i in range(n):
sum_xy += x[i] * y[i]
sum_x += x[i]
sum_y += y[i]
sum_xx += x[i] ** 2
print(sum_xy, sum_x, sum_y, sum_xx)
k = (n * sum_xy - sum_x * sum_y) / (n * sum_xx - sum_x ** 2)
b = sum_y / n - k * sum_x / n
print(k, b)
# 根据x计算拟合的y值
new_y = []
for i in range(n):
new_y.append(k * x[i] + b)
# 画出原始数据点以及拟合好的直线
plt.title("Least squares")
plt.xlim(right=10, left=0)
plt.ylim(top=10, bottom=0)
plt.xlabel("x")
plt.ylabel("y")
plt.plot(x, new_y, color='black')
plt.scatter(x, y, color='red')
plt.show()
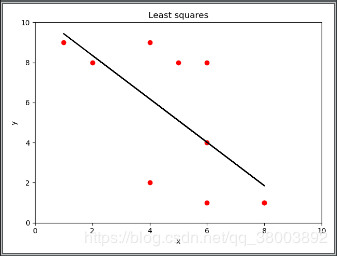
运行结果(因为数据时随机生成的每次代码运行结果都会不同)