noip2012 P1081 开车旅行

小 A 和小 B 决定利用假期外出旅行，他们将想去的城市从 1 到 N 编号，且编号较小的城市在编号较大的城市的西边，已知各个城市的海拔高度互不相同，记城市 i 的海拔高度为Hi，城市 i 和城市 j 之间的距离 d[i,j]恰好是这两个城市海拔高度之差的绝对值，即d[i,j] = |Hi− Hj|。旅行过程中，小 A 和小 B 轮流开车，第一天小 A 开车，之后每天轮换一次。他们计划选择一个城市 S 作为起点，一直向东行驶，并且最多行驶 X 公里就结束旅行。小 A 和小 B的驾驶风格不同，小 B 总是沿着前进方向选择一个最近的城市作为目的地，而小 A 总是沿着前进方向选择第二近的城市作为目的地（注意：本题中如果当前城市到两个城市的距离相同，则认为离海拔低的那个城市更近）。如果其中任何一人无法按照自己的原则选择目的城市，或者到达目的地会使行驶的总距离超出 X 公里，他们就会结束旅行。

在启程之前，小 A 想知道两个问题：

对于一个给定的 X=X0，从哪一个城市出发，小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值最小（如果小 B 的行驶路程为 0，此时的比值可视为无穷大，且两个无穷大视为相等）。如果从多个城市出发，小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值都最小，则输出海拔最高的那个城市。
对任意给定的 X=Xi和出发城市 Si，小 A 开车行驶的路程总数以及小 B 行驶的路程

总数。

【数据范围】

对于30%的数据，有 1≤N≤20 ， 1≤M≤20 ；

对于40%的数据，有 1≤N≤100 ，1≤M≤100 ；

对于50%的数据，有 1≤N≤100 ，1≤M≤1000 ；

对于70%的数据，有 1≤N≤1000 ，1≤M≤10000 ；

对于100%的数据，有 1≤N≤100000 ， 1≤M≤10000 ， -1000000000≤Hi≤1000000000，0≤X0≤1000000000 ， 1≤Si≤N，

0≤Xi≤1000000000 ，数据保证 $H_iHi 互不相同。$

输入输出格式

输入格式：

第一行包含一个整数 N，表示城市的数目。

第二行有 N 个整数，每两个整数之间用一个空格隔开，依次表示城市 1 到城市 N 的海拔高度，即 H1，H2，……，Hn，且每个 Hi都是不同的。

第三行包含一个整数 X0。

第四行为一个整数 M，表示给定 M 组 Si和 Xi。

接下来的 M 行，每行包含 2 个整数 Si和 Xi，表示从城市 Si出发，最多行驶 Xi公里。

输出格式：

输出共 M+1 行。

第一行包含一个整数 S0，表示对于给定的 X0，从编号为 S0的城市出发，小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值最小。

接下来的 M 行，每行包含 2 个整数，之间用一个空格隔开，依次表示在给定的 Si和

Xi下小 A 行驶的里程总数和小 B 行驶的里程总数。

输入输出样例

输入样例#1：复制

输出样例#1：复制

输入样例#2：复制

10 
4 5 6 1 2 3 7 8 9 10 
7 
10 
1 7 
2 7 
3 7 
4 7 
5 7 
6 7 
7 7 
8 7 
9 7 
10 7

输出样例#2：复制

说明

【输入输出样例 1 说明】

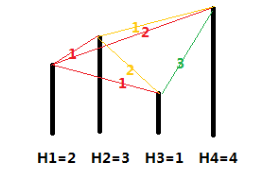
各个城市的海拔高度以及两个城市间的距离如上图所示。

如果从城市 1 出发，可以到达的城市为 2,3,4，这几个城市与城市 1 的距离分别为 1,1,2，但是由于城市 3 的海拔高度低于城市 2，所以我们认为城市 3 离城市 1 最近，城市 2 离城市

1 第二近，所以小 A 会走到城市 2。到达城市 2 后，前面可以到达的城市为 3,4，这两个城市与城市 2 的距离分别为 2,1，所以城市 4 离城市 2 最近，因此小 B 会走到城市 4。到达城市 4 后，前面已没有可到达的城市，所以旅行结束。

如果从城市 2 出发，可以到达的城市为 3,4，这两个城市与城市 2 的距离分别为 2,1，由于城市 3 离城市 2 第二近，所以小 A 会走到城市 3。到达城市 3 后，前面尚未旅行的城市为

4，所以城市 4 离城市 3 最近，但是如果要到达城市 4，则总路程为 2+3=5>3，所以小 B 会直接在城市 3 结束旅行。

如果从城市 3 出发，可以到达的城市为 4，由于没有离城市 3 第二近的城市，因此旅行

还未开始就结束了。

如果从城市 4 出发，没有可以到达的城市，因此旅行还未开始就结束了。

【输入输出样例 2 说明】

当 X=7 时，如果从城市 1 出发，则路线为 1 -> 2 -> 3 -> 8 -> 9，小 A 走的距离为 1+2=3，小 B 走的距离为 1+1=2。（在城市 1 时，距离小 A 最近的城市是 2 和 6，但是城市 2 的海拔更高，视为与城市 1 第二近的城市，所以小 A 最终选择城市 2；走到 9 后，小 A 只有城市 10 可以走，没有第 2 选择可以选，所以没法做出选择，结束旅行）

如果从城市 2 出发，则路线为 2 -> 6 -> 7 ，小 A 和小 B 走的距离分别为 2，4。

如果从城市 3 出发，则路线为 3 -> 8 -> 9，小 A 和小 B 走的距离分别为 2，1。

如果从城市 4 出发，则路线为 4 -> 6 -> 7，小 A 和小 B 走的距离分别为 2，4。

如果从城市 5 出发，则路线为 5 -> 7 -> 8 ，小 A 和小 B 走的距离分别为 5，1。

如果从城市 6 出发，则路线为 6 -> 8 -> 9，小 A 和小 B 走的距离分别为 5，1。

如果从城市 7 出发，则路线为 7 -> 9 -> 10，小 A 和小 B 走的距离分别为 2，1。

如果从城市 8 出发，则路线为 8 -> 10，小 A 和小 B 走的距离分别为 2，0。

如果从城市 9 出发，则路线为 9，小 A 和小 B 走的距离分别为 0，0（旅行一开始就结

束了）。

如果从城市10出发，则路线为 10，小A 和小B 走的距离分别为0，0。

从城市 2 或者城市 4 出发小 A 行驶的路程总数与小 B 行驶的路程总数的比值…

———————————————————————————————

这道题算法很明显倍增QAQ 但是处理起来会比较麻烦qwq

首先我们可以先预处理出每个点在编号比他大的点中的最近点和次进点

这个利用STL的set很好实现

然后我们就可以来倍增辣 f[i][j]表示i这个点往后跳2^j步要跳到哪

A[i][j] B[i][j] 表示i这个点往后跳2^j步A/B 需要走的路程然后就可以写辣23333

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<set>
#include<cmath>
#define LL long long
using std::sort;
const int M=2e5+7;
const LL inf=0x3f3f3f3f3f3f3f3f;
LL read(){
    LL ans=0,f=1,c=getchar();
    while(c<'0'||c>'9'){if(c=='-') f=-1; c=getchar();};
    while(c>='0'&&c<='9'){ans=ans*10+(c-'0'); c=getchar();}
    return ans*f;
}
LL n,m,h[M],d1[M][2],d2[M][2];
struct pos{
    LL id,h;
    bool operator <(const pos &x)const{return h<x.h;}
};
std::multiset<pos>tr;
typedef std::multiset<pos>::iterator IT;
void calc(int i,IT it){
    LL now=abs(it->h-h[i]);
    if(now<d1[i][0]||(now==d1[i][0]&&h[it->id]<h[d1[i][1]])){
        d2[i][0]=d1[i][0]; d2[i][1]=d1[i][1];
        d1[i][0]=now;        d1[i][1]=it->id;    
    }
    else if(now<d2[i][0]||(now==d2[i][0]&&h[it->id]<h[d2[i][1]])) d2[i][0]=now,d2[i][1]=it->id;
}
LL f[M][22],A[M][22],B[M][22],X;
LL ansh;
double mx=inf;
int main(){
    n=read();
    for(int i=1;i<=n;i++) h[i]=read();
    memset(d1,0x3f,sizeof(d1));
    memset(d2,0x3f,sizeof(d2));
    tr.insert((pos){n,h[n]});
    for(int i=n-1;i;i--){
        IT it=tr.lower_bound((pos){0,h[i]});
        if(it!=tr.end()){
            calc(i,it);
            it++; if(it!=tr.end()) calc(i,it); it--;
        }
        if(it!=tr.begin()){
            it--; calc(i,it);
            if(it!=tr.begin()) it--,calc(i,it);    
        }
        tr.insert((pos){i,h[i]});
    }
    memset(f,0x3f,sizeof(f));memset(A,0x3f,sizeof(A));memset(B,0x3f,sizeof(B));
    for(int i=1;i<=n;i++)if(d2[i][1]<=n&&d1[d2[i][1]][1]<=n){
        f[i][0]=d1[d2[i][1]][1];
        A[i][0]=d2[i][0];
        B[i][0]=d1[d2[i][1]][0];    
    }
    for(int j=1;j<=20;j++)
    for(int i=1;i<=n;i++)if(f[i][j-1]<=n&&f[f[i][j-1]][j-1]<=n){
        f[i][j]=f[f[i][j-1]][j-1];
        A[i][j]=A[i][j-1]+A[f[i][j-1]][j-1];
        B[i][j]=B[i][j-1]+B[f[i][j-1]][j-1];
    }
    X=read();
    for(int i=1;i<=n;i++){
        int ly=i;
        LL Ca=0,Cb=0;
        for(int j=20;j>=0;j--)if(f[ly][j]<=n&&Ca+A[ly][j]+Cb+B[ly][j]<=X){
            Ca+=A[ly][j]; 
            Cb+=B[ly][j];
            ly=f[ly][j];
        }
        if(d2[ly][1]<=n&&Ca+Cb+d2[ly][0]<=X) Ca+=d2[ly][0];
        double now;
        if(!Cb) now=0.5*inf;
        else now=1.0*Ca/(1.0*Cb);
        if(now<mx){mx=now; ansh=i;}
        else if(now==mx&&h[i]>h[ansh]) ansh=i;
    }printf("%lld\n",ansh);
    LL s; 
    m=read();
    for(int i=1;i<=m;i++){
        s=read(); X=read();
        int ly=s;
        LL Ca=0,Cb=0;
        for(int j=20;j>=0;j--)if(f[ly][j]<=n&&Ca+A[ly][j]+Cb+B[ly][j]<=X){
            Ca+=A[ly][j]; 
            Cb+=B[ly][j];
            ly=f[ly][j];
        }
        if(d2[ly][1]<=n&&Ca+Cb+d2[ly][0]<=X) Ca+=d2[ly][0];
        printf("%lld %lld\n",Ca,Cb);
    }
    return 0;
}

View Code

posted @ 2017-11-02 21:06 友人Aqwq 阅读(172) 评论(0) 编辑收藏举报

刷新页面返回顶部

友人A

——QAQ

noip2012 P1081 开车旅行

输入输出格式

输入输出样例

说明

公告