51nod 1079 中国剩余定理

一个正整数K，给出K Mod 一些质数的结果，求符合条件的最小的K。例如，K % 2 = 1, K % 3 = 2, K % 5 = 3。符合条件的最小的K = 23。

 

Input

第1行：1个数N表示后面输入的质数及模的数量。（2 <= N <= 10)
第2 - N + 1行，每行2个数P和M，中间用空格分隔，P是质数，M是K % P的结果。（2 <= P <= 100, 0 <= K < P)

Output

输出符合条件的最小的K。数据中所有K均小于10^9。

Input示例

3
2 1
3 2
5 3

Output示例

23
———————————————————————————
这道题是裸的剩余定理

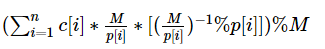
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
LL read(){
    LL ans=0,f=1,c=getchar();
    while(c<'0'||c>'9'){if(c=='-') f=-1; c=getchar();}
    while(c>='0'&&c<='9'){ans=ans*10+(c-'0'); c=getchar();}
    return ans*f;
}
int n;
LL ans,c[15],p[15],mod;
LL inv(LL a,LL b,LL c){
    LL ans=1;
    while(b){
        if(b&1) ans=ans*a%c;
        b>>=1; a=a*a%c;
    }return ans;
}
int main(){
    n=read(); mod=1;
    for(int i=1;i<=n;i++){
        p[i]=read(); c[i]=read();
        mod*=p[i];
    }
    for(int i=1;i<=n;i++){
        LL ly=mod/p[i]*c[i]%mod;
        ans=(ans+(__int128)ly*inv(mod/p[i],p[i]-2,p[i]))%mod;
    }printf("%lld\n",ans);
    return 0;
}