AtCoder Regular Contest 082 E

Problem Statement

You are given N points (x_i,y_i) located on a two-dimensional plane. Consider a subset S of the N points that forms a convex polygon. Here, we say a set of points S forms a convex polygon when there exists a convex polygon with a positive area that has the same set of vertices as S. All the interior angles of the polygon must be strictly less than 180°.

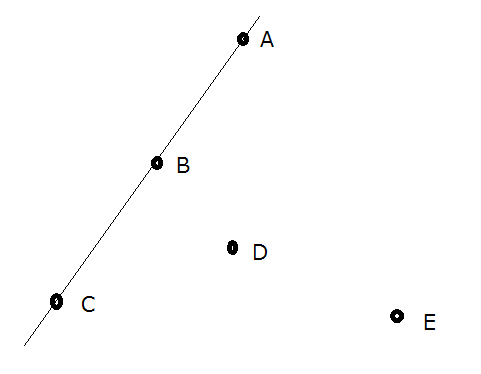
For example, in the figure above, {A,C,E} and {B,D,E} form convex polygons; {A,C,D,E}, {A,B,C,E}, {A,B,C}, {D,E} and {} do not.

For a given set S, let n be the number of the points among the N points that are inside the convex hull of S (including the boundary and vertices). Then, we will define the score of S as 2^n−|S|.

Compute the scores of all possible sets S that form convex polygons, and find the sum of all those scores.

However, since the sum can be extremely large, print the sum modulo 998244353.

Constraints

• 1≤N≤200
• 0≤x_i,y_i<10⁴(1≤i≤N)
• If i≠j, x_i≠x_j or y_i≠y_j.
• x_i and y_i are integers.

---

Input

The input is given from Standard Input in the following format:

N
x1 y1
x2 y2
:
xN yN

Output

Print the sum of all the scores modulo 998244353.

---

Sample Input 1

Copy

4
0 0
0 1
1 0
1 1

Sample Output 1

Copy

5

We have five possible sets as S, four sets that form triangles and one set that forms a square. Each of them has a score of 2⁰=1, so the answer is 5.

---

Sample Input 2

Copy

5
0 0
0 1
0 2
0 3
1 1

Sample Output 2

Copy

11

We have three "triangles" with a score of 1 each, two "triangles" with a score of 2 each, and one "triangle" with a score of 4. Thus, the answer is 11.

---

Sample Input 3

Copy

1
3141 2718

Sample Output 3

Copy

0

There are no possible set as S, so the answer is 0.

————————————————————————————————

题意就是求对每个凸多边形，求(2^内部点数)的和 这里我们可以进行一波转换
考虑每个凸多边形，其内部的点每个都可以选择删与不删，得到的方案数就是贡献
而这个转化恰好就等价于不共线的子集数 共线就是子集内所有点在同一直线上
这样之后我们只要用总的子集数减去共线的子集数就好了
枚举直线倾斜角，算包含至少两点的共线子集有几个
倾斜角用枚举两两点得到 然后求gcd使得每个倾角有唯一表达形式
将向量(x,y)转为唯一表示法，然后求个hash
方便sort比较 然后并查集维护 这样复杂度是n^3
当然也可以把斜率离散化从sort换成散列表或者基数排序 然后并查集换成连边，忽略没连到边的点就n^2了

#include<cstdio>
#include<cstring>
#include<algorithm>
const int M=207,mod=998244353;
int read(){
    int ans=0,f=1,c=getchar();
    while(c<'0'||c>'9'){if(c=='-') f=-1; c=getchar();}
    while(c>='0'&&c<='9'){ans=ans*10+(c-'0'); c=getchar();}
    return ans*f; 
}
int n,f[M],sz[M];
int find(int x){while(f[x]!=x) x=f[x]=f[f[x]]; return x;}
int gcd(int x,int y){return y?gcd(y,x%y):x;} 
struct pos{int x,y;}q[M];
int cnt;
struct node{
    int u,v,w;
    bool operator <(const node &x)const{return w<x.w;}
    void calc(){
        int p=find(u),q=find(v);
        if(p!=q) f[q]=p,sz[p]+=sz[q];
    }
}e[M*M];
int pw[M],ans;
void prepare(){
    pw[0]=1; 
    for(int i=1;i<=n;i++) pw[i]=(pw[i-1]<<1)%mod;
}
int main(){
    n=read(); 
    prepare(); ans=(pw[n]-n-1)%mod;
    for(int i=1;i<=n;i++) q[i].x=read(),q[i].y=read();
    for(int i=1;i<=n;i++)
        for(int j=1;j<i;j++){
            int x=q[i].x-q[j].x,y=q[i].y-q[j].y,g=gcd(x,y);
            x/=g; y/=g;
            if(!x) y=1;
            if(!y) x=1;
            if(x<0) x=-x,y=-y;
            e[++cnt]=(node){i,j,x*30000+y};
        }
    std::sort(e+1,e+1+cnt);
    for(int i=1,j=1;i<=cnt;i=j){
        for(int k=1;k<=n;k++) sz[f[k]=k]=1;
        while(j<=cnt&&e[j].w==e[i].w) e[j++].calc();
        for(int k=1;k<=n;k++) if(f[k]==k&&sz[k]>=2) ans=(ans-pw[sz[k]]+sz[k]+1)%mod;
    }printf("%d\n",(ans+mod)%mod);
    return 0;
}