汕头市队赛 SRM 06 C 秀恩爱

C 秀恩爱 SRM 06

背景&&描述

        KPM坐在直升机上俯瞰小渔村景象。

        渔村可看作二维平面，密密麻麻地到处都是单身狗，KPM当前所在坐标为(sx,sy)。

        KPM的后宫团们自发地聚集在一起为他送行，从空中看，后宫团形成了一个多边形。

        当然了KPM是不在那个多边形内的。

        直升机突然开始原地转圈，后宫团们因为想看着KPM的正脸，所以也跟着以KPM所在坐标为中心旋转。

        后宫团所经之处单身狗尸横遍野。赶来救治伤员的医护人员想知道，多边形扫过的面积是多少。

        

        注意，本题不保证横坐标互不相同、纵坐标互不相同什么的。

        请注意运算过程中可能出现的/0等问题。

输入格式

        第一行三个整数，n,sx,sy。n表示多边形的顶点数。

        接下来n行每行俩整数，分别表示多边形一个顶点的横纵坐标。

        （顶点是按照顺时针或者逆时针顺序给出的，并且所有点的坐标绝对值<=，保证不存在共线的三个顶点）

输出格式

一个整数，表示面积四舍五入为整数的结果。

样例输入

3 0 0
0 1
-1 2
1 2

样例输出

13

数据范围与约定

• 对于100%的数据:

样例解释

 

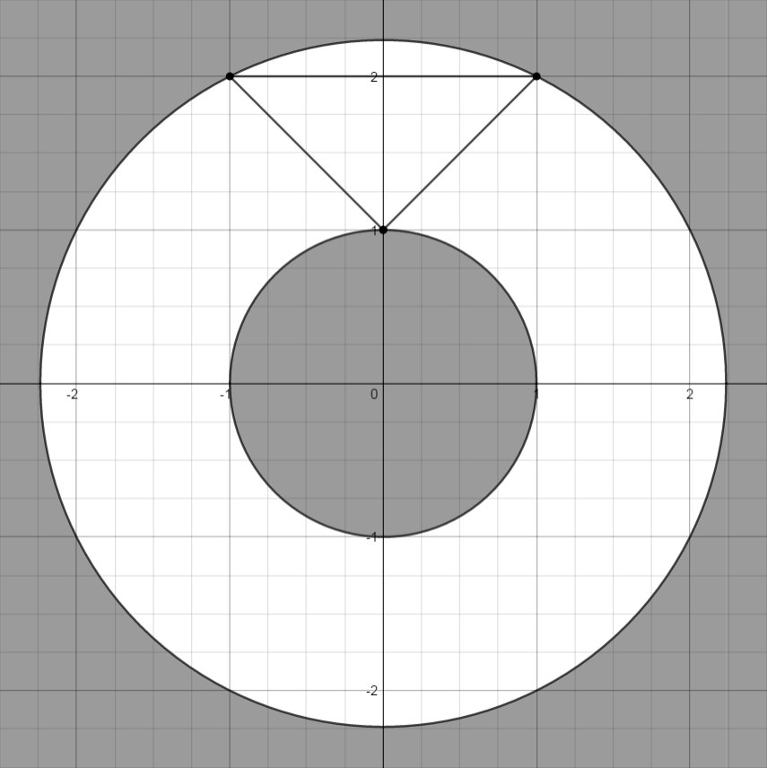
这道题主要是求最小半径以及最大半径

易证明最大半径mx一定在顶点位置

而最小半径也可能在两点的直线上

明白这一点后代码就很好实现了 不过要注意精度问题 今天似乎大爷们都被精度卡了 2333

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
using namespace std;
const int M=155;
const double P=3.141592653589793238462643383279502884;
LL read(){
    LL ans=0,f=1,c=getchar();
    while(c<'0'||c>'9'){if(c=='-') f=-1; c=getchar();}
    while(c>='0'&&c<='9'){ans=ans*10+(c-'0'); c=getchar();}
    return ans*f;
}
double mx,mn=1e15;
double k1,k2,b,L,mxx,mnx,nx;
LL x[M],y[M],n,sx,sy;
int main()
{
    n=read(); sx=read(); sy=read();
    for(int i=1;i<=n;i++){
        x[i]=read()-sx; y[i]=read()-sy;
        L=1.0*(fabs(x[i])*fabs(x[i])+fabs(y[i])*fabs(y[i]));
        mx=max(mx,L);
        mn=min(mn,L);
    }
    for(int i=1;i<=n;i++){
        int j=i+1<=n?i+1:1;
        if(x[i]==x[j]){
            if((y[i]>0&&y[j]<0)||(y[i]<0&&y[j]>0)) mn=min(mn,(double)x[i]*x[j]);
            continue;
        }
        mxx=max(x[i],x[j]);
        mnx=min(x[i],x[j]);
        if(y[i]==y[j]){
            if(mxx>0&&mnx<0) mn=min(mn,(double)y[i]*y[j]);
            continue;
        }
        k1=(double)(y[i]-y[j])/(x[i]-x[j]);
        b=(double) y[i]-k1*x[i];
        k2=-1.0/k1;
        nx=b/(k2-k1);
        if(nx>mxx||nx<mnx) continue;
        L=b/sqrt(k1*k1+1);
        mn=min(mn,L*L);
    }
    printf("%lld",(long long)(P*(mx-mn)+0.5));
    return 0;
}