《数据结构与面向对象程序设计》第10周学习总结
学号20182329 2019-2020-1 《数据结构与面向对象程序设计》第10周学习总结
教材学习内容总结
- 实现二叉排序树,并学会编写删除、添加、插入,还有二叉排序树的遍历
- 学习图的有关知识,了解有向图和无向图的区别,
- 学习带权图,学会计算带权图的算法,最佳的算法。
- 学习图的各种遍历,比如深度优先遍历和广度优先遍历。
- 学习生成最小树的方法
- 学会生成图的邻接矩阵的方法,还有计算每个节点的出度入度方法实现
- 学会每个图的计算度的方法,还有不通过遍历进行的。
教材学习中的问题和解决过程啊
- 问题1:在学习计算带权图的各个路径上的带权值值之和时,发现自己用中序遍历的方法将带权图的总值计算出来,但是在计算各个节点上的带全值时,有些节点总是少一个全职。
- 问题1解决方法:后来认识到图不一定是完全二叉树,所以在进行这个遍历时会少掉一些全职或者说是子叶,然后我用学习了深度优先遍历的代码,虽然算法比较慢,但是可以不遗漏,一下是深度优先遍历的代码:
public void dFS_AM(int site) { //输入深度优先遍历的开始顶点
System.out.println(this.vexs[site]); //输出该顶点
this.visited[site] = true; //置访问标志为true
for(int i = 0; i < this.vexs.length; i++) { //依次查找未访问邻接点,并以该邻接点为始点调用深度优先遍历算法
if(this.arcs[site][i] != 0 && !this.visited[i]) {
this.dFS_AM(i);
}
}
}
- 问题2::一开始我使用的是在类里面编写循环代码,来进行查找用while语句实现并判断,但是后来我发现自己的循环会一直走到链的最后一位,然后再弹出,根本不是我需要的查找数字。
- 问题2解决方案:后来发现我的条件语句有很多问题,一一改正后,自己有重写了一个递归调用的方法,比之前的循环方法减少了很多代码量。
- 问题3:在我编写广度优先遍历的方法时,应为在课上听来是有递归算法和不递归算法两种情况,后来我先做的非递归算法,在同学的帮助下还有老师的上课的讲解,很轻松的做了出来,但是在做递归算法时,发现自己总是会遍历不到最下面的一层子夜。
- 问题3解决方法:条件方法设置错误,和遍历的方法不匹配,
这是代码:
public void bFSTraverse() {
this.visited = new boolean[this.vexs.length]; //初始化访问标志数组
for(int i = 0; i < this.visited.length; i++) {
this.visited[i] = false;
}
for(int i = 0; i < this.visited.length; i++) {
if(!this.visited[i]) { //对未访问的顶点调用广度优先遍历算法
bFS_AM(i);
}
}
}
代码调试中的问题和解决过程
-
问题1:在进行测试代码时,我先将他们的邻接矩阵列出来,在根据邻接矩阵来进行测试代码是否真确
-
问题1解决方法:这个方法无论怎样测试都是正确的,用结果测试结果本来就是不正确的
-
问题2:在编写测试代码的时候我吧文件读入,然后按照字符输出发现只是输出了路径的地址。
-
解决方法:我是直接把自己以前编写的读取字符型和数字的读取方法直接搬了过来,没有改正返回值,而且也没有用read写入。
代码托管
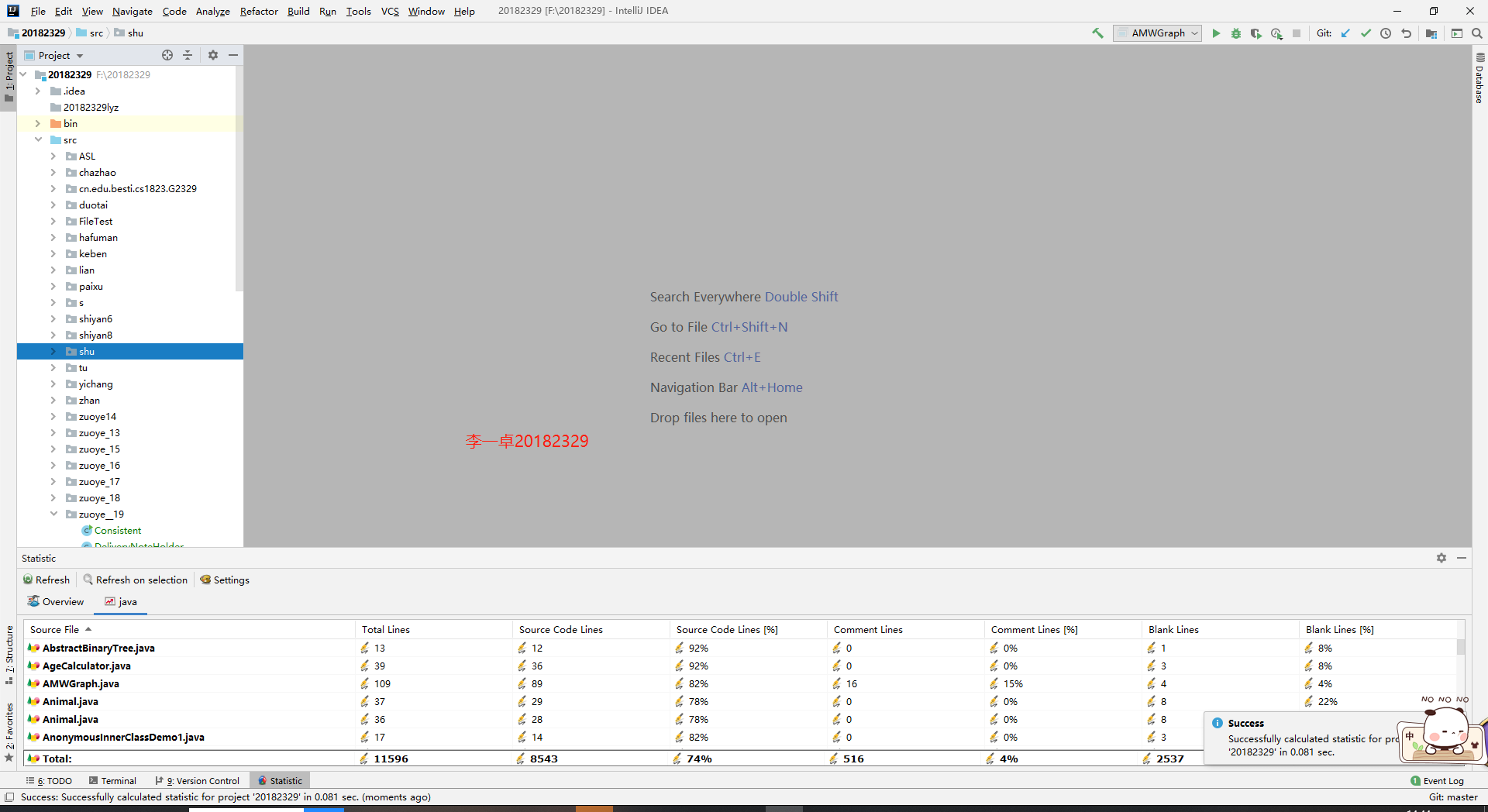
(statistics.sh脚本的运行结果截图)
上周考试错题总结
错题
结对及互评
评分标准
点评模板:
-
博客中值得学习的或问题:
- 本博客体现许多java连接的问题,发现了一些排序和查找的优点。
- 但是博客在课本自学方面存在一点问题,并没有将所有知识点列出,只是课本编程实列的学习问题的解决。
- 这篇博客的代码问题并没有将各种排序的方法事列出来,也没有将查找的算法列出来。
-
代码中值得学习的或问题:
- 本博客在提出代码编写错吴时,虽然解析比较完整,没有展示出比较全面的图片。
- 本博客存在设置类(抽象类)时的错误,希望改正。
-
基于评分标准,我给本博客打分:10分。得分情况如下:
-
正确排版要素齐全(+1)
-
使用makedown格式(+1)
-
教材问题(+3)
-
代码调试问题(+3)
-
错题深入(+1)
-
点评认真(+1)
点评过的同学博客和代码
- 本周结对学习情况
其他(感悟、思考等,可选)
学习图的实现,我发现每一个具体的图,就是该类的一个实例化对象,因此我们可以在构造函数中实现图的创建。创建好图后,我们还要实现图的遍历。由于图已经被我们抽象成一个类,因此我们可以将图的遍历定义成类的方法。对于连通图,调用遍历算法后即可访问所有结点,但对于非连通图,调用遍历算法后仍有一些结点没有被访问,需要从图中另选一个未被访问的顶点再次调用遍历算法。因此需要附设一个访问标志数组visited[n],来记录被访问的结点。
图的实现代码如下:
public AMGraph(int vexNum,int arcNum) { //输入点的个数和边的个数
this.vexs = new String[vexNum];
this.arcs = new int[vexNum][vexNum];
System.out.print("请依次输入顶点值,以空格隔开:");
Scanner sc = new Scanner(System.in);
for(int i = 0; i < vexNum; i++) { //根据输入建立点集
this.vexs[i] = sc.next();
}
for(int i = 0; i < vexNum; i++) { //初始化边集
for(int j = 0; j < vexNum; j++) {
this.arcs[i][j] = 0; //0表示该位置所对应的两顶点之间没有边
}
}
start:for(int i = 0; i < arcNum; i++) { //开始建立边集
sc = new Scanner(System.in);
int vex1Site = 0;
int vex2Site = 0;
String vex1 = null;
String vex2 = null;
System.out.print("请输入第" + (i+1) + "条边所依附的两个顶点,以空格隔开:");
vex1 = sc.next();
vex2 = sc.next();
for(int j = 0; j < this.vexs.length; j++) { //查找输入的第一个顶点的位置
if (this.vexs[j].equals(vex1)) {
vex1Site = j;
break;
}
if (j == this.vexs.length - 1) {
System.out.println("未找到第一个顶点,请重新输入!");
i--;
continue start;
}
}
for (int j = 0; j < this.vexs.length; j++) { //查找输入的第二个顶点的位置
if(this.vexs[j].equals(vex2)) {
vex2Site = j;
break;
}
if (j == this.vexs.length - 1) {
System.out.println("未找到第二个顶点,请重新输入!");
i--;
continue start;
}
}
if(this.arcs[vex1Site][vex2Site] != 0) { //检测该边是否已经输入
System.out.println("该边已存在!");
i--;
continue start;
}else {
this.arcs[vex1Site][vex2Site] = 1; //1表示该位置所对应的两顶点之间有边
this.arcs[vex2Site][vex1Site] = 1; //对称边也置1
}
}
System.out.println("基于邻接矩阵的无向图创建成功!");
sc.close();
}
参考资料
Java程序设计
Android程序设计
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 6000行 | 30篇 | 400小时 | |
| 第一周 | 107/107 | 2/2 | 15/15 | |
| 第二周 | 454/526 | 2/4 | 32/47 | |
| 第三周 | 988/1514 | 2/6 | 31/78 | |
| 第五周 | 757/2271 | 2/8 | 31/109 | |
| 第六周 | 875/3146 | 1/9 | 31/140 | |
| 第七周 | 1282/4428 | 2/11 | 58/198 | |
| 第八周 | 1972/6400 | 2/13 | 36/234 | |
| 第九周 | 3799/10199 | 3/13 | 55/289 | |
| 第十周 | 1397/11596 | 2/13 | 28/317 | |
| 尝试一下记录「计划学习时间」和「实际学习时间」,到期末看看能不能改进自己的计划能力。这个工作学习中很重要,也很有用。 | ||||
| 耗时估计的公式:Y=X+X/N ,Y=X-X/N,训练次数多了,X、Y就接近了。 |
-
计划学习时间:60小时
-
实际学习时间:58小时
-
改进情况:树好难啊。



