复数及三角函数学习笔记

复数与三角函数是学习OI数学中比较基础的内容，对于初中选手不是很友好。

定义

复数

定义一个常数 $i=\sqrt{1}$，那么所有形如 $a+bi$ 的数都是复数。（$a,b\in \R$）

一般用 $z$ 表示复数。

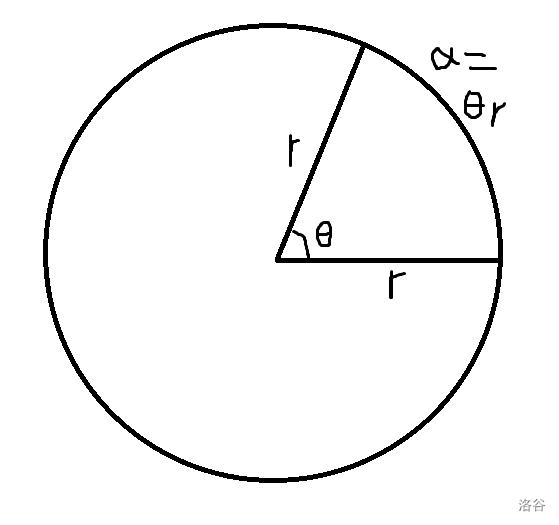
弧度制与角度制互转

$\pi\ rad=180^\circ$，$rad$ 可以省略。

这两者都是用于表示在圆中的占比。角度制表示的是对应角在整个圆的角（$360^\circ$），弧度制表示的是对应弧与半径的比例。两个的关系就像小数与分数一样。

复平面

一般我们考虑复数的几何意义，都在复平面上考虑。

复平面长成下面这个样子：

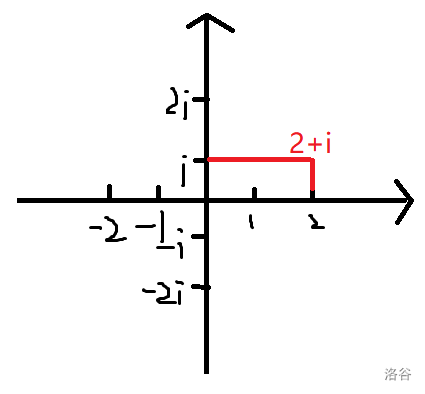
在这个坐标系上点 $(a,b)$ 所代表的值为 $a+bi$。

不难发现在这个坐标系上一个点只能代表一个复数，一个复数恰好对应一个点。

向量

向量是同时具有方向和大小的量，在几何中用带箭头的线段表示，这个线段的长度及其箭头所指方向与其表示的内容相关。

幅角

以实轴正方向为始边，$z$ 所对应的向量 $Z$ 为终边的角 $\theta$ 称为复数 $z$ 的幅角。

大概就像下图这个样子：

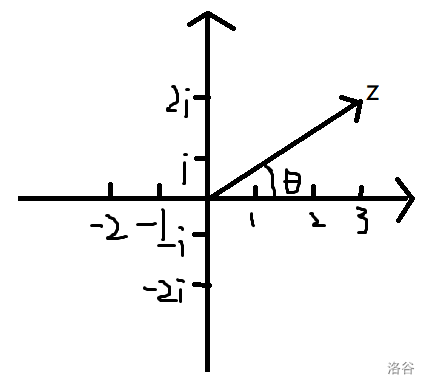
运算

复数的模

复数 $z=a+bi$ 的模为其复平面上对应的向量的长度记作 $|z|$。$|z|$ 的计算公式为

$$|z|=\sqrt{a^2+b^2}$$

可以理解为这个数就是复数 $z$ 到复平面上原点的距离。

共轭复数

复数 $z$ 的共轭复数是由 $z$ 沿着复平面实数轴（$x$ 轴）反转得到的，记为 $\overline{z}$。

$z$ 与 $\overline{z}$ 之间有以下的性质：

• 设 $z$ 的幅角为 $\theta_0$，$\overline{z}$ 的幅角为 $\theta_1$，则 $\theta_0+\theta_1=2\pi$。
• $|z|=|\overline{z}|$
• 若 $z=a+bi$，则 $\overline{z}=a-bi$。
• $z\cdot\overline{z}=(a+bi)(a-bi)=a^2-b^2i^2=a^2+b^2$，所以 $z\cdot\overline{z}$ 一定是个实数。

复数简单运算

假设有两个复数 $z_1=a_1+b_1i$ 和 $z_2=a_2+b_2i$。

$$z_1\pm z_2=(a_1\pm b_1i)+(a_2\pm b_2i)=(a_1\pm a_2)+(b_1\pm b_2)i\\ \\ z_1\times z_2=(a_1+b_1i)\times(a_2+b_2i)=a_1a_2+a_1b_2i+a_2b_1i+b_1b_2i^2\\ \because i^2=-1\\ \therefore z_1\times z_2=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i\\ \\ \frac{z_1}{z_2}=\frac{z_1\overline{z_2}}{z_2\overline{z_2}}=\frac{z_1\overline{z_2}}{(a_2+b_2i)(a_2-b_2i)}=\frac{z_1\overline{z_2}}{a_2^2+b_2^2}$$

设 $z_0=z_1\times z_2$。若 $\theta_0$ 为 $z_0$ 的幅角，$\theta_1$ 为 $z_1$ 的幅角，$\theta_2$ 为 $z_2$ 的幅角。则有以下这些性质

$$\theta_0=\theta_1+\theta_2\\ |z_0|=|z_1|\times|z_2|$$

若将上文的 $z_0$ 的值换为 $\frac{z_1}{z_2}$，则有以下这些性质

$$\theta_0=\theta_1-\theta_2\\ |z_0|=\frac{z_1}{z_2}$$

相当于几何意义下的复数相乘。具体证明先鸽一下......

三角函数

三角函数最初的定义是表示直角三角形三边比例关系的函数。

在直角三角形上确定角 $\theta$，则邻边、对边、斜边的定义如下：

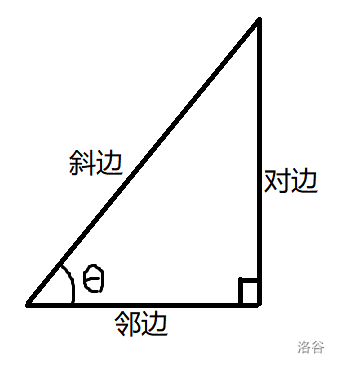
假设邻边长度为 $a$，对边长度为 $b$，斜边长度为 $c$。则三个三角函数的定义如下：

$$\sin\theta=\frac{b}{c}\\ \cos\theta=\frac{a}{c}\\ \tan\theta=\frac{\sin\theta}{\cos\theta}=\frac{b}{a}\\ $$

后来人们拓宽了三角函数的定义，把三角函数放到了单位圆上。就变成了这个样子：

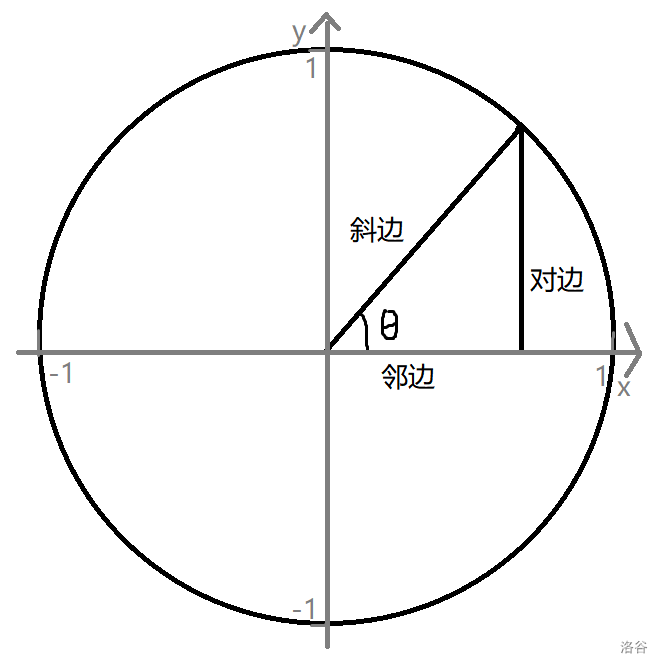
也就是说，$\theta$ 不一定要在 $0^\circ\sim 90^\circ$ 之间三角函数才有取值，在任意实数角度内都有值（包括负数）。但 $\tan$ 函数在 $90^\circ$ 及其整数倍数时是没有定义的。

根据两点间距离公式 $dis(a,b)=\sqrt{(X_a-X_b)^2+(Y_a-Y_b)^2}$，可以得出：

$$a^2+b^2=c^2\\ \frac{a^2}{c^2}+\frac{b^2}{c^2}=1\\ (\frac{a}{c})^2+(\frac{b}{c})^2=1\\ \cos^2 \theta+\sin^2 \theta=1$$

（此处 $a,b,c$ 与上文三边长度意思相同）

欧拉公式

我不会。

说白了就是 $e^{i\theta}=\cos\theta+i\sin\theta$。

可以用泰勒展开证明。

复数的单位根

单位根

若有未知数 $x$，则 $x^n=1$ 的解被称为单位根。这个方程的解在实数范围内最多只有两个，但在复数范围内有 $n$ 个，复数范围下的单位根也被称为单位复根。下面的问题与这个问题是等价的：

在复平面上，以原点为圆心，做半径为 $1$ 的圆也就是单位圆。将圆弧 $n$ 等分（第 $n$ 份与第 $1$ 份交界需交于实数轴正半轴上）。以原点为起点，$n$ 等分点为终点作 $n$ 个向量，设幅角为正且最小的向量对应的复数为 $\omega_n$，其余的 $n-1$ 个复数分别为 $\omega_n^2,\omega_n^3,\dots,\omega_n^n$。这里的 $n$ 个复数对应的就是上一个问题的 $n$ 个解。

如果将 $\omega_n,\omega_n^2,\dots,\omega_n^n$ 画在复平面上大概就是下图的样子（假设 $n=6$）：

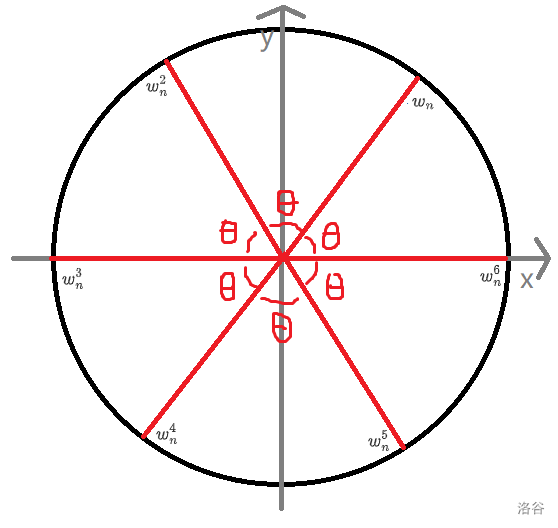
因为向量相乘，模长相乘，幅角向加。所以相邻两个向量间的模角相等。

---

单位根的三个小性质

• $\omega_n^n=1$
• $\omega_n^k=\omega_{dn}^{dk}(d\neq 0)$
• $\omega_{2n}{k+n}=-\omega_{2n}^{k}$

证明很容易，这里就不放证明了。

本原单位根

我们可以借助某些单位根来构造全体单位根，称这样的单位根为本原单位根。

$${\omega_n^k|0\leq k\leq n,\gcd(n,k)=1}$$

上述几何中的所有元素即为本原单位根。因为本原单位根对于任意的 $0<k<n$，都满足 $\omega_k\neq 1$，所以可以构造出所有单位根。

一共有 $\varphi(n)$ 个 $n$ 次本原原根。（显然）