树链剖分(轻/重链剖分学习笔记)
前置知识:LCA,树上dp。
前言
个人认为树链剖分是一个暴力数据结构,也就是它的本质就是暴力,只不过优化了一下而已。
树链剖分一般用于维护树上两点之间或子树中的权值。算是树上问题中较为基础的一个算法。
定义
轻/重链
对于树上的某个节点的所有子树中,如果这个儿子的所在的子树是这些子树中最大的(节点个数最多的),则称这个儿子为重儿子,其余的儿子则为轻儿子。除叶子节点外,所有节点都有恰好有一个重儿子,子树大小相同则取任意一个。
在这个树上连向重儿子的边叫做重边,其余的边叫做轻边。一段连续的重边连成的链叫做重链,下面给出一张图来解释一下:
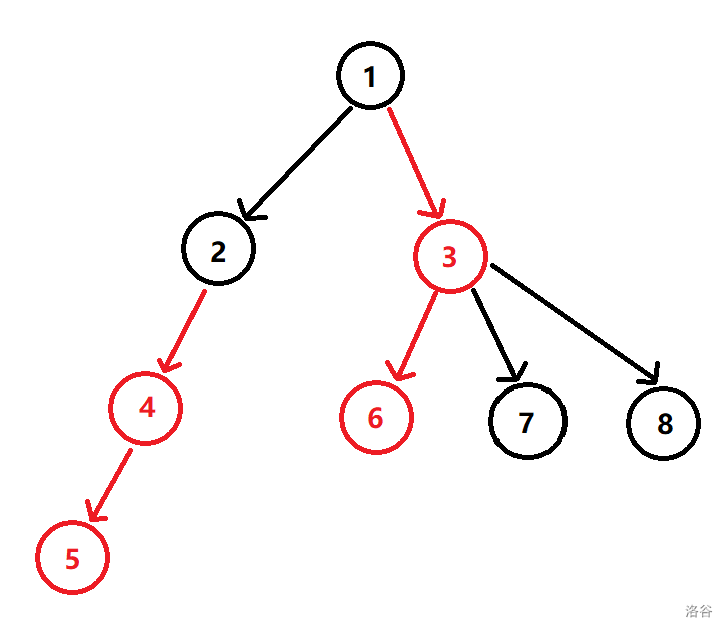
在这张图中,红色的节点为重儿子,黑色的节点为轻儿子,一段连续和红色的边即为重链。\(3,4,5,6\) 为重儿子,\(2,7,8\) 为轻儿子,\(1\) 为根节点(一般标记为轻儿子)。两个重链分别为 \(2\rightarrow 4\rightarrow 5\) 为一条重链,\(1\rightarrow 3\rightarrow 6\) 为另一条重链。一条重链总是在叶子节点结束(可以自己证明一下)。
dfn 序
dfn 序和前序遍历比较像,也是一种把树拍扁到序列上的一种算法。即对于每一个子树,先沿着一条链搜到底,再不断往上遍历其他节点。因为其遍历的方式,产生的序列有一个性质:任意一棵子树内的所有节点都在一段连续的区间上。

还是这张图,按照图中先左儿子再右儿子的遍历方法,其 dfn 序为 \([1,2,4,5,3,6,7,8]\)。这也是钦定先遍历重儿子再遍历轻儿子的 dfn 序。钦定先重儿子后有另一个性质:任意一条重链上的节点都在一段连续的区间上。
思想
树链剖分和很多暴力算法一样,是将某一部分整体处理,其他部分零散处理。
具体一些,就是在询问某两点之间的时候,如果有一部分在重链上,则使用这段预处理好的答案,其余部分暴击计算。
下文以P3384 【模板】重链剖分/树链剖分为例,讲一下具体怎么树剖。
根据上文的 dfn 序的性质,我们可以把这个树搬到线段树上处理,因为线段树可以处理区间问题,而 dfn 序则可以将树上问题转换为区间问题。(实际上树剖干的也是这件事)
于是我们可以将对链的操作分为以下几种情况:
- 这条链被一条重链所包含(这条链是一条重链):由于一条重链的所有点都在连续的一段区间内,所以直接对这个区间操作即可。
- 否则这条链可以被拆成若干条重链和其余不在重链上的节点,此时对于这些重链每一条分别进行操作,其余的点则进行单点操作。
至于对于整个子树的操作,由于一颗子树在连续一段区间内,直接对线段树操作即可。
具体内容看实现部分。
实现
树剖主要分为几个部分:第一次 dfs,第二次 dfs,具体操作。
第一次 dfs
主要处理每一个节点的父亲(具体操作用),找到重儿子,节点深度(具体操作用)。
void dfs1(int u,int fa)
{
fat[u]=fa;//父节点
siz[u]=1;//以u为根的子树的大小
dep[u]=dep[fa]+1;//节点深度
for(int v:g[u])
{
if(v==fa)
continue;
dfs1(v,u);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]])//更新重儿子
son[u]=v;//son[u]表示u的重儿子
}
}
第二次 dfs
由于第一次 dfs 已经找到了重儿子,那么这一次 dfs 中便获取 dfn 序以及重链。
void dfs2(int u,int fa,int tpf)
{
id[u]=++cnt;//dfn序
a[cnt]=w[u];//本题中线段树初值用
top[u]=tpf;//节点u所在重链中深度最小的节点
if(!son[u])//叶子节点
{
las[u]=cnt;//以u为根的子树的dfn序最大的节点的dfn序
//有一个性质是一个子树的根必定是这个子树里dfn序最小的
return;
}
dfs2(son[u],u,tpf);//优先搜索重儿子,继承这个节点的重链的父亲,所以tpf=tpf
for(int v:g[u])
{
if(v==fa||v==son[u])//注意重儿子已经被搜索过了
continue;
dfs2(v,u,v);//以v新开一条重链,所以tpf=v
}
las[u]=cnt;//同上
}
具体操作
链:
void updatepth(int x,int y,int k)//修改
{
while(top[x]!=top[y])//当两个节点已经跳到了同一条重链中,剩下的需要手动操作
{
if(dep[top[x]]>dep[top[y]])//跳lca
{
tr.pupdate(id[top[x]],id[x],k);//对当前位置与所在重链的顶端进行操作
x=fat[top[x]];
}
else
{
tr.pupdate(id[top[y]],id[y],k);//同上
y=fat[top[y]];
}
}
tr.pupdate(min(id[x],id[y]),max(id[x],id[y]),k);//x和y在一条重链内,剩余部分单独操作
}
int querypth(int x,int y)//查询,和修改差不多
{
int ans=0;
while(top[x]!=top[y])
{
if(dep[top[x]]>dep[top[y]])
{
ans=(ans+tr.pquery(id[top[x]],id[x]))%p;
x=fat[top[x]];
}
else
{
ans=(ans+tr.pquery(id[top[y]],id[y]))%p;
y=fat[top[y]];
}
}
ans=(ans+tr.pquery(min(id[x],id[y]),max(id[x],id[y])))%p;
return ans;
}
子树的话直接对对应区间操作即可。
全部代码
#include<iostream>
#include<vector>
using namespace std;
#define N 1000010
#define int long long
int n,m,r,p,u,v,opt,x,y,z,las[N],a[N],w[N],cnt,id[N],fat[N],siz[N],son[N],dep[N],top[N];
vector<int> g[N];
class sgtree//略微封装的线段树
{
public:
int n,a[4*N],laz[4*N];
void set(int w)
{
n=w;
for(int i=1;i<=4*n;i++)
a[i]=laz[i]=0;
}
void downtag(int o,int l,int r)
{
laz[o<<1]+=laz[o];
laz[o<<1]%=p;
laz[o<<1|1]+=laz[o];
laz[o<<1|1]%=p;
int mid=l+r>>1;
a[o<<1]+=(mid-l+1)*laz[o];
a[o<<1]%=p;
a[o<<1|1]+=(r-mid)*laz[o];
a[o<<1|1]%=p;
laz[o]=0;
}
void update(int o,int l,int r,int x,int y,int k)
{
if(l>y||r<x)
return;
if(l>=x&&r<=y)
{
a[o]+=(r-l+1)*k;
a[o]%=p;
laz[o]+=k;
laz[o]%=p;
return;
}
int mid=l+r>>1;
downtag(o,l,r);
update(o<<1,l,mid,x,y,k);
update(o<<1|1,mid+1,r,x,y,k);
a[o]=a[o<<1]+a[o<<1|1];
a[o]%=p;
}
int query(int o,int l,int r,int x,int y)
{
if(r<x||l>y)
return 0;
if(l>=x&&r<=y)
return a[o];
int mid=l+r>>1;
downtag(o,l,r);
int r1=query(o<<1,l,mid,x,y);
int r2=query(o<<1|1,mid+1,r,x,y);
return (r1+r2)%p;
}
void pupdate(int x,int y,int k)
{
update(1,1,n,x,y,k);
}
int pquery(int x,int y)
{
return query(1,1,n,x,y);
}
}tr;
void dfs1(int u,int fa)
{
fat[u]=fa;
siz[u]=1;
dep[u]=dep[fa]+1;
for(int v:g[u])
{
if(v==fa)
continue;
dfs1(v,u);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]])
son[u]=v;
}
}
void dfs2(int u,int fa,int tpf)
{
id[u]=++cnt;
a[cnt]=w[u];
top[u]=tpf;
if(!son[u])
{
las[u]=cnt;
return;
}
dfs2(son[u],u,tpf);
for(int v:g[u])
{
if(v==fa||v==son[u])
continue;
dfs2(v,u,v);
}
las[u]=cnt;
}
void updatepth(int x,int y,int k)
{
while(top[x]!=top[y])
{
if(dep[top[x]]>dep[top[y]])
{
tr.pupdate(id[top[x]],id[x],k);
x=fat[top[x]];
}
else
{
tr.pupdate(id[top[y]],id[y],k);
y=fat[top[y]];
}
}
tr.pupdate(min(id[x],id[y]),max(id[x],id[y]),k);
}
int querypth(int x,int y)
{
int ans=0;
while(top[x]!=top[y])
{
if(dep[top[x]]>dep[top[y]])
{
ans=(ans+tr.pquery(id[top[x]],id[x]))%p;
x=fat[top[x]];
}
else
{
ans=(ans+tr.pquery(id[top[y]],id[y]))%p;
y=fat[top[y]];
}
}
ans=(ans+tr.pquery(min(id[x],id[y]),max(id[x],id[y])))%p;
return ans;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>m>>r>>p;
tr.set(n);
for(int i=1;i<=n;i++)
{
cin>>w[i];
w[i]%=p;
}
for(int i=1;i<n;i++)
{
cin>>x>>y;
g[x].push_back(y);
g[y].push_back(x);
}
dfs1(r,0);
dfs2(r,0,r);
for(int i=1;i<=n;i++)
{
tr.pupdate(i,i,a[i]);//线段树初始化
}
for(int i=1;i<=m;i++)
{
cin>>opt;
if(opt==1)
{
cin>>x>>y>>z;
updatepth(x,y,z);
}
else if(opt==2)
{
cin>>x>>y;
cout<<querypth(x,y)<<"\n";
}
else if(opt==3)
{
cin>>x>>z;
tr.pupdate(id[x],las[x],z);//子树修改
}
else
{
cin>>x;
cout<<tr.pquery(id[x],las[x])<<"\n";//子树查询
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号