学习笔记：AC自动机

AC自动机是一种多模匹配算法 ,AC自动机常常用于多模式串，单文本串的匹配算法。

在此之前，你应当学会 KMP&Trie。

我们先给一组例子：

abcd
bcd
cd
d
ac
ad

这是这组例子建成的 Trie 树：

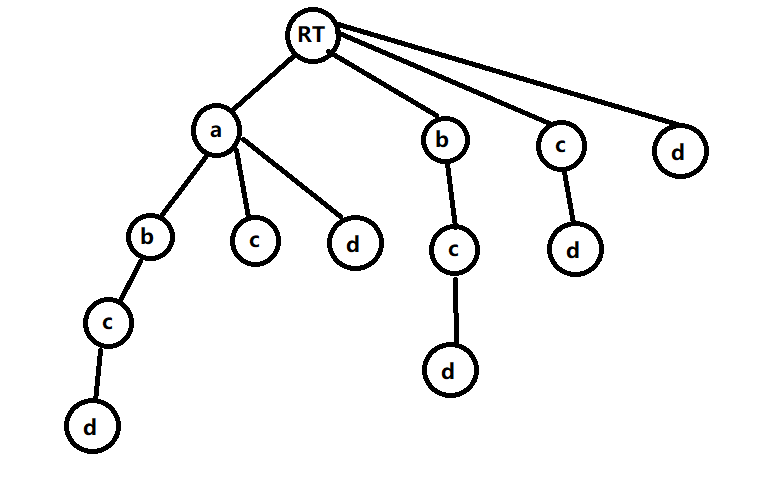
思想

AC自动机的核心思想： 如果当前模式串匹配成功部分的后缀与其他某个模式串的前缀一致，则如果在下一次匹配失败时，直接匹配那个模式串的与当前模式串的后缀不同部分。

举例： 模式串1 abcd，模式串2 bcf，模式串3 e。

如果文本串为 abce，与模式串1 abcd 已经匹配了 abc 的部分，则在匹配 e 时发现匹配失败，则直接匹配模式串2 bcf，由于 bc 部分在文本串1中已经匹配成功，则无需再次匹配，直接在模式串2中匹配 e。 e 匹配不成功，由于没有可以省去匹配前缀的模式串，则从头匹配。与模式串3 e 匹配成功。

注意：由于不一定要从文本串开头匹配模式串，所以舍去部分已经匹配的前缀。

不难发现，跳转到前缀与当前模式串已匹配部分后缀相同长度最长的的模式串一定是最优的，因为较长的后缀包含较短的后缀。

上面的跳转操作可以大大减少匹配次数，让我们把匹配失败时进行跳转操作的数组命名为 \(fail\) 数组。

\(fail_u\) 表示在 \(u\) 的子节点失配（即匹配失败）时， 应当继续匹配的位置的父节点 。

例如在上文的例子中，模式串1 abcd 匹配到 d 的位置匹配失败，应当继续匹配模式串2中的 f。模式串1中 d 的父亲为 c，模式串2中的 f 的父亲为 c，所以模式串1的 c 的 \(fail\) 指针应为模式串2中的 c。

---

让我们回到刚刚建好的那棵 Trie 树上，先从第一层开始建立 Trie 树。至于为什么按照深度建，因为一个节点的 \(fail\) 指针的指向的节点深度一定比这个节点的深度要浅。（不能深度大于是因为那样节省的串的长度比目前已匹配的长度还要长，显然是不合法的。如果深度一样那就是这个节点本身，显然是没有意义的。）

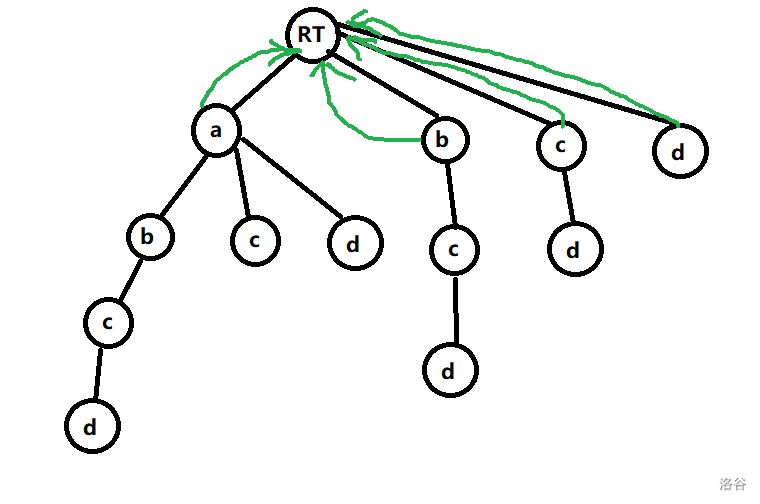
这是第一层节点的 \(fail\) 指针所指向的节点，不难发现全部指向了 RT。

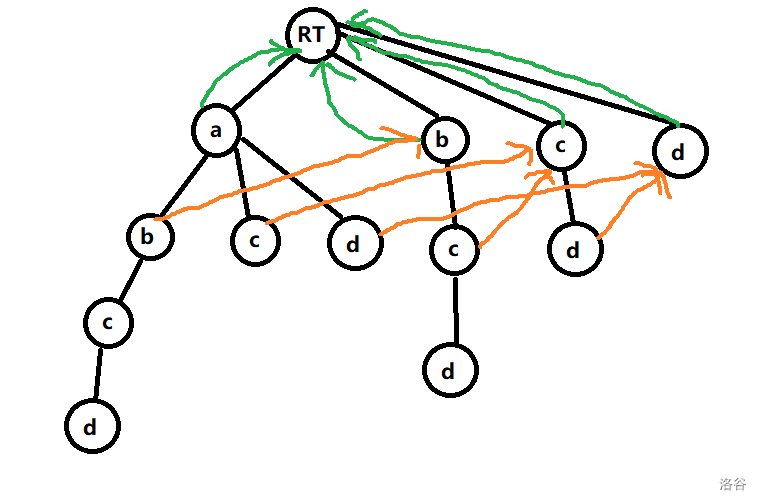
这是第二层节点的 \(fail\) 指针所指向的节点。不难发现如果一个节点的 \(fail\) 指针所指向的节点不是 RT 的话，指向的节点的值一定与这个节点的值一致。

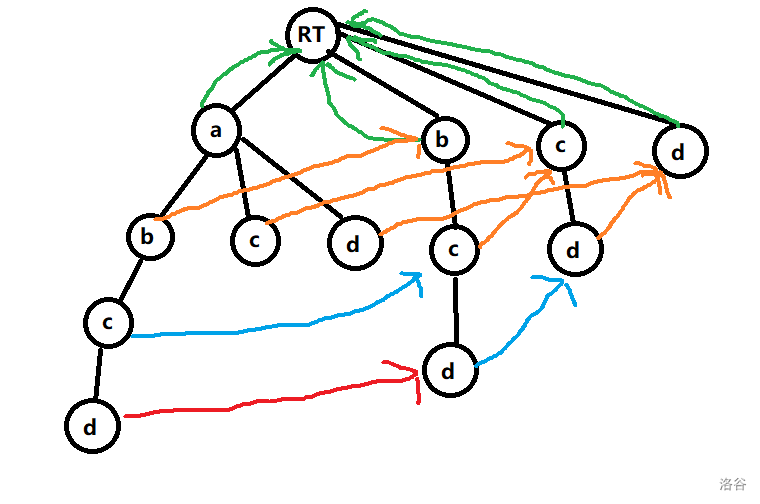
这是第三，四层节点的 \(fail\) 指针所指向的节点。不难发现沿着一个节点的 \(fail\) 指针走下去，一定会回到 RT。

实现

\(fail\) 指针的生成方法如下：

设 \(u\) 为当前节点，\(fail_u\) 为节点 \(u\) 的 \(fail\) 指针，\(v=tr_{u,ch}\) 为 \(trie\) 树上节点 \(u\) 的某个儿子 \(v\)。

• 如果 \(v\) 存在，则 \(fail_v=tr_{fail_u,ch}\)。

• 否则 \(v=tr_{fail_u,ch}\)。

感性理解，\(v\) 不存在时便直接跳到 \(fail\) 指针，因为失配了。

当 \(v\) 存在的时候，这个式子可以看作尝试将自己与失配串同时往外拓/加上字符 \(ch\)，如果失败，则跳到 \(fail\) 指针的 \(fail\) 指针，因为当 \(tr_{fa_u,ch}\) 不存在时，值为它的 \(fail\) 指针。这便是第二种操作的作用，可以巧妙递推构造 \(fail\) 指针。

正是因为如此，\(fail\) 指针构造时要按照节点深度转移，写起来像个 \(dp\)。

这是对于纯粹的匹配多个模式串的建 \(fail\) 指针的代码：

void getfail()
{
	queue<int> q;
	fail[1]=1;
	for(int i=0;i<26;i++)//q存储要转移到的fail指针，先从第一层节点递推
	{
		int o=trie[1][i];
		if(o)
		{
			fail[o]=1;
			q.push(o);
		}
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		int fa=fail[u];
		for(int i=0;i<26;i++)
		{
			int v=trie[u][i];
			if(v)
			{
				fail[v]=trie[fa][i];
				q.push(v);//继续推
			}
			else
			 trie[u][i]=trie[fa][i];
		}
	}
}

建议先理解以上代码再继续阅读。

而关于匹配部分，则沿着 \(trie\) 树往下走，遇到某个模式串的结尾便统计，和 \(kmp\) 有些类似。

以下是 P3808 【模板】AC 自动机（简单版） 的代码，部分解释放在注释里。

#include<iostream>
#include<string>
#include<queue>
using namespace std;
#define N 1000010
#define S 26
string s;
int n,cnt=1,trie[N][S],leaf[N],fail[N];
void insert(string s)//建trie树
{
	int o=1;
	for(int i=0;i<s.size();i++)
	{
		char ch=s[i];
		int v=trie[o][ch-'a'];
		if(!v)
		{
			trie[o][ch-'a']=++cnt;
		}
		o=trie[o][ch-'a'];
	}
	leaf[o]++;
}
void getfail()//建fail
{
	queue<int> q;
	fail[1]=1;
	for(int i=0;i<26;i++)
	{
		int o=trie[1][i];
		if(o)
		{
			fail[o]=1;
			q.push(o);
		}
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		int fa=fail[u];
		for(int i=0;i<26;i++)
		{
			int v=trie[u][i];
			if(v)
			{
				fail[v]=trie[fa][i];
				q.push(v);
			}
			else
			 trie[u][i]=trie[fa][i];
		}
	}
}
int query(string s)//匹配
{
	int o=1,ans=0;
	for(int i=0;i<s.size();i++)
	{
		char ch=s[i];
		o=trie[o][ch-'a'];//沿着trie树向下走，只需遍历trie数组
		int v=o;
		ans+=leaf[v];
		leaf[v]=0;//防止计重
	}
	return ans;
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>s;
		insert(s);
	}
	getfail();
	cin>>s; 
	cout<<query(s)<<endl;
}