实验三 查找和排序 实验报告 20162305
实验三 查找和排序 实验报告 20162305
一、查找和排序-1
1、实验要求
- 完成教材P302 Searching.Java ,P305 Sorting.java中方法的测试
不少于10个测试用例，提交测试用例设计情况（正常，异常，边界，正序，逆序），用例数据中要包含自己学号的后四位
提交运行结果图（可多张）
2、实验过程
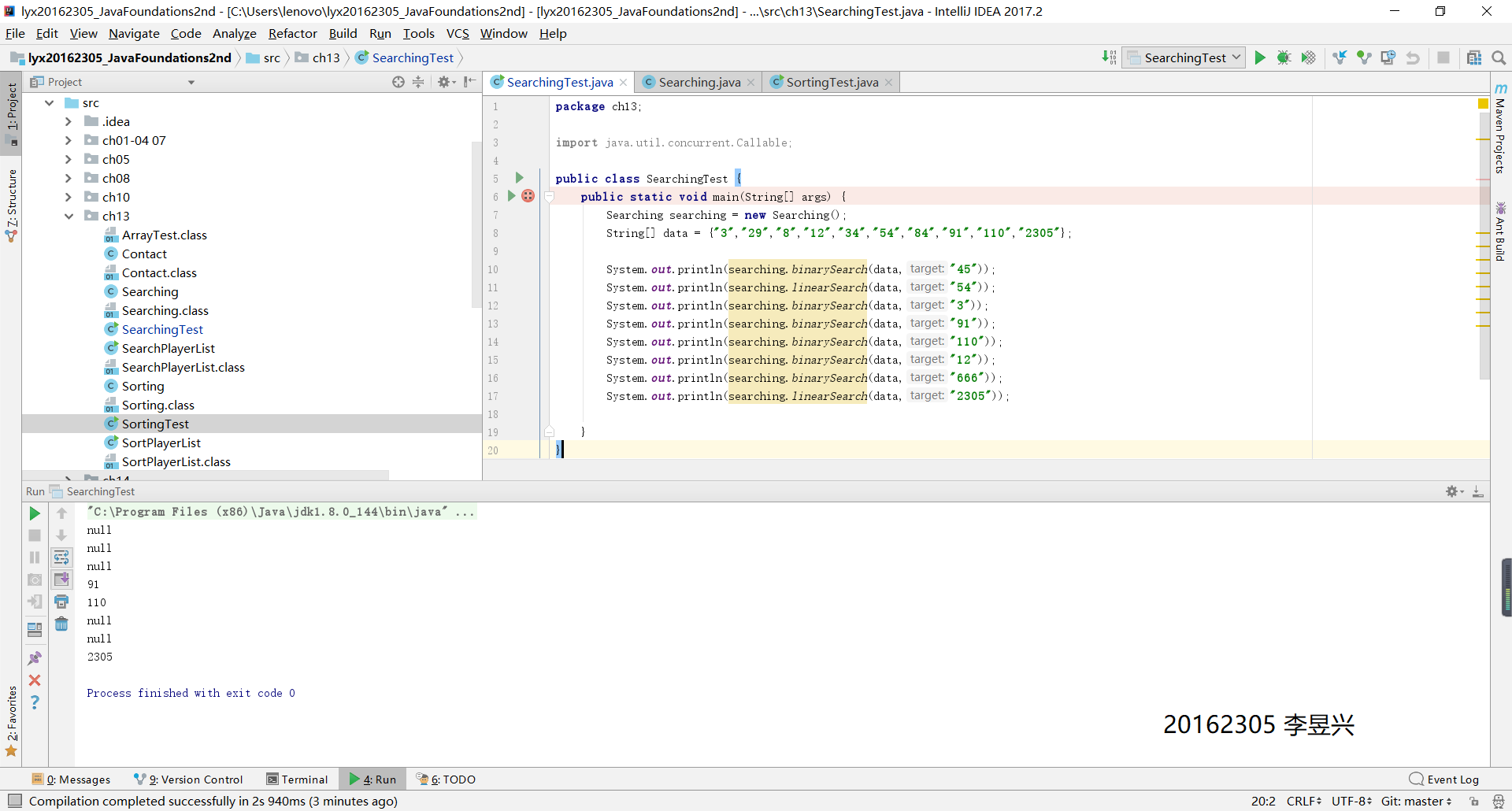
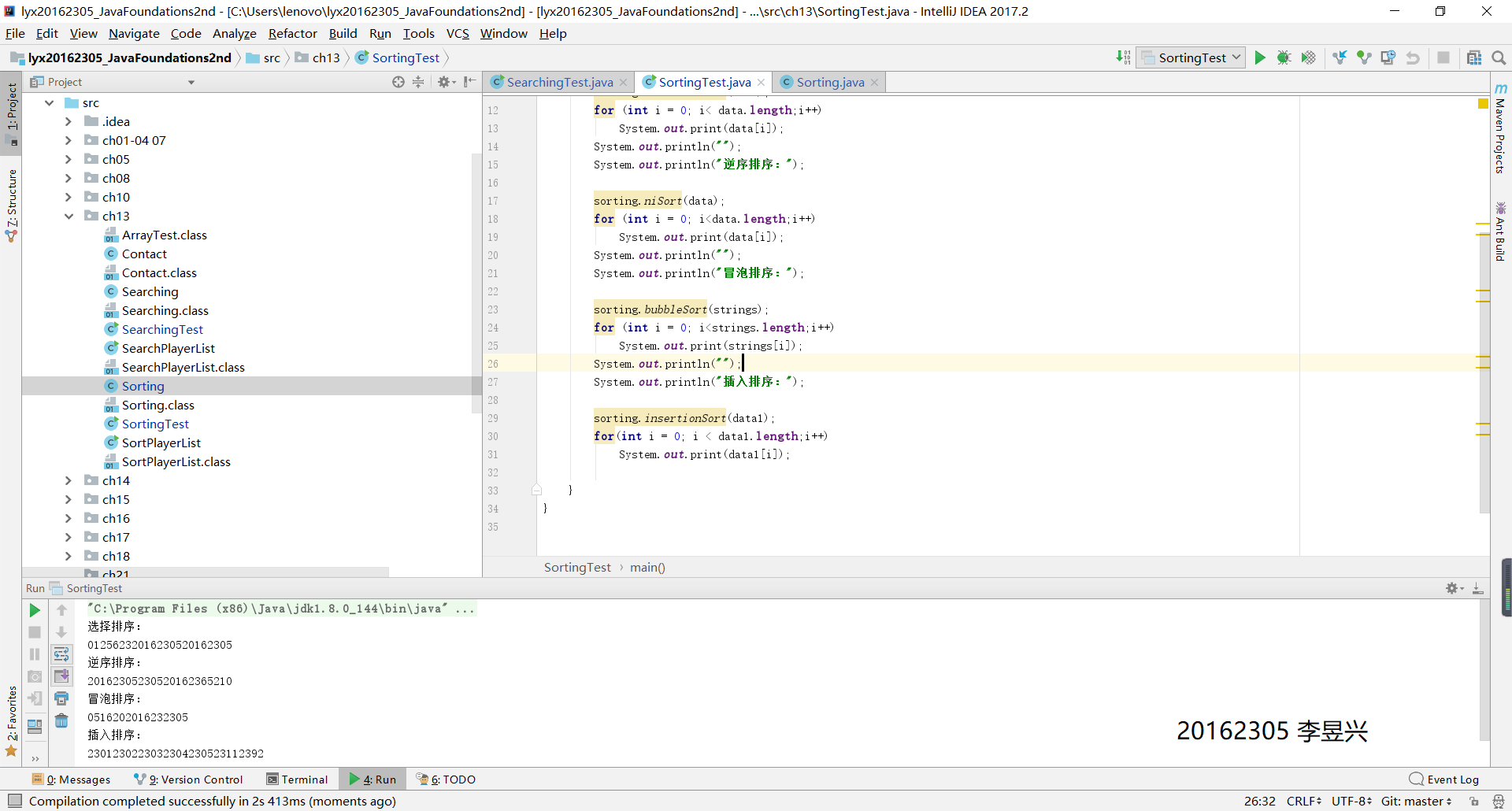
- 这个实验是在教材上的代码基础上实现的。教材中给了Searching类和Sorting类，测试这两个代码中给出的方法。查找类中包含了线性查找和二分查找两种方法。排序类中包含了像选择排序，插入排序，冒泡排序等等方法。这些方法在之前的学习中已经了解过，设计测试类，在两个类的测试类中一一实现这些方法。
3、实验成果截图
二、查找和排序-2
1、实验要求
- 重构你的代码
把Sorting.java Searching.java放入 cn.edu.besti.cs1623.（姓名首字母+四位学号） 包中
把测试代码放test包中
重新编译，运行代码，提交编译，运行的截图（IDEA，命令行两种）
2、实验过程
- 按照实验要求，我在IDEA中新建了一个package包，命名为cn.edu.besti.cs162305.lyx。在IDEA中重构代码，将代码加入相应的文件夹中，然后运行，在IDEA中可以实现。不过打开命令行后编译成功后，命令行中显示代码编译没问题，不过结果却没能显示出来。
3、实验成果截图
-
命令行
-
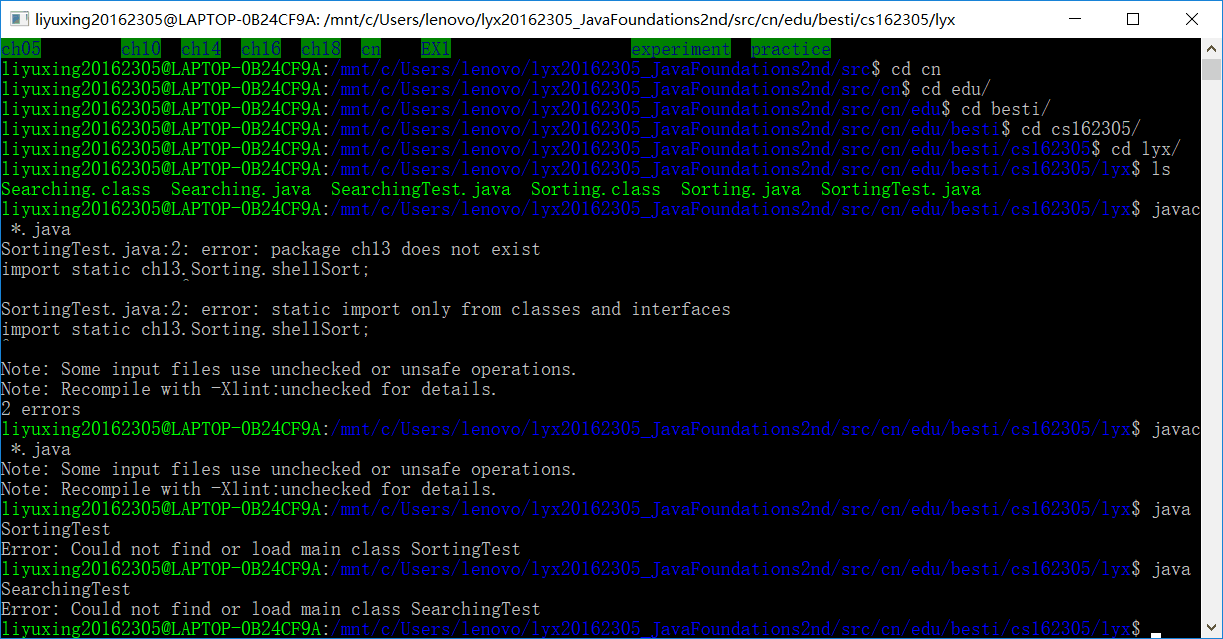
IDEA
-
1、
-
2、
三、查找和排序-3
1、实验要求
- 参考 查找算法博客 在Searching中补充查找算法并测试
提交运行结果截图
2、实验过程
- 在这篇学习博客中，一共提到了7种查找的方法，分别是顺序查找、二分查找、插值查找、斐波那契查找、树表查找、分块查找和哈希查找。其中的顺序查找和二分查找在教材的代码中都已经实现，下面介绍其他五种查找方法
（1）、插值查找
-
插值查找是基于二分查找算法，将查找点的选择改进为自适应选择，可以提高查找效率。当然，差值查找也属于有序查找。对于表长较大，而关键字分布又比较均匀的查找表来说，插值查找算法的平均性能比折半查找要好的多。
-
插值查找在实际使用时，一般要满足两个假设条件：
（1）每一次对数据的访问与通常的指令相比，费用都是相当昂贵的。例如，待查找的表一定是在磁盘而非内存中，因而每一次比较都
要进行磁盘访问。
（2）数据不仅是已被排好序的，而且呈现均匀分布特征。 -
实验代码
public static Comparable InsertionSearch(int[] num, int key) {
//定义三个判断数
int low, high, mid;
low = 0;
high = num.length - 1;
while (low <= high) {
// mid = (low + high) / 2;
//二分查找
mid = low + (high - low) * (key - num[low]) / (num[high] - num[low]); // 插值查找
if (key < num[mid]) high = mid - 1;
else if (key > num[mid]) low = mid + 1;
else
// 如果等于则直接还回下标值
return mid;
}
return -1;
}
（2）、斐波那契查找
-
斐波那契查找也是二分查找的一种提升算法，通过运用黄金比例的概念在数列中选择查找点进行查找，提高查找效率。同样地，斐波那契查找也属于一种有序查找算法。
-
相对于折半查找，一般将待比较的key值与第mid=（low+high）/2位置的元素比较，比较结果分三种情况：
1、相等，mid位置的元素即为所求
2、>，low=mid+1 3、<，high=mid-1。 -
斐波那契查找与折半查找很相似，他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1，及n=F(k)-1;开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1),比较结果也分为三种：
1、相等，mid位置的元素即为所求
2、low=mid+1,k-=2;
3、high=mid-1,k-=1。 -
说明：low=mid+1说明待查找的元素在[mid+1,high]范围内，k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个，所以可以递归的应用斐波那契查找。
-
实验代码
private int max_size = 20;//斐波那契数组的长度
/*构造一个斐波那契数组*/
public void Fibonacci(int[] F) {
F[0] = 0;
F[1] = 1;
for (int i = 2; i < max_size; ++i)
F[i] = F[i - 1] + F[i - 2];
}
/*定义斐波那契查找法*/
int FibonacciSearch(int[] a, int key) //a为要查找的数组,n为要查找的数组长度,key为要查找的关键字
{
int low = 0;
int high = a.length - 1;
int[] F = new int[max_size];
Fibonacci(F);//构造一个斐波那契数组F
int k = 0;
while (a.length > F[k] - 1)//计算n位于斐波那契数列的位置
++k;
//将数组a扩展到F[k]-1的长度
int[] temp = new int[F[k] - 1];
for (int i = 0; i < a.length; i++)
temp[i] = a[i];
for (int i = a.length; i < F[k] - 1; ++i)
temp[i] = a[a.length - 1];
while (low <= high) {
int mid = low + F[k - 1] - 1;
if (key < temp[mid]) {
high = mid - 1;
k -= 1;
} else if (key > temp[mid]) {
low = mid + 1;
k -= 2;
} else {
if (mid < a.length) return mid; //若相等则说明mid即为查找到的位置
else return a.length - 1; //若mid>=n则说明是扩展的数值,返回n-1
}
}
return 0;
}
（3）、二叉树查找
- 实现这个方法相对简单。我们可以利用之前实现过的二叉查找树来实现查找功能。定义一个二叉查找树，遍历整个数，利用二叉查找树中的find方法来查找目标值，从而实现查找功能。
- 实验代码
public int BinaryTreeSearch(int[] a, int key) {
LinkedBinarySearchTree linkedBinarySearchTree = new LinkedBinarySearchTree();
//添加元素进入查找树
for (int i = 0; i < a.length; i++)
linkedBinarySearchTree.add(a[i]);
//利用find方法查找值
if (linkedBinarySearchTree.find(key) == null) return Integer.parseInt(null);
else return key;
}
（4）、分块查找
-
分块查找又称索引顺序查找，它是顺序查找的一种改进方法。将n个数据元素"按块有序"划分为m块（m ≤ n）。每一块中的结点不必有序，但块与块之间必须"按块有序"；即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字；而第2块中任一元素又都必须小于第3块中的任一元素，以此类推。
-
实验代码
public static int blockSearch(int[] index, int[] a, int key, int m) {
// 在序列a数组中，用分块查找方法查找关键字为key的记录
// 1.在index[ ] 中折半查找，确定要查找的key属于哪个块中
int i = binarySearch(index, key);
if (i >= 0) {
int j = i > 0 ? i * m : i;
int length = (i + 1) * m;
// 在确定的块中用顺序查找方法查找key
for (int k = j; k < length; k++) {
if (key == a[k]) {
System.out.println("查询成功");
return k;
}
}
}
return -1;
}
（5）、哈希查找
- 利用Java中的HashMap类实现查找功能。其实现过程和二叉查找树实现查找类似。利用HashMap中的put方法将元素添加入表中，再用containKey方法判断有无目标元素，从而实现查找功能。
- 实验代码
public int HashSearch(int[] a , int key){
HashMap<Integer,Integer> hashMap = new HashMap();
for(int i = 0;i <a.length;i++)
hashMap.put(i,a[i]);
if(hashMap.containsKey(key) == true)
return key;
else
return 0;
}
3、实验成果截图
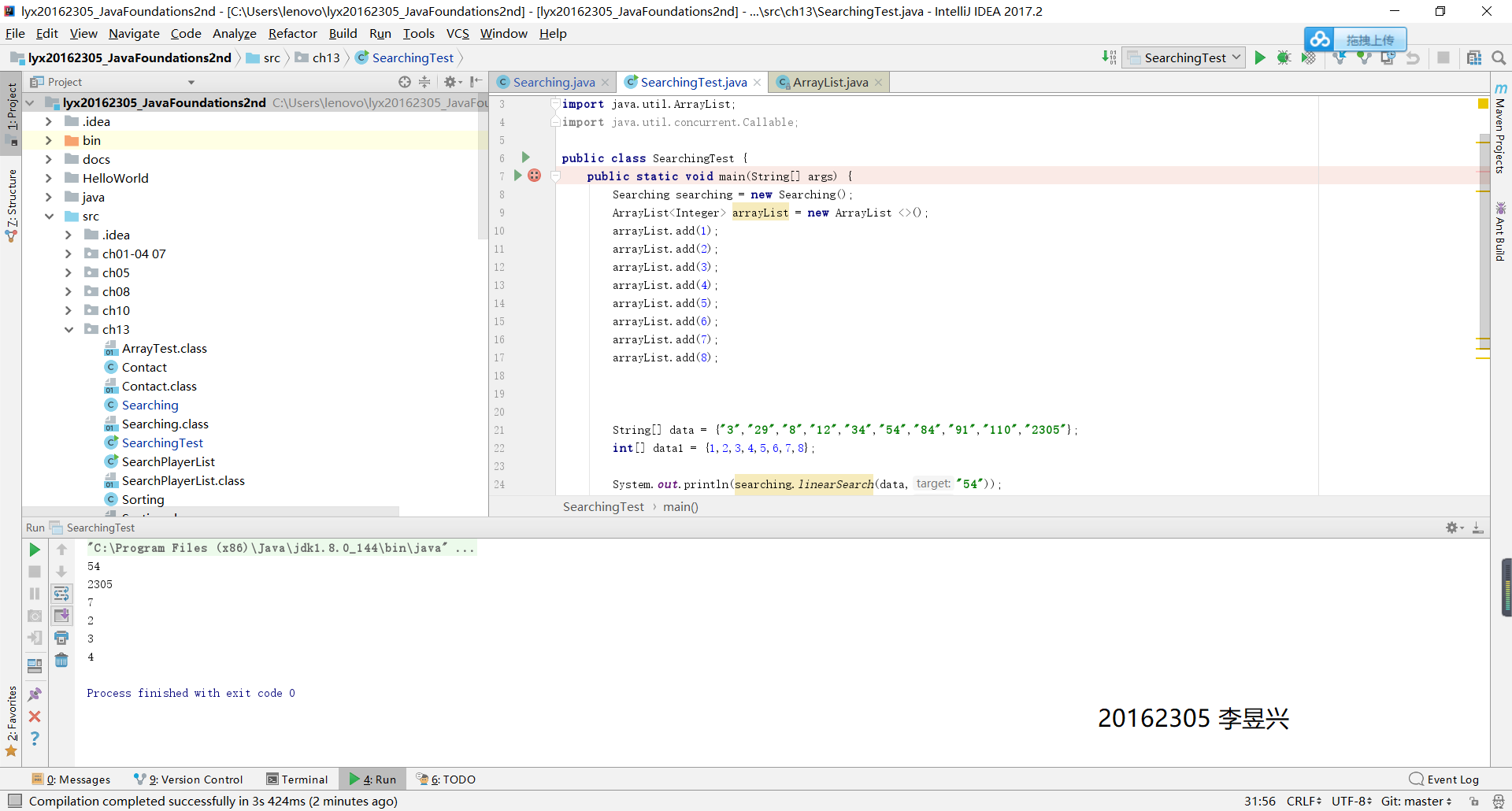
四、查找和排序-4
1、实验要求
- 补充实现课上讲过的排序方法：希尔排序，堆排序，桶排序，二叉树排序等。测试实现的算法（正常，异常，边界），提交运行结果截图，推送相关代码到码云上
2、实验过程
（1）、希尔排序
- 希尔排序的思想是先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量 =1( < …<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。
- 实验代码
public static void shellSort(int[] data) {
int j = 0;
int temp = 0;
for (int a = data.length / 2; a > 0; a /= 2) {
for (int i = a; i < data.length; i++) {
temp = data[i];
for (j = i - a; j >= 0; j -= a) {
if (temp < data[j]) {
data[j + a] = data[j];
} else {
break;
}
}
data[j + a] = temp;
}
for (int i = 0; i < data.length; i++)
System.out.print(data[i] + " ");
}
}
（2）、堆排序
- 利用之前完成的LinkedMaxHeap实现排序功能。根据最大堆的性质依次返回值并打印出来，实现排序功能
- 实验代码
public void heapSort(Comparable[] data){
LinkedMaxHeap linkedMaxHeap = new LinkedMaxHeap();
for (int i = 0; i < data.length; i++)
linkedMaxHeap.add(data[i]);
for (int i = data.length-1; i>=0;i--)
data[i]=linkedMaxHeap.removeMax();
}
（3）、桶排序
-
桶排序的基本思想是将一个数据表分割成许多buckets，然后每个bucket各自排序，或用不同的排序算法，或者递归的使用bucket sort算法。基本流程是先建立一堆buckets，再遍历原始数组，并将数据放入到各自的buckets当中，对非空的buckets进行排序； 按照顺序遍历这些buckets并放回到原始数组中即可构成排序后的数组。
-
实验代码
public static void bucketSort(int[] arr){
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int i = 0; i < arr.length; i++){
max = Math.max(max, arr[i]);
min = Math.min(min, arr[i]);
}
//桶数
int bucketNum = (max - min) / arr.length + 1;
ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
for(int i = 0; i < bucketNum; i++){
bucketArr.add(new ArrayList<Integer>());
}
//将每个元素放入桶
for(int i = 0; i < arr.length; i++){
int num = (arr[i] - min) / (arr.length);
bucketArr.get(num).add(arr[i]);
}
//对每个桶进行排序
for(int i = 0; i < bucketArr.size(); i++){
Collections.sort(bucketArr.get(i));
}
}
（4）、二叉树排序
- 利用二叉查找树的性质实现排序功能，利用类中findMin（）方法将数组中的元素排序。
- 实验代码
public static void BinaryTreeSort(Comparable[] a){
LinkedBinarySearchTree linkedBinaryTree = new LinkedBinarySearchTree();
for (int i = 0; i < a.length; i++)
linkedBinaryTree.add(a[i]);
for (int i = 0; i < a.length; i++) {
a[i] = linkedBinaryTree.findMin();
linkedBinaryTree.remove(linkedBinaryTree.findMin());
}
}
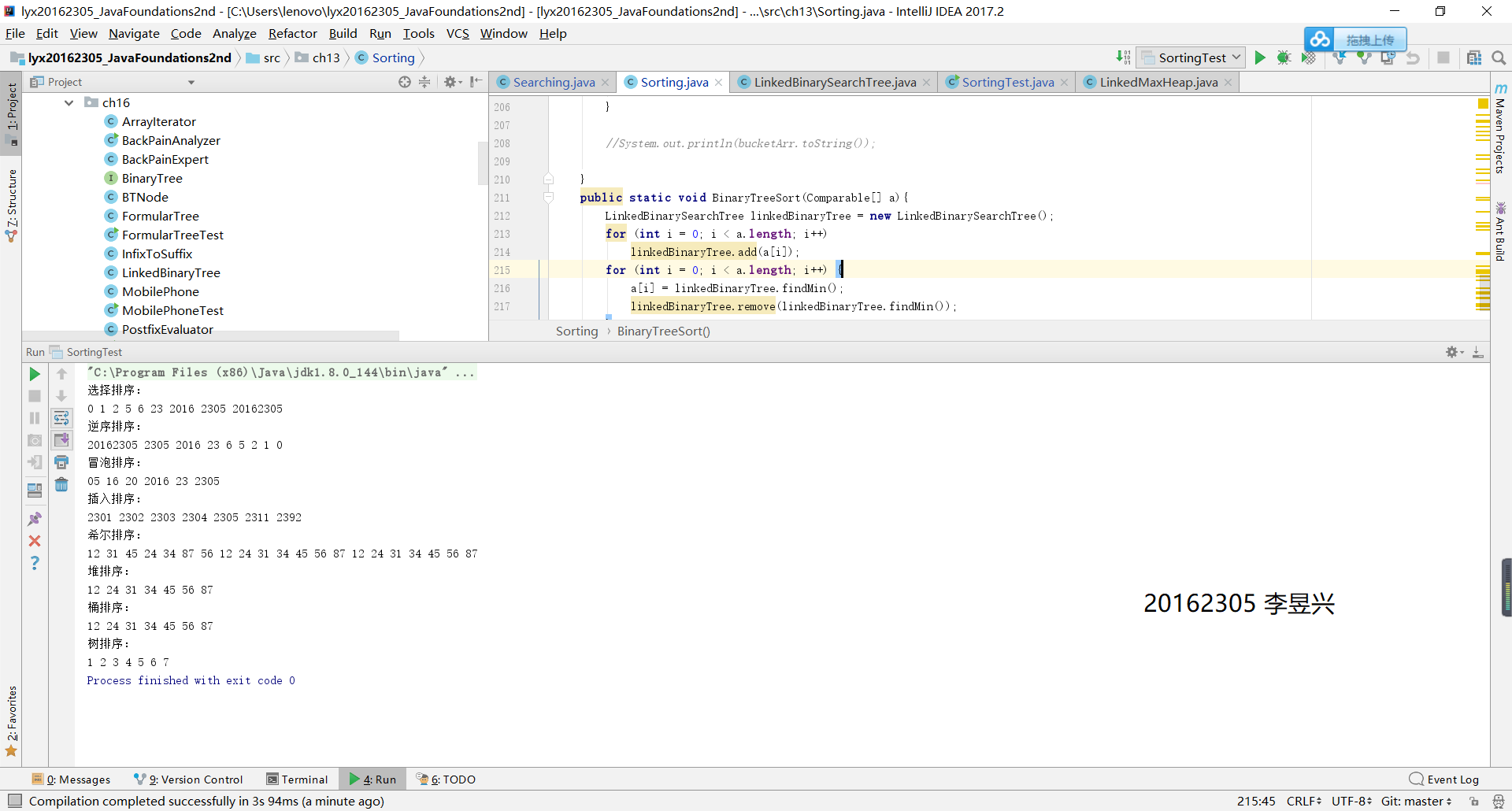
3、实验成果截图
