算法学习--广度优先搜索和深度优先搜索

一、广度优先搜索BFS

1.1、相关概念

1.图的遍历： 从图中某一顶点出发，按照某种搜索方法沿着图中的边对图中的所有节点访问一次且仅访问一次

1.2、算法流程

• 首先访问起始顶点 v ;
• 接着由出发依次访问 v 的各个未被访问过的邻接顶点 \(w_1,w_2,...,w_i\) ;
• 然后以此访问 \(w_1,w_2,...,w_i\) 的所有未被访问过的邻接顶点；
• 再从这些访问过的顶点出发，访问它们所有未被访问过的邻接顶点；
• ......, 以此类推；

方法：队列 + 辅助标记数组（标记节点是否被访问过）

1.3、算法实现过程图示

• 初始化数组和队列，0表示为未被访问过

• 将结点 1 入队，并修改标记数组中对应的0位置的值为1(表示结点1已经被访问过)

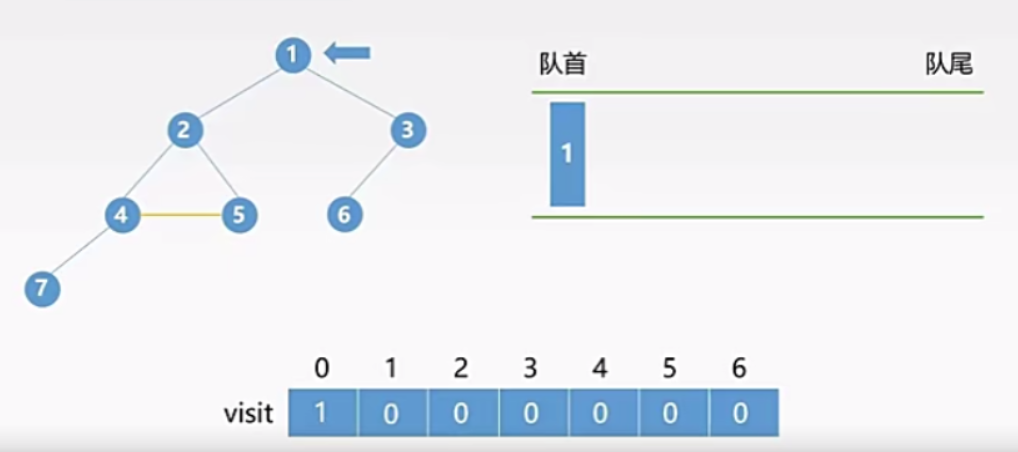
• 将队首元素 1 出队，并将它的所有未被访问的邻接结点(要求辅助标记为0)入队，并修改相应辅助数组下标的值

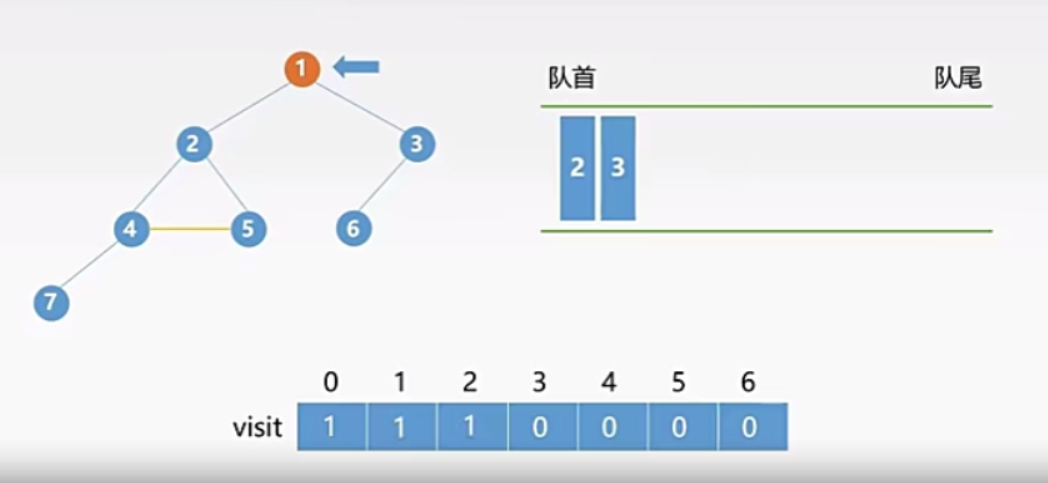
• 依次类推......

1.4、算法实现

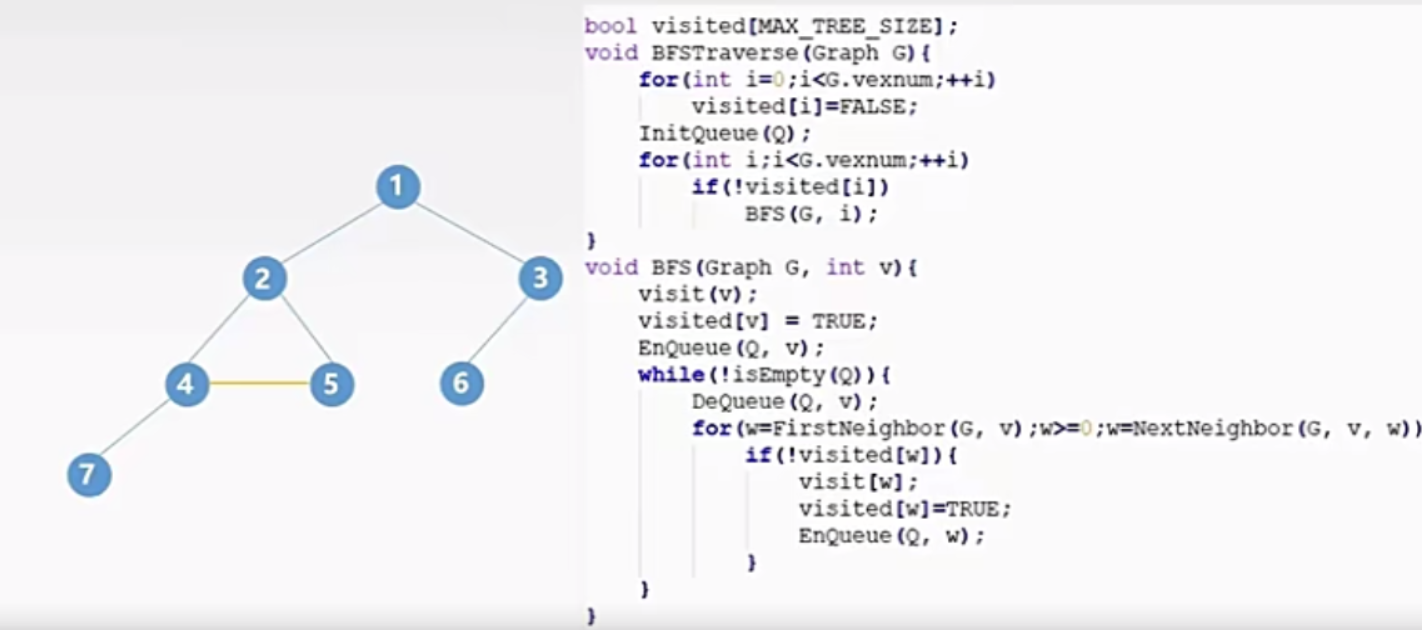
1.5、算法性能分析

• 空间复杂度： \(O(|V|)\) , 即顶点的数量大小（队列和辅助数组用到的空间大小都是顶点的数量大小）
• 时间复杂度：取决于找邻接顶点的方法

邻接矩阵法的DFS(BFS)序列唯一，邻接表法的不唯一

二、深度优先搜索DFS

2.1、算法流程

• 首先访问起始顶点 v ；
• 接着由 v 出发访问 v 的任意一个邻接且未被访问的邻接顶点 \(w_i\);
• 然后再访问与 \(w_i\) 邻接且未被访问过的任意顶点 \(y_i\);
• 若 \(w_i\) 没有邻接且未被访问的顶点时，就退回到它的上一层顶点 v ;
• 重复上诉过程，知道所有的顶点被访问完为止。

方法：栈 + 辅助标记数组

2.2、算法实现

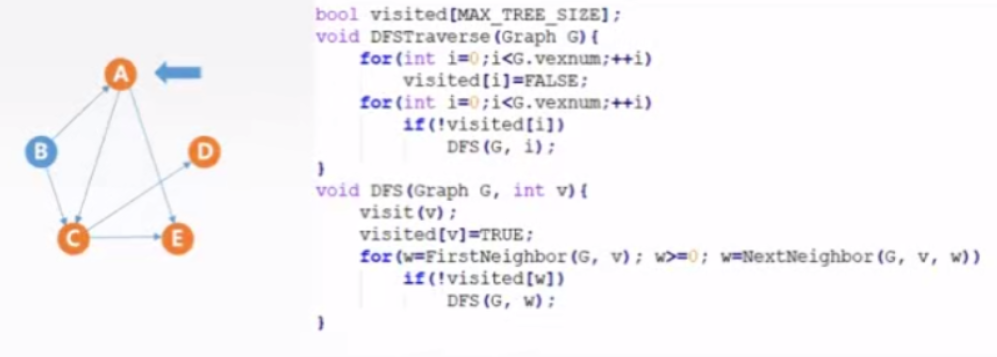
2.3、算法性能分析

• 空间复杂度： \(O(|V|)\) , 即顶点的数量大小（工作栈和辅助数组用到的空间大小都是顶点的数量大小）
• 时间复杂度： 根据找邻接结点的方式而定

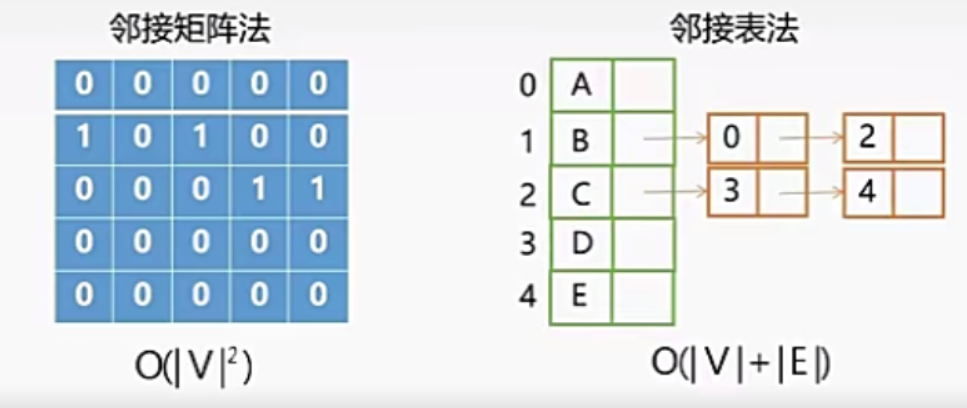
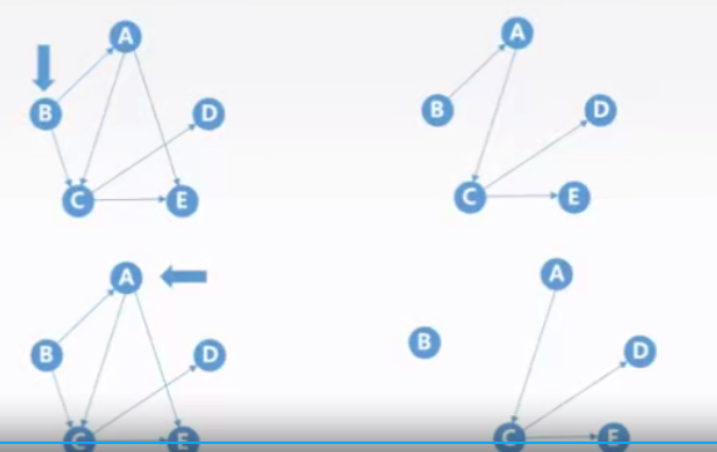
2.4、如何通过遍历来判断连通性

• 在无向图当中，在任意结点出发进行一次遍历 (调用一次BFS或者DFS)，若能访问全部结点，说明该无向图是连通的；
• 在无向图中，调用遍历函数(BFS或者DFS) 的次数为连通分量的个数；
• 针对有向图，上述结论不成立：因为有向图是有方向的，从一个顶点出发不一定能返回来，但是无向图可以。

三、应用

3.1、1302. 层数最深叶子节点的和

• 题目链接：https://leetcode.cn/problems/deepest-leaves-sum/
• 题目描述: 给你一棵二叉树的根节点 root ，请你返回层数最深的叶子节点的和 。
• 示例：
  

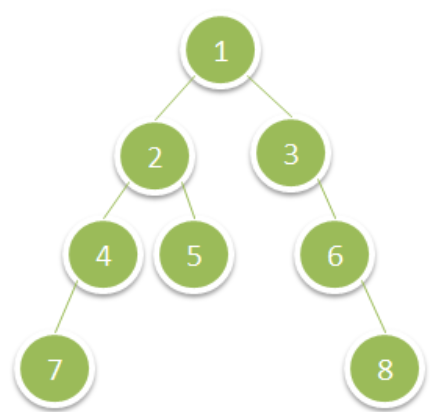
输入：root = [1,2,3,4,5,null,6,7,null,null,null,null,8]
输出：15

• 题解一：广度优先搜索

  • 题目分析：使用广度优先搜索对二叉树进行层序遍历时，不需要维护最大层数，只需要确保每一轮遍历的节点是同一层的全部节点，则最后一轮遍历的节点就是全部的叶子节点

  • 算法步骤：

    1. 将根节点加入队列，此时队列中只有一个节点，是第0层的全部节点；
    2. 每一轮遍历时，首先得到队列中的节点个数size，然后循环遍历这size个节点，这size个节点就是同一层的全部节点，记作x层；遍历时，第 x 层的每个节点的子节点都在第 x + 1 层，将子节点加入队列，则该轮遍历结束之后，第 x 层的节点全部从队列中取出，第 x + 1层的节点全部加入队列，队列中的节点是同一层的全部节点；
    3. 重复步骤2，直至队列为空。

  • 算法实现

    # Definition for a binary tree node.
    # class TreeNode:
    #     def __init__(self, val=0, left=None, right=None):
    #         self.val = val
    #         self.left = left
    #         self.right = right
    
    class Solution:
        def deepestLeavesSum(self, root: Optional[TreeNode]) -> int:
          q = deque([root]) # 创建队列，并入队根节点
          
          while q: # 当队列不为空时，执行循环体
            ans = 0	# 用于保存每一层所有节点的和
            for _ in range(len(q)): # 先计算队列长度，代表该层有多少个节点，循环就执行几次
              node = q.popleft()
              ans += node.val 
              if node.left:
                q.append(node.left)
              if node.right:
                q.append(node.right)
           return ans
    

  • 复杂度分析

    • 时间复杂度：O(n), 其中 n*n 是二叉树的节点数。广度优先搜索需要遍历每个节点一次。
    • 空间复杂度：O(n), 空间复杂度主要取决于队列空间，队列中的节点个数不超过 n个。

• 题解二：深度优先搜索

  • 题目分析：由于层数最深的节点一定是叶节点，因此只要找到所有层数最深的节点并计算节点值之和即可。使用深度优先搜索从根节点开始遍历整个二叉树，遍历每个节点时需要记录该节点的层数，规定根节点在第 0层。遍历过程中维护最大层数与最深节点之和。

  • 算法步骤：

    1. 判断当前节点的层数与最大层数的关系：

       • 如果当前节点的层数大于最大层数，则之前遍历到的节点都不是层数最深的节点，因此用当前节点的层数更新最大层数，并将最深节点之和更新为当前节点值；

       • 如果当前节点的层数等于最大层数，则将当前节点值加到最深节点之和。

    2. 对当前节点的左右子节点继续深度优先搜索。

  • 算法实现

    class Solution:
        def deepestLeavesSum(self, root: Optional[TreeNode]) -> int:
          maxLevel, ans = -1, 0
          def dfs(node: Optional[TreeNode], level: int) -> None:
            if node is None:  # 递归回退条件
              return 
            nonlocal maxLevel, ans  # 声明为全局变量
            if level > maxLevel:
              maxLevel, ans = level, node.val
            elif level == maxlevel:
              ans += node.val
            dfs(node.left, level + 1)
            dfs(node.right, level + 1)
          
          dfs(root, 0)
          return ans
          
    

  • 复杂度分析: 同广度优先搜索

  总结：使用广度优先搜索可以遍历每一层的所有节点，使用深度优先搜索可以找到最深层数！

  3.2、226. 翻转二叉树

• 题目描述： 给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

• 示例：

  输入：root = [4,2,7,1,3,6,9]
  输出：[4,7,2,9,6,3,1]
  

• 题解一：深度优先搜索

  • 题目分析：将题目的 输入 和 输出画成二叉树的形式一对比，可以发现输出的左右子树的位置跟输入正好是相反的，于是可以递归的交换左右子树来完成这道题。

  • 算法步骤：

    • 终止条件：当前节点为 null 时返回
    • 交换当前节点的左右节点，再递归的交换当前节点的左节点，递归的交换当前节点的右节点

  • 算法实现：

    # Definition for a binary tree node.
    # class TreeNode:
    #     def __init__(self, val=0, left=None, right=None):
    #         self.val = val
    #         self.left = left
    #         self.right = right
    class Solution(object):
    	def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
    		# 递归函数的终止条件，节点为空时返回
    		if not root:
    			return None
    		# 将当前节点的左右子树交换
    		root.left,root.right = root.right,root.left
    		# 递归交换当前节点的 左子树和右子树
    		self.invertTree(root.left)
    		self.invertTree(root.right)
    		# 函数返回时就表示当前这个节点，以及它的左右子树
    		# 都已经交换完了		
    		return root
    

  • 复杂度分析：

    • 时间复杂度：O(n)
    • 空间复杂度：最坏情况下是函数调用的深度O(h) , h是树的深度

• 题解二：广度优先搜索

  • 题目分析：广度优先遍历需要额外的数据结构--队列，来存放临时遍历到的元素。所以，我们需要先将根节点放入到队列中，然后不断的迭代队列中的元素。

  • 算法步骤：

    • 对当前节点调换其左右子树，然后判断其左子树是否为空，不为空就放入队列中；判断其右子树是否为空，不为空就放入队列中

  • 算法实现：

    class Solution(object):
    	def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        # 先判断树是否为空树
        if not root:
          return root
        
        queue = collections.deque([root])
        while queue:
          node = queue.popleft()
          # 交换当前节点的左右子树 就算是空树也可以交换
          node.left, node.right = node.right, node.left
          # 如果当前节点的左子树不为空，则放入队列等待后续处理
          if node.left:
            queue.append(node.left)
          # 如果当前节点的右子树不为空，则放入队列等待后续处理
          if node.right:
            queue.append(node.right)
         
        return root
          
    

  • 复杂度分析：

    • 时间复杂度：O(n)
    • 空间复杂度：O(n)

总结：深度优先遍历特点是一条路走到黑不行再退回来，广度优先的特点是一层一层的遍历