2022-IA-GCN: Interactive Graph Convolutional Network for Recommendation阅读笔记

IA-GCN: Interactive Graph Convolutional Network for Recommendation

0.论文信息

• paper地址：https://arxiv.org/pdf/2204.03827v1.pdf
• code：未公开

1. 摘要

• 问题： 在之前的研究工作中，在embedding过程中没有考虑user-item之间的交互特征

• 方法： 提出了IA-GCN模型，在user-item之间建立双边交互指导。

  • 在学习用户(user)表示的时候，注重在 item 树中给跟目标用户相似的邻居分配更多的权重。
  • 在学习项目(item)表示时，更关注在 user 树中与目标 item 相似的邻居。

  注：这篇文章是基于何向南老师的 Light-GCN 改的

  ---

2. 引言

问题： 有的基于gcn的CF算法虽然已经被广泛研究，但大多存在一个关键的限制：在CF层中，用户树和项目树直到最终融合时才进行交互。这是因为它们的聚合大多继承自传统的GCNs，，最初是为了对每个节点进行分类而提出的。然而，推荐任务与分类任务有着根本的不同: 不仅关注user和item的一般特征、用户的购买力、对项目的评分，还需要关注user和item之间的交互信息。比如: user 在选择 item 时的 consideration，item 吸引 user 的 characteristic，这些都决定着用户的 preference。

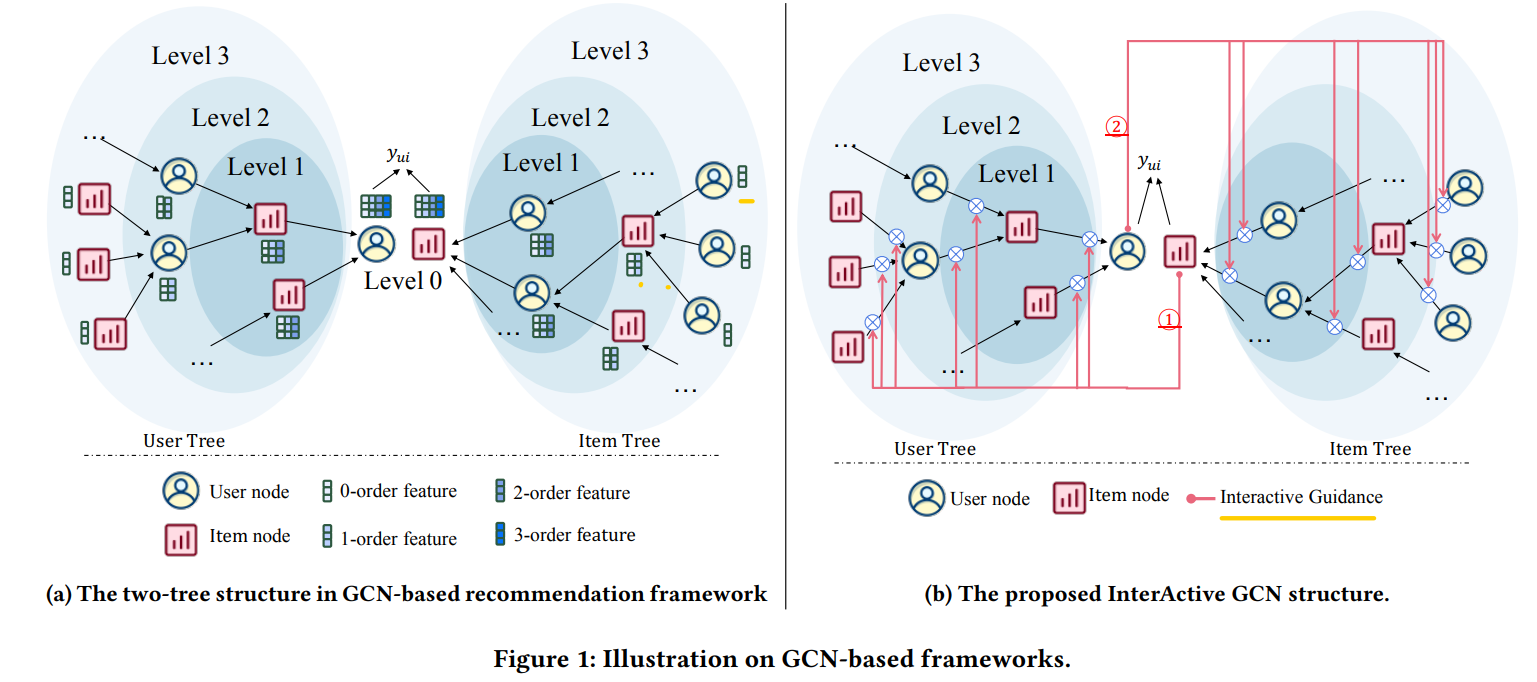
3. 模型概述

3.1 问题定义

• user：\(U=\{u_1,u_2,...,u_n\}\)
• item: \(I=\{i_1,i_2,...,i_m\}\)
• 目标是学得一个函数：\(f:U\times I ->R\) 来预测的user-item pair $ (u,i)$ 偏好分数 (preference score) \(\hat y_{u,i}\)
  • 一个准确的predictor \(f\) 应该给positive user-item pair $ (u,i_+)$ 分配相比于negative user-item pair $ (u,i_-)$ 更高的分数
  • positive 交互：点击、购买等等
• 根据 Bayesian Personalized Ranking (BPR)[1205.2618.pdf (arxiv.org)] , 将目标函数定义为：

\[l(D)=- \frac 1{|D|}\sum_{(u,i_+,i_-)\in D}ln \sigma(\hat y_{u,i_+}- \hat y_{u,i_-}+\lambda R ) \space \space \space \space \space \space \space \space \space \space \space \space \space （1） \]

​ \(D\) 是数据集，\(\sigma\) 是 \(sigmoid\) 函数，\(\lambda R\) 表示对所有模型参数的正则化。

• 偏好得分 \(\hat y_{u,i}\) 的计算，即目标用户和目标项目的内积：

\[\hat y_{u,i} =f(u.i)=<e^0_u,e^0_i> \space \space \space \space \space \space \space \space \space \space \space \space \space （2） \]

\(e_u^0 ,e_i^0\in R^d\) 是 \(u\) 和 \(i\) 的 embeddings，总的来说，我们有 $𝑚 + 𝑛 $ 嵌入向量，它们将与其他模型参数一起随机初始化和端到端训练。

3.2 图卷积框架

• 将用户-项目交互被表述为无向二分图 \(G=(V,E)\), 其中用户和项目都充当图节点，即$ V = U ∪ I$ 。$ 𝑢 - 𝑖 $ 交互作为边，即 \(E ⊆ U × I\)。

• 高阶特征表示为$ e^𝑘_𝑢, e^𝑘_𝑖, 𝑘 ∈ {1, ..., 𝐾}$，其中 𝑘 阶特征 \(e^𝑘_𝑢 /e^𝑘_𝑖\) 总结了 $ 𝑢/𝑖$ 的 \(𝑘-hop\)​ 邻域内的信息。 在图 G 上，预测分数计算如下：

\[ \hat y_{u,i}=f(u,i)=<e_u^*,e_i^*> \space \space \space \space \space \space \space \space \space \space \space \space \space （3） \]

• 其中 \(𝑒^∗_𝑢\) 和 $ 𝑒^∗_𝑖$ 表示 $𝐾 $ 卷积层之后的高阶特征。 受 ResNet的启发，许多研究表明，使用跳跃连接来组合 GCN 层可以有效地解决过度平滑问题。 在一个常见的范式中，组合运算符用于从历史表示 \([𝑒^0_𝑢、𝑒^1_𝑢、···、𝑒^𝐾_𝑢 ]、[𝑒^0_𝑖、𝑒^1_ 𝑖、···、𝑒^𝐾_𝑖 ]\)​ 和 Eq.( 3) 可扩展为：

\[ e^∗_𝑢 = 𝐶𝑜𝑚𝑏 (e^0_𝑢, e^1_𝑢, ..., e^𝐾_𝑢 ), e^∗_𝑖 = 𝐶𝑜𝑚𝑏 (e^0_𝑖 , e^1_𝑖 , ..., e6𝐾_𝑖 ) ∈ R^{(𝐾+1)d} \space \space \space \space \space \space \space \space \space \space \space \space \space （4） \]

其中 \(𝐶𝑜𝑚𝑏\) 是 $ 𝑢 $ 和 \(𝑖\) 的 \(0\) 到 \(𝐾\) 顺序特征的任意组合。

• 在文献中，\(𝑢/𝑖\) 的高阶特征通常由两个树状结构计算，它们以 \(𝑢/𝑖\) 为根，由 \(𝐾\) 堆叠图卷积层组成，如图1a所示。 具体来说，对于两棵树中的任何父节点 𝑝，其子集 \(N_𝑝\) 是从 \(𝑝\) 在 G 中的直接邻居采样来的，并且父节点 𝑝 的 𝑘+1 阶特征是从他的子节点的 \(k\)​ 阶特征聚合过来的。

\[ e^{𝑘 +1}_𝑝 = 𝐴𝑔𝑔(e^𝑘_𝑐 : 𝑐 ∈ N𝑝 ), 𝑘 ∈ \{0, ..., 𝐾 - 1\} \space \space \space \space \space \space \space \space \space \space \space \space \space （5） \]

其中 \(𝐴𝑔𝑔\) 是一个聚合器函数，它结合了孩子的特征。 该卷积操作沿树从下到上迭代使用，产生 $ e^∗_𝑢$ 和 $ e^∗_𝑖$ 用于最终偏好预测。

3.3 IA-GCN模型

3.3.1 什么是交互？

• 对于任意两个不同的 item \(i \not = j\) , 用于预测 \(\hat y_{u,i}\) 和 \(\hat y_{u,j}\) 的嵌入表示 \(e_u^*\) 是一样的；
• 对于任意两个不同的 user$ u \not = v$ , 用于预测 \(\hat y_{u,i}\) 和 \(\hat y_{v,i}\) 的嵌入表示 \(e_i^*\) 是一样的；

意思是：对于不同的 item，按照原来的方法，用于预测 \(\hat y_{u,i}\) 和 \(\hat y_{u,j}\) 的嵌入表示 \(e_u^*\) 是一样的，现在想让\(e_u^*\) 是不一样的，对 i 更喜欢就会在预测 \(\hat y_{u,i}\) 的时候把 \(e_u^*\) 权重赋高。

为了解决这个限制，IA-GCN 在两棵树之间构建了显式交互：

• 目标用户 𝑢 指导项目(item)树中的聚合，即强调类似于 𝑢 的子项；
• 目标项目 𝑖 指导用户(user)树中的聚合，即为类似于 𝑖 的子项分配更高重要性。

这种交互式指南使 IA-GCN 能够通过每个图卷积关注特定于目标的信息。 因此，得到的目标 𝑢/𝑖 的高阶特征不是固定的，而是以目标用户-项目对中对应的 𝑖/𝑢 为条件：\(𝑒^∗_𝑢 |𝑖\) 和 \(𝑒^∗_𝑖 |𝑢\)。（即用于预测 \(\hat y_{u,i}\) 和 \(\hat y_{u,j}\) 的嵌入表示 \(e_u^*\) 现在是不一样的了，用\(𝑒^∗_𝑢 |𝑖\) 来预测 \(\hat y_{u,i}\)，用\(𝑒^∗_𝑢|j\)  来预测 \(\hat y_{u,j}\))

那么如何衡量要聚合的子节点与其向导（即另一棵树的根）之间的相似性?

3.3.2 交互指导

​ 考虑一个图卷积运算，它在节点 𝑔 的指导下，通过聚合其子节点 \(∀𝑐 ∈ N𝑝\) 的特征来计算父节点 𝑝 的高阶特征。

​ 使用交互式引导策略，有以下两种情况：

• \(𝑔 = 𝑖\)，并且 \(𝑐 ∈ N_u\) ，即目标 $item $指导 $user $树中的邻域聚合。 如图1b①所示。
• \(𝑔 = 𝑢\)，且 $ 𝑐 ∈ N_𝑖 $，即目标 $user $ 引导 $item $树中的邻域聚合。 如图1b②所示。

具体来说，当聚合到 𝑝 (父节点) 时，𝑐 的重要性是根据 𝑐 与引导 𝑔 的相似性/相关性来分配的。

该策略的有如下几个注意事项：

• 首先，𝑐 和 𝑔 的高阶特征虽然可用，但可能由于邻域传播而产生噪声。 所以只从 𝑐 和 𝑔 的 0 阶特征计算重要性分数。

• 其次，𝑐 和 𝑔 的嵌入向量的简单内积对于计算注意力系数应该是可行的。 当 𝑐 和 𝑔 是同构节点时，它用作相似度度量。 当它们是异质的时，它量化了用户-项目对之间的相关性。

• 第三，更多的孩子，即更大的 \(|N𝑝|\)，并不一定表明 \(𝑝\) 更重要。 所以 \(𝑝\) 聚合的高阶特征的规模不应该随着\(|N𝑝|\)的增加而增加。 因此，我们将控制 $∀𝑐 ∈ N𝑝 $ 上所有相似性的总规模。

• 最后，我们将由 𝑔 引导的孩子 𝑐 对 𝑝 的重要性公式化为:

\[ 𝛼_{𝑝, 𝑐}| 𝑔 =\frac {exp (<e^0_g, e_c> / 𝜏) }{\sum_{𝑐'∈N_p} exp(<e^0_g, e_{c′}> / 𝜏)} \space \space \space \space \space \space \space \space \space \space \space \space \space （6） \]

其中 \(𝜏\) 是温度参数。等式（6）中的 softmax 层为确保 \(\sum_{𝑐 ∈N_p}𝛼_{𝑝,𝑐} |𝑔 = 1\)。

请注意，IA-GCN 中的这种聚合重要性与 GCN 中现有的注意机制（例如 GAT 根本不同。 我们的 \(𝛼_{𝑝,𝑐}|𝑔\) 取决于𝑐 与𝑔 的相似性，即来自另一棵树的交互式引导。 而在现有的注意力中，\(𝛼_{𝑝,𝑐}\) 取决于 𝑐 与 𝑝 的相似性。 由于使用的知识仍然仅限于𝑐自己的单棵树，现有算法无法提取交互特征。

3.3.3 交互卷积

​ 在前面的部分中，关注如何在聚合器中分配重要性，现在我们深入研究式（5）中聚合器的设计。

​ 在文献中，早期的 GCN 工作大多属于繁重的流程：线性变换、加权和池化和非线性激活 。 虽然最近的研究强调了这样一个事实，即轻型聚合器（例如加权和池）通常可以实现最先进的性能。 以何向南老师的 LightGCN 模型为例。

​ 当聚合 $𝑐 ∈ N_𝑝 $到 \(𝑝\)​ 时，他们使用:

\[e^{𝑘 +1}_𝑝= \sum_{𝑐 ∈N_𝑝} \frac 1 { \sqrt{{|N_𝑝|}{|N_𝑐|}}}e^𝑘_𝑐 \space \space \space \space \space \space \space \space \space \space \space \space \space （7） \]

​ 其中它们的聚合权重是基于𝑐和𝑝自己的树中的信息的简单归一化。

​ 由于 IA-GCN 的重点是在两棵树之间引入交互式指导，我们建议遵循简单且经过验证的有效加权和池聚合器。 使用建议的交互式指导，我们的卷积操作被表述为:

\[e^{𝑘 +1}_𝑝|𝑔 = \sum_{𝑐∈N_𝑝}\space 𝛼_{𝑝,𝑐}|𝑔\space e^𝑘_𝑐 ,\space \space \space \space \space \space \space \space \space \space \space \space \space （8） \]

其中 $𝛼_{𝑝,𝑐}|𝑔 $是交互权重，在等式（6）中定义

请注意，IA-GCN 是一个易于插入的模块，理论上可以应用于任何基于 GCN 的推荐方法。 通过将我们的交互权重相乘，许多现有算法将受益于学习到的用户-项目交互知识。

3.3.4 层组合和模型预测

在介绍了消息传递的方式之后，我们通过公式（8）中定义的 𝐴𝑔𝑔 运算符从原始嵌入 𝑒0 开始聚合 𝑘 + 1 阶特征。 然后应用等式（4）中提到的组合算子从顺序层收集有影响的信息。 这样的𝐶𝑜𝑚𝑏操作可以重新表述如下：

\[e^∗_𝑝|𝑔 = 𝐶𝑜𝑚𝑏 (𝑒^0_𝑝|𝑔,\space 𝑒^1_𝑝|𝑔, · · · ,\space 𝑒^𝐾_𝑝|𝑔) \space \space \space \space \space \space \space \space \space \space \space \space \space （9） \]

具体来说，我们工作中的𝐶𝑜𝑚𝑏可以概括为：

\[e^∗_p|g =\sum_{k=0}^K\space 𝛽_𝑘\space 𝑒^𝑘_𝑝|𝑔 \\ s.t. 𝛽_𝑘 ≥ 0\quad \& \space \sum_{k=0}^K𝛽_𝑘 = 1 \space \space \space \space \space \space \space \space \space \space \space \space \space （10） \]

\(𝛽_𝑘\)表示从k 阶特征收集信息的比率/重要性。 \(𝛽_𝑘\)​不仅可以基于专家知识调整超参数，还可以与图卷积层共同学习变量。 与等式（2）一样，我们考虑到交互式引导的预测如下：

\[ \hat y_{𝑢, 𝑖} = 𝑓 (𝑢, 𝑖) = <e^*_𝑢 | 𝑖, e^*_𝑖 | 𝑢>\space \space \space \space \space \space \space \space \space \space \space \space \space （11） \]

它从早期阶段对目标用户和目标项目之间的交互进行建模，通过每个卷积操作保留宝贵的目标特定信息，并在最后对交互概率进行预测。

4. 实验结果