张量分解与应用-学习笔记[03]

4 压缩与Tucker分解法

4.0 Tucker分解法定义

• Tucker分解法可以被视作一种高阶PCA. 它将张量分解为核心张量(core tensor)在每个mode上与矩阵的乘积. 因此, 对三维张量\(\mathcal{X}\in\mathbb{R}^{I \times J \times K}\)来说, 我们有如下分解:

\[(4.1) \mathcal{X} \approx \mathcal{G}\times_1 \mathrm{A} \times_2 \mathrm{B} \times_3 \mathrm{C} = \sum_{p=1}^P\sum_{q=1}^Q\sum_{r=1}^R g_{pqr} \: \mathrm{a}_p\circ \mathrm{b}_q\circ \mathrm{c}_r = [\![\mathcal{G}\,;A,B,C]\!]. \]

• 其中, \(\mathrm{A}\in \mathbb{R}^{I\times P}\), \(\mathrm{B}\in\mathbb{R}^{J\times Q}\), 和 \(\mathrm{C} \in \mathbb{R}^{K\times R}\)被称之为因子矩阵, 他们通常是正交的(orthogonal). 他们通常可以被作每个mode下的主成分principal components. 其中, 张量\(\mathcal{G} \in \mathbb{R}^{P \times Q \times R}\) 被称之为核心张量(core tensor). 他的每个数字元素代表了不同成分之间的互动程度.
  

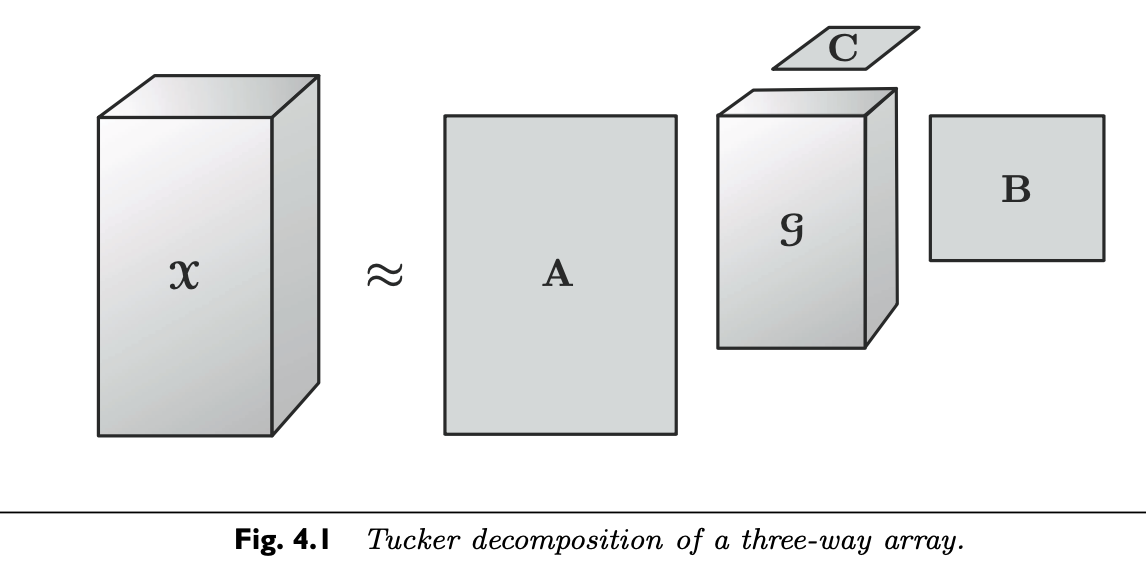
• 对每个元素来说, Tucker分解法可以写作:

\[x_{ijk} \approx \sum_{p=1}^P \sum_{q=1}^Q \sum_{r=1}^R g_{pqr}a_{ip}b_{jq}c_{kr} \quad \text{for} \quad i = 1,\dots,I, j =1,\dots,J, k=1,\dots,K. \]

• \(P,Q\)和\(R\)为对应的因子矩阵\(A,B\)和\(C\)的成分数(例如列向量的数目). 如果\(P,Q,R\)小于\(I,J,K\), 我们可以将核心张量\(\mathcal{G}\)视作\(\mathcal{X}\)的一个压缩版本. 在某些情况下, 压缩版本所需的空间远远小于原始张量.

• 大多数的拟合算法假设因子矩阵的列向量是单位正交(orthnonormal)的, 但其实这并不是必要的. 事实上, CP分解法可以被视作为Tucker分解法的一个特例: 也就是当满足核心张量为超对角张量并\(P=Q=R\).

• 矩阵化后的形式为:

\[\mathrm{X}_{(1)} \approx \mathrm{A}\mathrm{G}_{(1)}(\mathrm{C}\otimes \mathrm{B})^\mathsf{T}, \]

\[\mathrm{X}_{(2)} \approx \mathrm{B}\mathrm{G}_{(1)}(\mathrm{C}\otimes \mathrm{A})^\mathsf{T}, \]

\[\mathrm{X}_{(3)} \approx \mathrm{C}\mathrm{G}_{(1)}(\mathrm{B}\otimes \mathrm{A})^\mathsf{T}. \]

• 上述公式以3维张量为例, 而这不妨碍其概念扩展到N维张量:

\[\mathcal{X} = \mathcal{G} \times_1 \mathrm{A}^{(1)} \times_2 \mathrm{A}^{(2)}\dots \times_N \mathrm{A}^{(N)} = [\![\mathcal{G}; \mathrm{A}^{(1)}, \mathrm{A}^{(2)}, \dots , \mathrm{A}^{(N)}]\!] \]

• 对每个元素来说

\[x_{i_1i_2\dots i_N}=\sum_{r_1=1}^{R_1} \sum_{r_2 = 1}^{R_2} \dots \sum_{r_N=1}^{R_N}g_{r_1r_2\dots r_N}a^{(1)}_{i_1r_1}a^{(2)}_{i_2r_2}\dots a_{i_N r_N}^{(N)} \\ \quad \text{for} \quad i_n =1,\dots,I_n, n=1,\dots,N. \]

• 矩阵化版本可写为

\[\mathrm{X}_{(n)} = \mathrm{A}^{(n)}\mathrm{G}_{(n)}(\mathrm{A}^{(N)}\otimes \dots \otimes \mathrm{A}^{(n+1)}\otimes \mathrm{A}^{(n-1)}\otimes \dots \otimes \mathrm{A}^{(1)})^\mathsf{T}. \]

• 另有两个Tucker分解法的变种值得特别注意. 首先是Tucker2分解法. 顾名思义, 他只使用某2个矩阵来分解, 第三个矩阵为单位矩阵, 故一个三阶张量的Tucker2分解可以写为以下形式:

\[\mathcal{X} = \mathcal{G}\times_1 \mathrm{A} \times_2 \mathrm{B} = [\![\mathcal{G}\,;\mathrm{A,B,I}]\!]. \]

• 这和原始的Tucker分解其实没什么不同, 唯独\(\mathcal{G}\in\mathbb{R}^{P \times Q \times R}\)且 \(R=K\) 并 \(\mathrm{C=I}\) (\(K\times K\)的单位矩阵). 类似的, Tucker1分解法只利用某一个矩阵来分解并将剩余矩阵设为单位矩阵. 例如, 如果设第二和第三因子矩阵为单位矩阵, 我们可以得到:

\[\mathcal{X} = \mathcal{G} \times_1 \mathrm{A} = [\![\mathcal{G}\,;\mathrm{A,I,I}]\!]. \]

• 这等价于一个标准的2维PCA(主成分分析). 因为

\[\mathrm{X}_{(1)} = \mathrm{A}\mathrm{G}_{(1)}. \]

• 这些概念很轻松便可延伸至N维张量: 我们可以设任何因子矩阵们的子集为单位矩阵.

• 很显然, 张量分解有着许多的选择, 有时候会给我们根据特定任务选择模型时带来麻烦. 想要了解3维下如何选择模型的, 可以参考此论文.

4.1. The n-Rank

• 令\(\mathcal{X}\)为一个尺寸为\(I_1\times I_2 \times \dots \times I_N\)的N阶张量. 那么, 他的n-rank, 写作\(\text{rank}_n(\mathcal{X})\)是\(\mathrm{X}_{(n)}\)的列秩(column rank). 换句话说, n-rank是mode-n fiber所生成的(span)向量空间的维度.如果我们令\(R_n=\text{rank}_n(\mathcal{X})\,\text{ for }\, n=1,\dots,N\), 那么我们可以说\(\mathcal{X}\)是一个\(\text{rank}-(R_1,R_2,\dots,R_N)\)张量.

• n-rank切记不能与秩(rank), 也就是最小的秩1成分数目, 所混淆.

• 显然, \(R_n \leq I_n \text{ for all }n=1,\dots,N.\)

• 对于一个给定的张量\(\mathcal{X}\), 我们可以很轻易地找到一个秩为 \(\big( R_1,R_2,\dots,R_N \text{ where }R_n = rank_n(\mathcal{X})\big)\)的精确( exact ) Tucker分解. 但如果我们计算的Tucker分解的秩低于这组值, 也就是对某些n来说\(R_n < \text{rank}_n(\mathcal{X})\) 那么, 我们将必然无法获得精确的结果并且其计算会变得更为困难. 下图展示了truncated Tucker Decomposition (并不一定要从一个精确Tucker分解中舍项得来). 该分解将不能精确地还原\(\mathcal{X}\)

4.2. Tucker分解法的计算

• 计算Tucker分解的第一个可行的方法来自于前文所述的Tucker1算法, 即, 舍去一个矩阵来最大程度的捕捉其mode-n fiber的分布变化(variation). 由于后人的研究和分析, 此法后来又被称之为higher-order SVD(HOSVD). 研究者指出, HOSVD是一个可信的矩阵SVD的一般化理论, 并且讨论了很多如何更有效率的计算\(\mathrm{X}_{(n)}\)的前排奇异向量的方法. 当对某些n, \(R_n<\text{rank}_n(\mathcal{X})\)的时候, 我们称之为truncated HOSVD. 事实上, HOSVD的核心张量是全正交(all-orthogonal)的, 这与分解时的舍位(truncate)有关. 详情请见此论文

• truncatd HOSVD在最小化估计错误的范数这个角度上来说并不是最优的, 但给迭代交替最小方差法(iterative ALS algorithm)提供了一个不错的起点. 1980年, 计算三维张量的Tucker分解的ALS法TUCKALS3诞生了. 然后该法被延伸至对n维张量也有效. 同时, 一种更为有效的计算因子矩阵的方法被运用: 简单地说, 只去计算\(\mathrm{X}_{(n)}\)的主奇异向量(dominant singular vectors). 并且运用SVD来代替特征值分解(eigenvalue decomposition)或者只计算其主子空间(dominant subspace)的单位正交基底向量(orthonomal basis)即可. 这种崭新的提高效率的算法被称之为更高维正交递归(higher-order orthogonal iteration HOOI). 见下图4.4.

• 设\(\mathcal{X}\)是一个\(I_1 \times I_2 \times \dots \times I_N\)尺寸的张量, 那么我们渴望解决的优化问题可以被写作:

\[\begin{aligned} (4.3) \quad \min_{\mathcal{G}, \mathrm{A}^{(1)},\dots,\mathrm{A^{(N)}}} &\Big|\Big| \mathcal{X} - [\![\mathcal{G}\,;\mathrm{A}^{(1)},\mathrm{A}^{(2)},\dots,\mathrm{A}^{(N)}]\!]\Big|\Big| \\ &\mathcal{G}\in\mathbb{R}^{R_1\times R_2 \times \dots \times R_N},\,\mathrm{A}^{(n)}\in \mathbb{R}^{I_n \times R_n}, \text{columnwise orthogonal for all n} \end{aligned} \]

• 上述目标函数改写为矩阵形式后如下:

\[\big|\big| \text{vec}(\mathcal{X}) - (\mathrm{A}^{(N)}\otimes\mathrm{A}^{(N-1)}\otimes \dots \otimes \mathrm{A}^{(1)})\text{vec}(\mathcal{G}) \big|\big| \]

• 显然, 核心张量\(\mathcal{G}\)必须满足

\[\mathcal{G} = \mathcal{X} \times_1 \mathrm{A}^{(a)\mathsf{T}} \times_2 \mathrm{A}^{(2)\mathsf{T}} \dots \times_N \mathrm{A}^{(N)\mathsf{T}}. \]

• 那么我们就能把上述目标函数(的平方)写为:

\[\begin{aligned} \Big|\Big|\mathcal{X} - &[\![\mathcal{G}\,; \mathrm{A}^{(1)}, \mathrm{(2)},\dots,\mathrm{A}^{(N)}] \!]\Big|\Big|^2 \\&= ||\mathcal{X}{||}^2 - 2 \langle \mathcal{X}, [\![\mathcal{G}\,;\mathrm{A}^{(1)},\mathrm{A}^{(2)},\,\dots,\mathrm{A}^{(N)}]\!]\rangle + ||\mathcal{G}\,;\mathrm{A}^{(1)},\mathrm{A}^{(2)},\dots,\mathrm{A}^{(N)}{||}^2\\ &= ||\mathcal{X}{||}^2 - 2\langle \mathcal{X} \times_1 \mathrm{A}^{(1)\mathsf{T}}\dots \times_N \mathrm{A}^{(N)\mathsf{T}},\mathcal{G}\rangle + ||\mathcal{G}{||}^2\\ &= ||\mathcal{X}{||}^2 - 2\langle \mathcal{G},\,\mathcal{G}\rangle + ||\mathcal{G}{||}^2\\ &= ||\mathcal{X}{||}^2 - ||\mathcal{G}{||}^2\\ &= ||\mathcal{X}{||}^2 - ||\mathcal{X}\times_1 \mathrm{A}^{(1)\mathsf{T}} \times_2 \dots \times_N \mathrm{A}^{(N)\mathsf{T}}{||}^2. \end{aligned} \]

• 此变形的细节在多篇论文中提及,如此篇论文,及这篇论文.

• 我们仍然可以使用ALS来解(4.3)的目标函数, 由于\(||\mathcal{X}||\)是个常数, (4.3)可以被重新定义为一系列包含如下最大化问题的子问题集, 其中每个n对应了第n个成分矩阵:

\[(4.4)\quad\quad\max_{\mathrm{A}^{(n)}}\Big|\Big|\mathcal{X}\times_1 \mathrm{A}^{(1)\mathsf{T}} \times_2 \mathrm{A}^{(2)\mathsf{T}}\dots \times_N\mathrm{A}^{(N)\mathsf{T}}\Big|\Big|\\ \text{subject to $\mathrm{A}^{(n)}\in \mathbb{R}^{I_n\times R_n}$ and columnwise orthogonal.} \]

• 目标函数(4.4)也可以被写作矩阵形式:

\[\Big|\Big|\mathrm{A}^{(n)\mathsf{T}}\mathrm{W}\Big|\Big| \text{ with } \mathrm{W} = \mathrm{X}_{(n)}(\mathrm{A}^{(N)}\otimes\dots\otimes\mathrm{A}^{(n+1)}\otimes\mathrm{A}^{(n-1)}\otimes\dots\otimes\mathrm{A}^{(1)}). \]

• 其解可以被SVD所确定:只需将\(A^{(n)}\)定义为W的前\(R_n\)个奇异向量即可. 这种方法会收敛至一个解使得目标函数不再下降, 但并不确保收敛至一个全局最优解甚至是一个驻点.

• 最近, Newton-Grassmann优化法也被考虑进计算Tucker分解法之中. 他使得解可以收敛至一个驻点, 且速度更快(即使每次迭代的计算成本变高了). 详情请参考
  此论文

• 此论文着重讲述了如何选择Tucker分解法的rank, 和我们CP分解法讨论时类似, 他通过计算一个HOSVD来做出选择.

4.3. 唯一性的缺乏及克服它的方法

• Tucker分解法的结果并不是唯一的. 考察一个普通的3维分解(4.1, 见本文开头), 令\(\mathrm{U}\in\mathbb{R}^{P\times P}\), \(\mathrm{V}\in \mathbb{R}^{Q\times Q}\)和\(\mathrm{W}\in\mathbb{R}^{R\times R}\)为非奇异矩阵. 那么:

\[[\![\mathcal{G}\,;\mathrm{A},\mathrm{B},\mathrm{C}]\!] = [\![\mathcal{G} \times_1 \mathrm{U} \times_2 \mathrm{V} \times_3 \mathrm{W}\,;\mathrm{AU}^{-1}, \mathrm{BV}^{-1}, \mathrm{CW}^{-1}]\!]. \]

• 换句话说, 我们可以通过将因子矩阵乘以相反的修改方式来抵消修改核心张量\(\mathcal{G}\)的影响,从而使得我们可以不影响拟合的情况下随意修改核心张量.

• 这种自由度延伸出了一种新的分支: 选择一种修正法使得核心矩阵的大部分元素为0, 通过降低不同成分之间的互相影响来尽可能提高唯一性. 核心矩阵的超对角被证明是不可能的, 但尽可能多的使得元素为0或接近于0是可能的. 一种方式是通过简化核心来使得目标函数最小化; 另一种方式是用Jacob及类型的算法最大化对角上的值; 最后, 我们提到过HOSVD的解为一个全正交的核, 这种特殊的类型也许会被证实有用.

Tucker分解法的介绍就到此结束了. 本文仍然缺少一些例子与引用论文的原理讲述, 将在日后补足.
下一章将是最后一章: 多种其他分解法的介绍, 欢迎关注!