堆结构及堆排序详解

一、物理结构和概念结构　

　　学习堆必须明确，堆有两个结构，一个是真实存在的物理结构，一个是有助于理解的概念结构。

　　1. 堆一般由数组实现，但是我们平时在理解堆的时候，会把他构建成一个完全二叉树结构。堆分为大根堆和小根堆：大根堆，就是这颗树里的每一个结点都是以它为根结点的树中的最大值；小根堆则与之相反。

　　

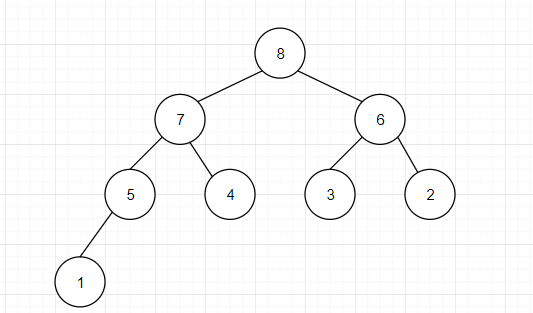
 　　（注意一定要是完全二叉树）

 　　2. 物理结构：从 0 开始的数组。

 　　怎么将数组和二叉树联系起来呢？

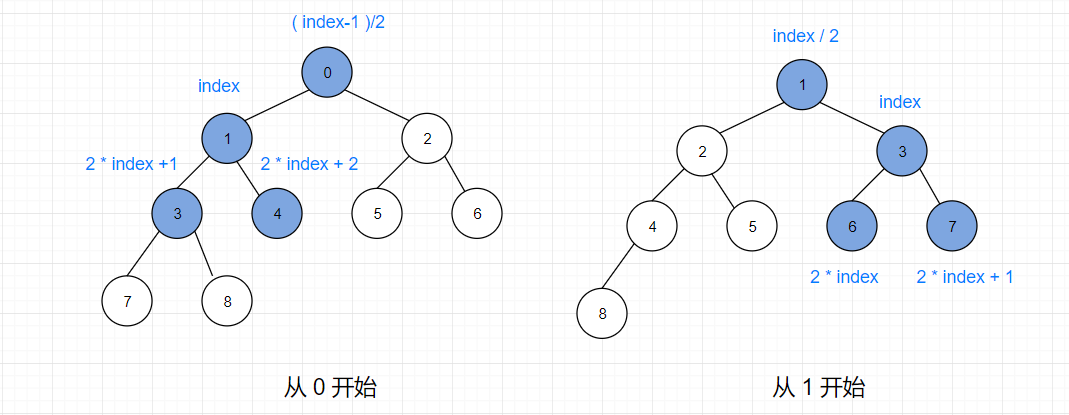
　　当一个结点在数组中的下标为 index，那么这个结点对应的父节点的下标为 ( index-1 ) / 2，左孩子的下标为  2 * index +1 ，右孩子的下标为  2 * index +2 。

　　上面是以 0 开始的数组中各结点对应的关系，数组也可以以 1 开始，此时父节点下标为  index / 2，左孩子下标为 2 * index，右孩子下标为 2 * index + 1。

　　有一个物理数组下标从 0 - 8

　　

 　　树结构为：

　　

 二、heapInsert

　　当数组中 0 ~ index -1 的位置已经是大根堆，现在添加一个元素到下标为 index ，需要怎么做才能继续保持大根堆的结构呢？

　　1. 将新增元素index 与 父节点 ( index-1 ) / 2  比较，若比父节点大，则与父节点交换位置；

　　2. 交换位置后，新增元素下标变为 父节点的下标，再与现在这个节点的父节点比较，周而复始；

　　3. 直至 新增节点不再比父节点大或者已经到达了根结点，则新增节点的插入位置确定

　　例子：现在有一个已经在 0 ~ 7 形成大根堆的数组 [ 24, 18, 20, 10, 9, 17, 8, 5 ] ，在下标为 8 的位置插入元素 22.

　　

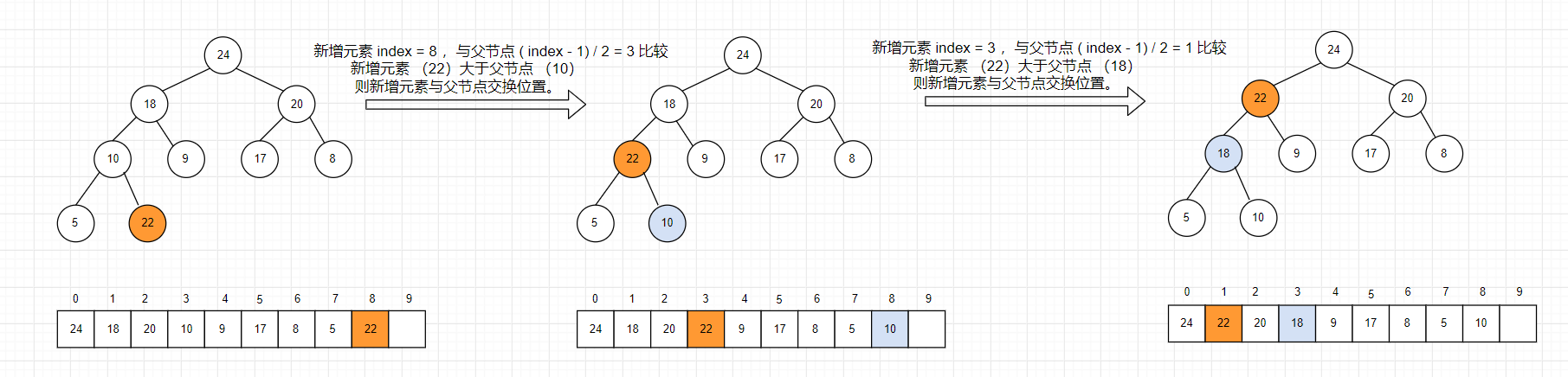
 　　JAVA 实现：

    public static void heapInsert(int[] arr, int index) {
        // 停止条件1：新增结点不再比父节点大
        // 停止条件2：已经到达了整棵树的 根结点 0 ，当 index = 0，（ 0-1）/2 =0，所以arr[index] 和 arr[(index - 1) / 2] 相等
        while (arr[index] > arr[(index - 1) / 2]) {
            swap(arr, index, (index - 1) / 2);
            index = (index - 1) / 2;
        }
    }

    public static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

 三、heapify

　　当将最大值 pop 出去之后，需要对这个堆进行调整，最常用的就是，将堆结构中最后一个的数提到 0 下标，然后将这个数从 0 开始下沉。

　　某个数在 index 位置，看是否可以往下沉。这就是 heapify。

　　当index 还有孩子节点时，比较左右两个节点的大小，选取节点值较大的一个，与index进行比较 ，若 子节点的值较大，父节点下沉，较大孩子上来。直至比孩子节点大或者没有孩子节点。

　　

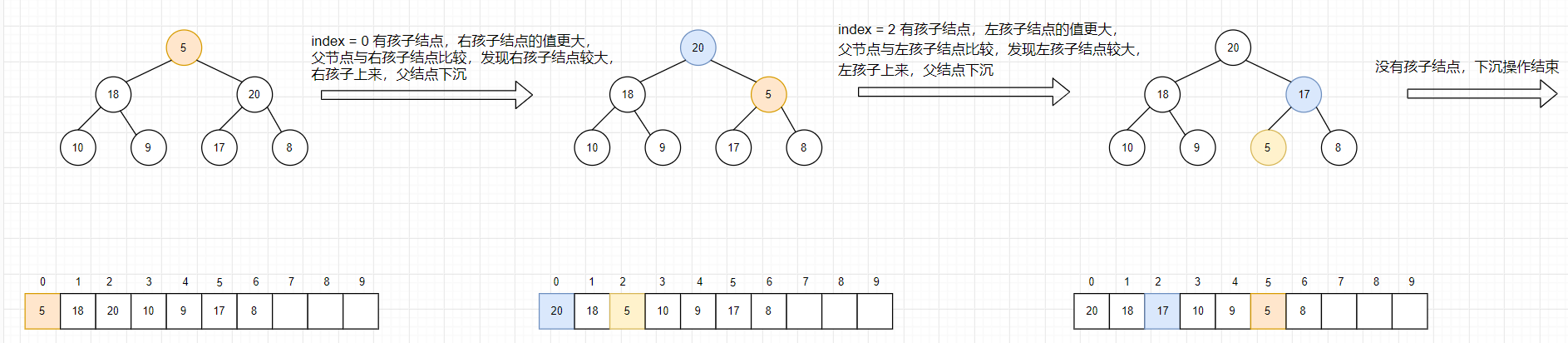
 　　JAVA 实现：

    public static void heapify(int[] arr, int index, int heapSize) {
        int left = index * 2 + 1;// 左孩子的下标
        while (left < heapSize) {// 下方还有孩子的时候
            // 两个孩子中，谁的值大，把下标给 largest变量
            int largest = (left + 1 < heapSize) && (arr[left + 1] > arr[left]) ? left + 1 : left;
            // 父与较大的孩子之间，谁的值大，吧下标给 largest
            largest = arr[largest] > arr[index] ? largest : index;
            if (index == largest) {
                break;
            }
            swap(arr, index, largest);
            index = largest;
            left = index * 2 + 1;
        }
    }

 

四、堆排序（非递减）

　　堆排序一共分为两步，第一步是将数组构建成一个大根堆，第二步将堆结构中的根结点，也就是最大值，移到堆的最后，然后将这个结点从堆中移除。

　　1. 将数组构建成一个大根堆。有两种方法，但是这两种方法会有不同的事件复杂度。

　　（1）使用 heapInsert。index 从 1 开始（因为从 0 开始的话，只有一个元素，没有必要），直至最后一个元素 arr.length -1 ，每个元素都使用 heapInsert 的方式，逐个形成 [ 0,..., index] 的大根堆.

for (int index = 1; index < arr.length; index++) {// O(N)
    heapInsert(arr, index);// O(logN)
}

　　每个元素最多向上进行 log2(N)次比较和交换，一共有 N 各元素，所以需要 O(NlogN) 的事件复杂度。

　　这种方法比较适合逐个向数组中添加元素，但是此时排序，传进来的是整个数组，所以我们有一种可以将事件复杂度降低为 O(N) 的方式。

　　（2）使用 heapify。从最后一个元素开始，不断下沉，使得以这个元素为根结点的数形成堆结构。

　　

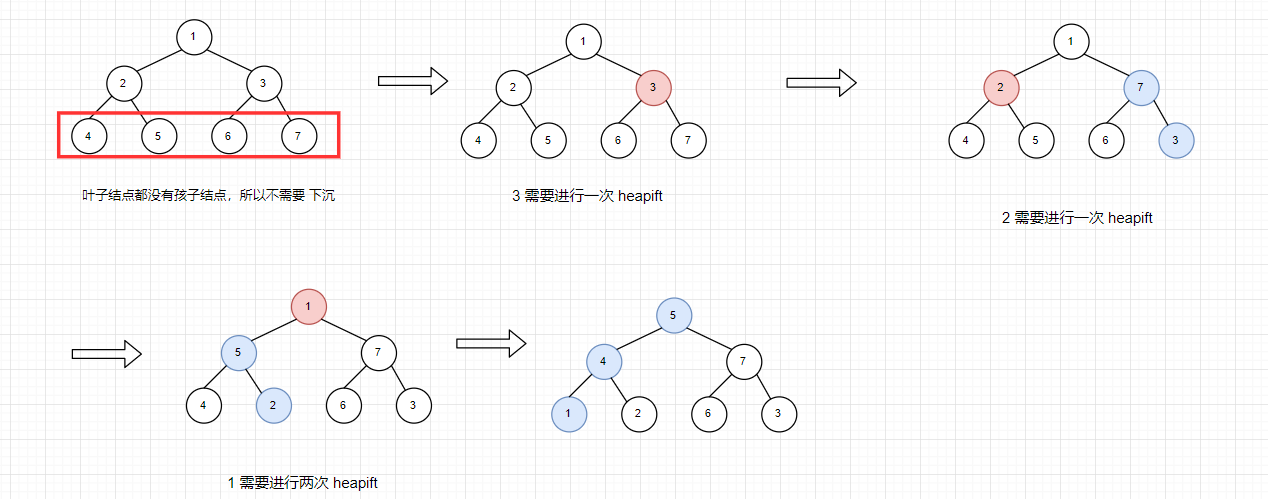
 　　为什么说事件复杂度为 O(N) 呢？

　　

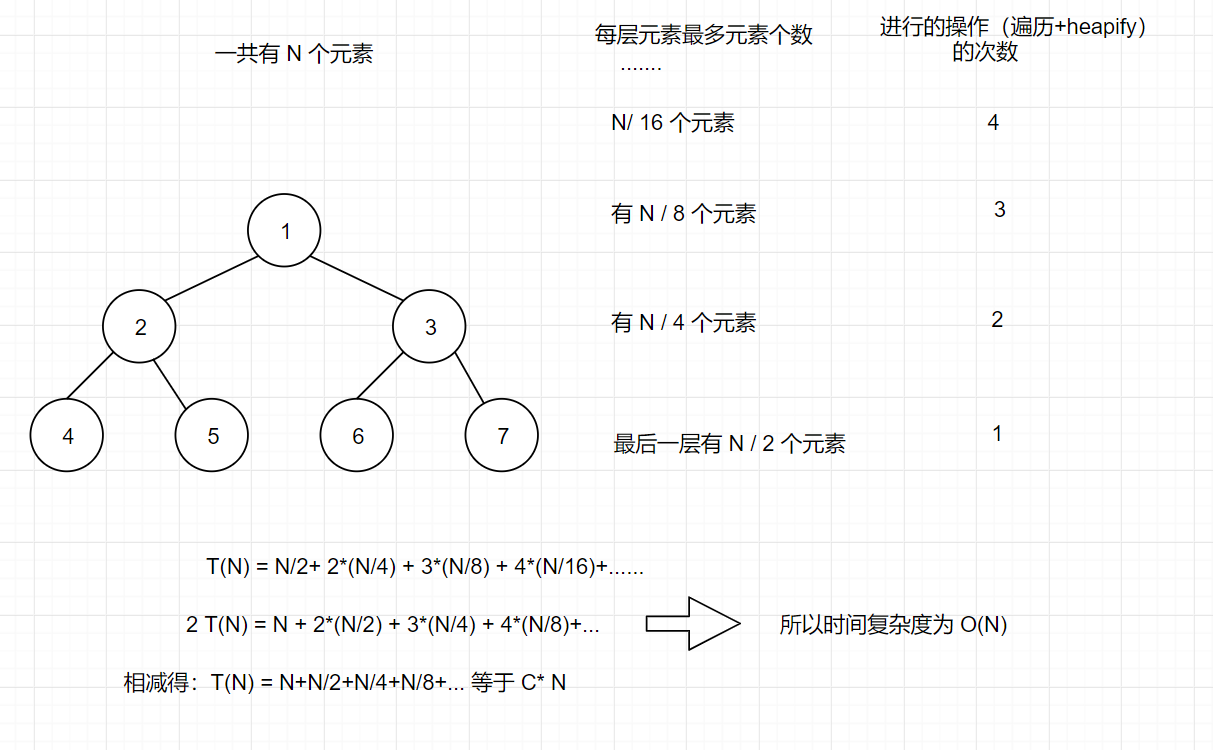
 　　Java 实现：

for (int index = arr.length - 1; index >= 0; index--) {
    heapify(arr, index, arr.length);
}

 

　　2. 将堆结构中的根结点，也就是最大值，移到堆的最后，然后将这个结点从堆中移除。

　　将堆中最大值逐个放在 arr.length-1,arr.length-2,...,1 的位置。使用 heapSize 记录堆中元素得个数，将堆中最大值往后，其实就是和堆中最后一个元素（下标为 heapSIze-1）交换位置，此时最后一个元素到达根结点 0 。交换完成后 heapSize--，意味着这个元素已经排序完成并将它从堆中移除，再调用 heapify 将提到根结点 0 得元素下沉。事件复杂度为 O(logN)

　　int heapSize = arr.length;// 记录堆中元素的个数，如果一个数排序完成（放在堆数组的最后），就将他从堆数组中除去(heapSize--);
 　swap(arr, 0, --heapSize);// 将堆中的最大值放在数组的最后，此时最大值排序完成，堆数组的个数减一
　　while (heapSize > 0) {// O(N)
        heapify(arr, 0, heapSize);// O(logN)
        swap(arr, 0, --heapSize);// O(1)
    }

　　形成堆结构，我们采用第二种方法，所以最后堆排序的代码为：

    // 堆排序
    public static void heapSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        // 形成大根堆：
        // O(N)
        for (int index = arr.length - 1; index >= 0; index--) {
            heapify(arr, index, arr.length);
        }

        // 将堆中最大值逐个放在 arr.length-1,arr.length-2,...,1 的位置
        // O(N*logN)
        int heapSize = arr.length;
        swap(arr, 0, --heapSize);
        while (heapSize > 0) {// O(N)
            heapify(arr, 0, heapSize);// O(logN)
            swap(arr, 0, --heapSize);// O(1)
        }
    }