线性回归——梯度下降

一、概述

　　线性回归是利用数理统计中的回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，在机器学习中属于监督学习。在数据分析等领域应用十分广泛。

　　很多情况下我们都用它进行预测，比如预测房屋价格。在这里用一个简单的例子来说明，假设有一组房屋数据，为了理解方便，假设决定价格的只有房屋到市中心的距离：

Distance(km)	Price(￥/m2)
5	100000
10	80000
15	60000
25	50000
30	30000

 

　　从上面自拟的数据可以看到，距离越小价格就会越大。那么问题来了，假如你有一套房，距离市中心大约有8km，你想要知道大概能卖多少钱？这个时候线性回归就起作用了。

将数据大概地绘制成如下的图，由此可见这套房大致上能卖92000￥

                                                                 

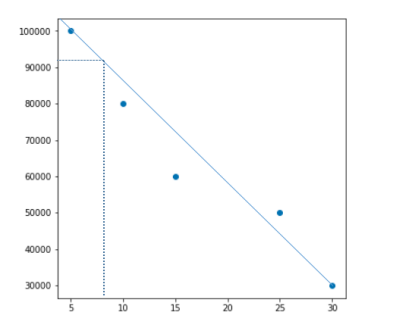
　　这就是线性回归，它可以用来预测值。在现实中，决定性的因素绝对不止一个，数据往往是多维的，那就会变得有些复杂了，这时候就需要通过算法来实现了。在学习算法之前，可以先过一下有关的数学知识。

二、数学基础

1、导数

　　导数这个概念在高中的时候就接触了，它的几何意义为函数y=f(x)在某一点处沿x轴正方向的变化率，通俗地讲，代表函数的斜率。

2、偏导数

             

　　偏导数的概念其实跟导数差不多，区别就在于偏导数一般是对于多元函数而言，y=f(x1,x2,…,xn)在某一点处沿某一坐标轴（x1,x2,…,xn）正方向的变化率。也就是说，函数对x1的偏导即为函数在x1方向上的变化率。

3、方向导数

 

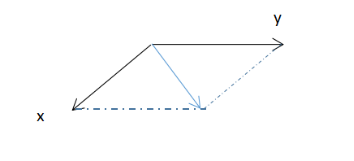
　　方向导数是建立偏导数的基础上的一个数学定义，偏导是指在正方向的变化率，而方向导数是指在其他特定方向上的变化率。以二元函数为例，假设已知x，y方向上的偏导，那么方向导数就可以是图中蓝色箭头方向上的数值（不要被图片迷惑了，它可以是其他任意方向上的数值，而且它是个标量）。

                                 

4、梯度

　　梯度是一个向量，即有方向有大小，它的方向是最大方向导数的方向，它的值是最大方向导数的值。就跟介绍方向导数的图那样，蓝色的矢量，代表的就是梯度。

 

三、算法介绍

　　在线性回归中，回归方程为：,通过这个方程得到的预测值往往与真实值y之间会存在误差。令误差为，则预测值与真实值之间的关系就可以表示为，我们希望求出来的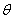使得误差最小。因此，我们假设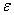服从均值为0，方差为的正态分布，根据正态分布的概率密度函数可得，其中==。

　　为了使得误差尽可能的小，根据上式，我们可以令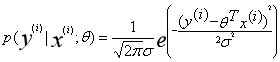，这个公式表示求使得预测值更接近于真实值的值的概率，因此我们希望它的值越大越好。接下来进行最大似然估计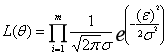：，相比于累加，这个公式累乘计算的难度会更大，所以不妨把它转换成对数形式，如下图所示：

 　                   　

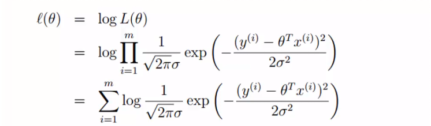
　　最后得到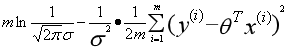： ，在这个式子中，起关键作用的式子是，我们称它为代价函数（Cost Function）。我们希望代价函数越小越好，因此我们需要求它的极小值，或者说局部最小值。假如只有一个，那么这个代价函数的图像可以这样表示：

 

 

　　可以看到，当曲线的斜率为0，即函数的导数值为0时，函数值最小。这只是对于一元函数而言，可事实上我们的数据是很多维度的，因此我们就需要通过梯度来得到我们需要的值。于是，梯度下降算法就出现了。

　　梯度下降算法是这样的：

　　repeat until convergence {

　　　　;

　　}

　　其中，称为速率因子，表示梯度下降的速度。对于这个算法，通俗点说，假设初始的时候某个点在曲面（曲线）上，它找到相对比较“陡峭”的方向，沿着这个方向“下坡”，直到最低点为止。在这里需要注意的一点是，的值不宜太小也不宜太大，太小会使得“下坡”的次数很多，影响效率；太大的话可能会错过最低点。通常我们可以通过斜率的值改变的值。