高速公路【贪心·区间选点】

• 题目描述
  一天，唐僧得到了一个消息，在遥远的西天有许多宝藏，他决定去寻找宝藏。
  在通往目的地的路途上要通过一片人迹罕至的空地，空地中央只有一些零星的村庄。为了节约时间，他决定在出发前让他的三个徒弟在这片空地边缘（即x轴）修一条笔直的高速路。 因为路途遥远，而且他们并不会瞬移，所以他们不得不经常下道，寻找一个村庄进行补给。
  唐僧的三个徒弟叫苦不迭，不想修太多的下道口。因此，他们决定聘请智慧的你，在高速路上设计出最少的出口，使得每个村庄到离他最近的一个出口的距离不超过D。
  注意：本题的距离指欧几里德距离，且距离值为浮点数。

• 输入格式
  多组数据，对于每组数据：
  第一行是高速路的长度 L（高速路从坐标原点开始）；
  第二行是最大距离 D；
  第三行是村庄的个数 N；
  接下来的 N 行，每行有两个整数 X,Y，表示这一个村庄的坐标.
  输入数据保证有解。

• 输出格式
  对于每组数据：
  一行，最少的出口个数。

• 样例输入

100
50
3
2 4
50 10
70 30

• 样例输出

1

思路解析

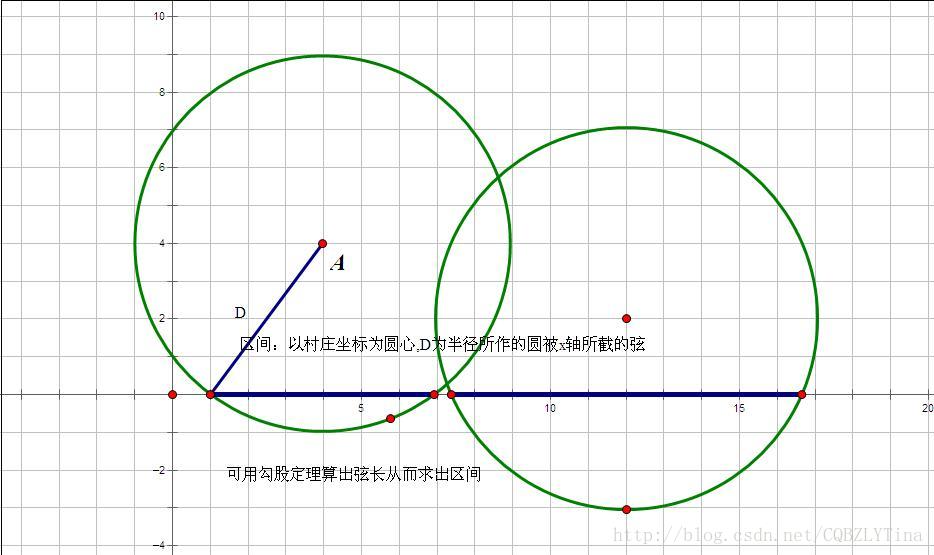
如图，我们可以求出出口应在的区间内。
然后，是不是觉得这道题特别熟悉呢？这道题就转化为了贪心算法中的区间选点问题。
这里简单描述一下，以右端点从左到右排序，然后每次选点选在区间的右端点，如果两个区间有重叠部分就可以共用一个出口。

程序实现

#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
#define MAXN 1000
struct node{
    int x,y;
    double l,r;
}a[MAXN+5];
int L,D,N;
bool cmp(node p,node q)
{
    return p.r<q.r;
}
int main()
{
    while(scanf("%d %d %d",&L,&D,&N)!=EOF)
    {
        for(int i=1;i<=N;i++)
        {
            scanf("%d %d",&a[i].x,&a[i].y);
            double temp=sqrt(D*D-a[i].y*a[i].y);
            a[i].l=a[i].x-temp>=0?a[i].x-temp:0;
            a[i].r=a[i].x+temp<=L?a[i].x+temp:L;//计算区间左右端点，用勾股定理
        }
        sort(a+1,a+N+1,cmp);//按右端点排序
        double x=-1;
        int ans=0;
        for(int i=1;i<=N;i++)//贪心
            if(a[i].l<=x) continue;
            else
            {
                ans++;
                x=a[i].r;
            }
        printf("%d\n",ans);
    }
}