【图论】拓扑排序&判环

定义

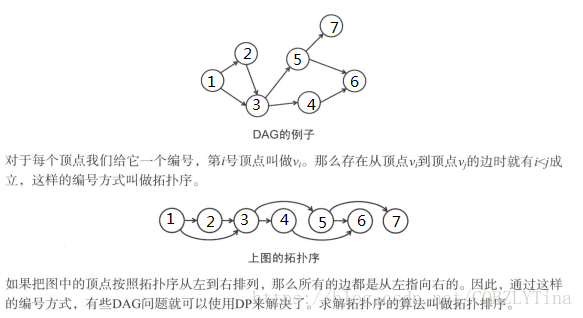
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。

实现步骤

1. 在有向图中选一个没有前驱的顶点并且输出
2. 删除所有和它有关的边
3. 重复上述两步，直至所有顶点输出，或者当前图中不存在无前驱的顶点。后者代表我们的有向图是有环的，因此，也可以通过拓扑排序来判断一个图是否有环。

/*
那个。。。我当初看这个结论的时候。。。自己画了个图。。。然后验证的时候。。。看漏了一个点的前驱。。。然后“勇敢”地质疑了（不存在） 请教了一下DaLao 然后。。。 感觉自己智商被碾压了。。。Orz
*/

无向图的判环

环上的点 度数>=2 (与环外的点有边时 度数>2)

1. 删除所有度<=1的顶点及相关的边，并将另外与这些边相关的其它点的度减1
2. 将度数变为1的点重复上步骤
3. 如果最后还有未删除顶点，则存在环，否则没有环

——————————分·界·线———————————

参考博客
https://blog.csdn.net/qq_35644234/article/details/60578189