【技巧-数学】反素数及其在OI中的应用
概念：对于任何正整数n，其约数个数记为f(n)，如果某个正整数n满足：对任意的正整数i(0< i< n)都有f(i)< f(n)，则称n为反素数。
emmm…，这个概念有点啰嗦，反素数其实就是区间里因子个数最多的那个数。
信竞中有如下应用：
- 求约数刚好等于n的最小的那个数
- 求区间里的最小反素数（[1,n]）
- 求区间里的最小反素数（[l,r]）
2和3其实也是有区别的，2可以加速，3只能暴力
求约数刚好等于n的最小的那个数
应用 Number With The Given Amount Of Divisors CodeForces - 27E
我们先来说一下第一个
首先，显而易见，我们想到的第一个想法就是大暴力，但是显而易见，它会T
然后，因数分解与质因数分解有着莫大的关系 每个数都能分解质因数（假设存在一个因数是合数，则这个合数还可以继续分解），若存在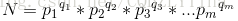
则N的因子个数为
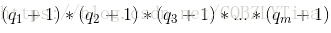
（因数个数定理）
证明也非常容易，其实就是质因子的组合，简单的乘法原理
0~q1个p1,0~q1个p2,0~q3个p3…一直到0~q4个p4相乘
但是这种做法的时间复杂度也很高
于是我们想到可不可以反过来做，枚举每一个质数以及它的个数，相乘直至到达区间的上限n，记录下因子的个数并不断更新答案。
既不浪费时间，也不会遗漏。
还可以继续优化。 我们看以下的例子：
- 6=2*3 10=2*5
6和10的质因数分解“模式”完全相同，所以它们的约数个数是相同的。但是由于3<5，所以6<10。 12=2^2*3 18=3^2*2
12和18的质因数分解“模式”完全相同，所以它们的约数个数是相同的。但是由于12的质因数分解中2的指数大于3的指数，18的质因数分解中3的指数大于2的指数，所以12<18。根据以上的举例，我们可以在枚举时进行一个优化，使得枚举到的数字中2的指数不小于3的指数，3的指数不小于5的指数……这样我们就能够得到质因数分解“模式”相同的最小数。
这个算法的优化力度极大，效率几乎达到了极限
求区间里的最小反素数（[1,n]）
这类问题的思路与上一个是一样的，每次不断更新因子的最大个数和最大个数下的最小反素数
