数论—欧几里德算法
What(是什么——定义)
欧几里德算法(Euclidean algorithm)是求两个正整数之最大公因子的算法。
设两数为a、b(a>b),求(a,b)的步骤如下:
①用a除以b,得a=bq+r1(0≤r1)。
②若r1=0,则(a,b)=b;
③若r1≠0,则再用b除以r1,得b=r1q+r2 (0≤r2).若r2=0,则(a,b)=r1,若r2≠0,则继续用r1除以r2,如此下去,直到能整除为止。其最后一个为被除数的余数的除数即为(a, b)。例如:a=25,b=15,a/b=10,b/10=15,10/5=20,最后一个为被除数余数的除数就是5,5就是所求最大公约数。
Why(为什么——证明)
定理:设a,b,c是不全为0的整数,若存在q∈Z,使得a=bq+c,则(a,b)=(b,c)
证明:由(b,c)|b,(b,c)|c及a=bq+c,知(b,c)|a,因此(b,c)是a和b的公因数,但(a,b)是a和b的最大公因数,所以(b,c)<=(a,b),同理可得(b,c)>=(a,b),则(b,c)==(a,b)
利用此定理证明辗转相除法:
设a>0,b>0,令r0=1,r1=b,设:
r0=r1 * q1 + r2
r1=r2 * q2 + r3
.
.
.
rn-2=rn-1 * qn-1 + rn
rn-1=rn * qn
则:(a,b)=(r0,r1)=(r1,r2)=(r2,r3)=…=(rn-1,rn)=(rn,0)=rn
复杂度
——《挑战程序设计竞赛》
代码实现
int gcd(int a,int b)
{
return b?gcd(b,a%b):a;
}
Updata 另外的证明 2019.2.17
感觉看着要舒服一点
总结
总结一下 欧几里得定理比较有意思的一点 就是这样一个结论




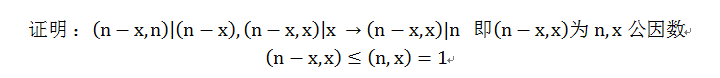




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现