曼哈顿距离（Manhattan Distance ）详解

曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离，即d（i，j）=|xi-xj|+|yi-yj|。对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离。
——引用自百度

简析

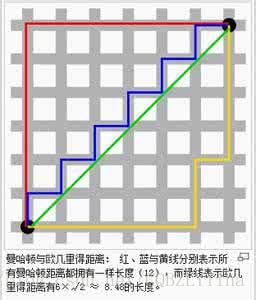
• 就曼哈顿距离的概念来说，只能上、下、左、右四个方向进行移动，而且两点之间的曼哈顿距离是两点之间的最短距离（在只能向上、下、左、右四个方向进行移动的前提下）。为什么呢？假设从一点到达另一点（只能向上、下、左、右四个方向进行移动，下同），要使路程最短，就只能每一步都有用（使之与另一点的南北距离或东西距离缩短），所以我们最先想到的是图中的红线，它的长度就是两点之间的曼哈顿距离。而红线可以通过平移转化为蓝线、黄线等线，它们的长度都与红线相等。（再解释不下去了，体会一下）
• 那么我们可以利用曼哈顿距离解决什么问题呢？曼哈顿距离可以代替一个广搜，不过这个广搜是有条件限制的：
  ①只能上、下、左、右四个方向进行移动（很多迷宫问题其实都有这个特性）
  ②只求两点之间最短路径的长度，不求路径过程
  为了让大家更清晰地体会，举一例题：最少联通代价
  此题本是要用深搜+广搜解决，但巧法可只用一个小深搜+曼哈顿距离思想