【树dp 结论题】Mag 6.22测试COCI

(30%的那个数据 “不会有节点和超过 2 个其他节点直接相连” 意思没怎么看明白 不影响做题(小声BB )
样例:
样例输入 1
2
1 2
3
4
样例输出 1
3/1
样例输入 2
5
1 2
2 4
1 3
5 2
2
1
1
1
3
样例输出 2
1/2
思路:
1.首先 有个结论:
乘法是越滚越大的
只有两种链上才会产生最小的魔法值
一种是一条链上全部都是1
另一种是这一条1上有且只有一个2
(而且2在中间 否则取1较多的那一边就可以 当然 这个在树dp里是不需要我们讨论的
如果没有1和2的话,就是最小的那单独一个点(比如说样例1)
怎么证明呢
首先 全是1的那种情况当然不用说
然后
由于我太弱了 不会证明 所以搬了一个大佬的证明
觉得很有道理 就是不知道为什么要取这两种极端情况
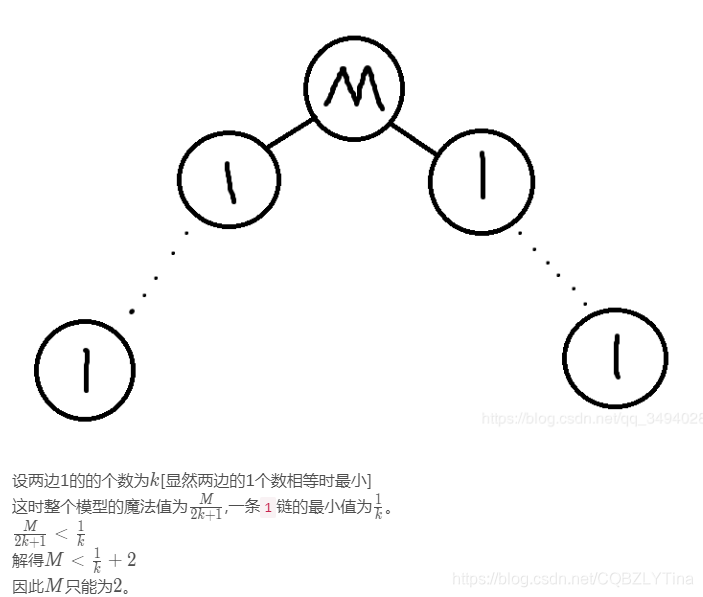
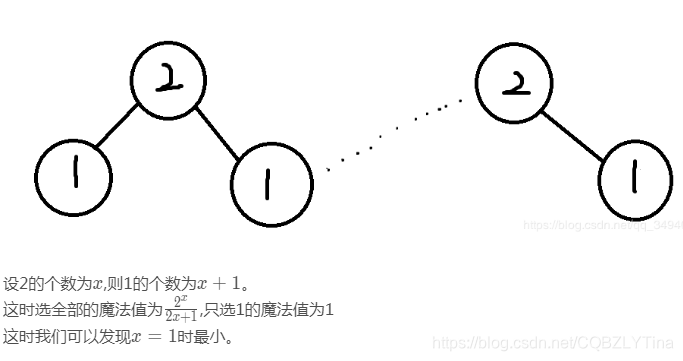
(由于没有当面征求他的同意 所以可能会侵犯他的智力成果权 所以侵删)
Update 2019.6.26
嗯 我自己大概也想了一下 太多了留坑慢慢搬
2.然后就是树dp的部分啦
f[i] 从i点向下延伸能够得到的最长的全1链
g[i]:从i点向下延伸能的最长的有一个为2的链
可以类比一下求树的直径
在一个点时 这条路径可以是最长的全1链和次长的全1链拼在一起的,也有可能是最长的全1链和最长的含2 链拼在一起的
最长的全1链和最长的含2链有可能会重合 也就是都是从同一个子树上搞过来的 所以这里要特判一下
具体转移见注释:
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<string>
#include<queue>
#include<algorithm>
using namespace std;
#define MAXN 1000005
#define LL long long
int n;
//f[i] 从i点向下延伸能够得到的最长的全1链 g[i]:从i点向下延伸能的最长的有一个为2的链
int f[MAXN],g[MAXN],val[MAXN];
int ma=1000000005,mb=1;
vector<int>G[MAXN];
int rd()
{
int f=1,x=0;char c=getchar();
while(c<'0'||'9'<c){if(c=='-')f=-1;c=getchar();}
while('0'<=c&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar();
return f*x;
}
int gcd(int x,int y)
{
if(y==0) return x;
return gcd(y,x%y);
}
void upd(int x,int y)
{
if((double)x/y<(double)ma/mb)
ma=x,mb=y;
}
void dfs(int u,int p)
{
int n1=0/*1的最长链*/,n2=0/*1的次长链*/,n3=0/*含2的最长链*/;
//以上均在u的儿子之中
for(int i=0;i<G[u].size();i++)
{
int v=G[u][i];
if(v!=p)
{
dfs(v,u);
if(val[u]==1)//状态转移
f[u]=max(f[u],f[v]+1),g[u]=max(g[u],g[v]+1);
if(val[u]==2)
g[u]=max(g[u],f[v]+1/*自己就已经是2*/);
if(f[n1]<f[v]) n2=n1,n1=v;
else if(f[n2]<f[v]) n2=v;//没有最长链长 但是比次长链长
if(g[n3]<g[v]) n3=v;
}
}
if(val[u]==1)
{
if(n1==n3)//重合 但是为什么不存含2的次长链呢?
upd(2,g[n3]+f[n2]+1);
else upd(2,g[n3]+f[n1]+1);
upd(1,f[n1]+f[n2]+1);
f[u]=max(f[u],1);//初始化边界
g[u]=max(g[u],1);
}
if(val[u]==2)
{
upd(2,f[n1]+f[n2]+1);
g[u]=max(g[u],1);
}
}
int main()
{
//freopen("mag.in","r",stdin);
//freopen("mag.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n-1;i++)
{
int u,v;
u=rd(),v=rd();
G[u].push_back(v);
G[v].push_back(u);
}
for(int i=1;i<=n;i++)
{
val[i]=rd();
ma=min(ma,val[i]);
}
if(ma!=1&&ma!=2)
{
printf("%d/1",ma);
return 0;
}
dfs(1,0);
int d=gcd(ma,mb);
printf("%d/%d",ma/d,mb/d);
return 0;
}
由于还有一些证明细节自己也没有搞懂
所以
To be continue…




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现