【期望·高斯消元】HNOI2013 游走

题目传送门

容易想到，应该是算出经过每一条边的期望，然后给期望大的赋小的编号，期望小的赋大的编号。
没有其它奇奇怪怪的附加属性，只是随意地走的话，经过边的期望应该只是和图的长相有关联，也就是只和边两边的结点有关，而且边的数量没有限制，最大可以达到$n^2$的级别，所以我们可以用点的期望来算边的期望。
如果知道了点的期望，那么边的期望就是
$点的期望\ast \frac{1}{这个点的边数}$(这条边两个端点这么算的和)
那么就要开始求点的期望了
对于每一个点$x$，设点的期望是$f[x]$，与$x$相邻的有$num[x]$条边，相邻的点是$1至k$，则有下式：

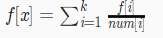
每一个点都可以列出这样的式子，进行高斯消元就可以解出$f[]$了
特殊地，要注意第一个点和第$n$个点
"游走"是从点$1$开始,则计算点$1$期望时实际期望应该是原期望+$1$
到了点$n$不会继续"游走"了 则若有点和$n$相连,那么在计算期望时是不需要将其算入的

#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
#define N 505
int n,m;
double f[N][N],ans[N],q[N*N];
vector<int>G[N];
int F[N*N],T[N*N];
double eps=1e-7;
int rd()
{
	int x=0,f=1;char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return f*x;
}
double Abs(double x)
{
	if(x>0) return x;
	return -x;
}
void Gauss()
{
	for(int i=1;i<n;i++)
	{
		int r=i;
		for(int j=i+1;j<n;j++)
			if(Abs(f[r][i])<Abs(f[j][i]))
				r=j;
		//找这一列系数最大的那一行 
		//每次丢掉的那个都挪到了上面去 所以从i开始就可以 
		if(i!=r) swap(f[i],f[r]);
		double div=f[i][i];//现在第i行是目标 
		for(int j=i;j<=n;j++)
			f[i][j]/=div;//第j个系数化为1
		for(int j=i+1;j<=n;j++)
		{
			div=f[j][i];
			for(int k=i;k<=n;k++)
				f[j][k]-=f[i][k]*div;
		}
	}
	for(int i=n-1;i>=1;i--)
	{//回带 
		ans[i]=f[i][n];
		for(int j=i+1;j<n;j++)
			ans[i]-=(f[i][j]*ans[j]);
		//ans[i]/=f[i][i];
	}
	return ;
}
bool cmp(double a,double b)
{
	return a>b;
}
int main()
{
	n=rd(),m=rd();
	for(int i=1;i<=m;i++)
	{
		int u=rd(),v=rd();
		G[u].push_back(v);
		G[v].push_back(u);
		F[i]=u,T[i]=v;
	}
	f[1][n]=1.0;//第1个点一开始就在 期望是1 
	for(int i=1;i<n;i++)
	{
		f[i][i]=1.0;
		for(int j=0;j<G[i].size();j++)
			if(G[i][j]!=n)
				f[i][G[i][j]]=-1.0/G[G[i][j]].size();
	}
	Gauss();
	for(int i=1;i<=m;i++)
		q[i]=ans[F[i]]/G[F[i]].size()+ans[T[i]]/G[T[i]].size();
	sort(q+1,q+m+1,cmp);
	double res=0;
	for(int i=1;i<=m;i++)
		res+=q[i]*(1.0*i);
	printf("%.3lf\n",res);
}