LOJ6160 美团 CodeM 初赛 Round A 二分图染色【容斥】
题目解析
考试的时候我是在按照点在想，可以把点分成四类：只有绿色边，有一条红色边，有一条蓝色边，有一条红色边和一条蓝色边（后三种其余都是绿色边），然后把\(n\)分解成四个整数的和，再分别计数。但是一个点的情况可能会影响到其它与之有边相连的点，所以不好做。
不要怕，直接来
还是从边的角度来考虑。
由于绿色没有影响，所以我们把它当作不染色。先算只有一种颜色的染色方案。设\(f(n)\)表示对\(n\)个点的二分图的染色方案，由于同一个点只能染一条边，先枚举一个有染色边的点数\(i\)，然后就相当于从这\(n\)个点中选\(i\)个点出来，连到另一边的点去，而另一边的点也不能同时连两条有色边，所以另一边也要选\(i\)个点出来。注意到我一边选点的时候不在乎顺序，但是连到另一边的时候，另一边的点与这一边的点的对应情况不一样，那么连出来的边就不一样，所以另一边的点有顺序。
得到\(f(n)=\sum_{i=0}^nC_n^iA_n^i\)
现在有两种颜色，如果直接算\(f^2(n)\)会把一条边染上两种颜色，现在考虑一下怎么减去不合法的方案。可以用容斥原理，我们钦定一些边让它们被染上两种颜色，总方案数\(=\)钦定\(0\)条边被染两种颜色，其它随便\(-\)钦定\(1\)条边被染两种颜色，其它随便\(+\)钦定\(2\)条边被染两种颜色，其它随便\(……\)
具体而言，\(ans=\sum_{i=0}^n (-1)^i*C(n,i)*A(n,i)*f^2(n-i)\)
\((-1)^i\)是容斥系数，\(C(n,i)*A(n,i)\)是钦定\(i\)条边出来染两种颜色，原理同上，\(*f^2(n-i)\)是剩下的边随便染色。
组合数可以预处理，但是\(f( i)\)要\(n^2\)求，现在，我们就有了一个\(n^2\)的优秀算法。
瓶颈在\(f(i)\)的求法，我们考虑能不能不用通项公式，而是\(O(n)\)递推出来。
我们考虑在\(n-1\)对点的外面再加上一对点会有哪些方案：
- 新加点的边不染色，方案数是\(f(n-1)\)
- 新加点之间的边染色，方案数是\(f(n-1)\)
- 新加点的其中一个与另一边原来的\(n-1\)个点之间的边选一条染色，方案数是\((n-1)f(n-1)\)
- 同理，新加点的另一个与另一边原来的\(n-1\)个点之间的边选一条染色，方案数是\((n-1)f(n-1)\)
- 上面四种情况的方案数加起来，我们发现\(4,5\)可能与原来的点存在冲突，也就是我其中一个点和另一边原来点连边的时候，那个原来点可能与另一个原来点已经有染色边。这个怎么解决呢？我们可以假设如果有冲突，就把冲突的点连给另外那个新增点。举个例子：\(a,b\)是新增点，\(a\)往对面的原来点\(x\)连边，而\(x\)又已经与原来点\(y\)有一条染色边，那么我们把\(x-y\)这条边改成\(b-y\)。这样改动之后，不会有冲突，但是\(4,5\)中有算重的方案，所以我们还要减去：\(a\)与对面原来\(n-1\)个点连边，且\(b\)与对面\(n-1\)个点连边的方案数（这其实是一个小容斥），为\((n-1)^2*f[n-2]\)
然后得到递推关系\(f(n)=2n*f(n-1)-(n-1)^2*f[n-2]\)
（因为我懒，没有画图XD，所以不太清楚的地方可以手动画图~
转化一下问题
棋盘问题可以转化为二分图来解决，那么这个二分图也可以转化为棋盘。
把二分图的\(X\)部放在\(x\)轴，\(Y\)部放在\(y\)轴，那么每一个格点就代表了一条边，我们对格点染色。
同种颜色的边不能在一个结点上，也就是同一行同一列只能有一个这个颜色，就是在棋盘上放车的问题。
同样地，先考虑一种车，可以得到\(f(n)=\sum_{i=0}^nC_n^iA_n^i\)，即在\(n\)行中选出\(i\)行放车，选出来之后它们的列可以顺次有\(n,n-1,n-2...n-i+1\)种选择，当然也可以理解成有顺序地选。（这个似乎比二分图染色直观一点
还是一样的容斥，钦定有\(i\)个两个颜色的车放在了同一个格点。\(ans=\sum_{i=0}^n (-1)^i*C(n,i)*A(n,i)*f^2(n-i)\)
同样的考虑递推式。从\(f(n-1)\)到\(f(n)\)相当于外面多了一圈格点共\(2n-1\)个出来。
我们枚举选择周围的一圈格点，然后删掉那一行一列，剩下的\(n-1\)行，\(n-1\)列化归成\(f(n)\)
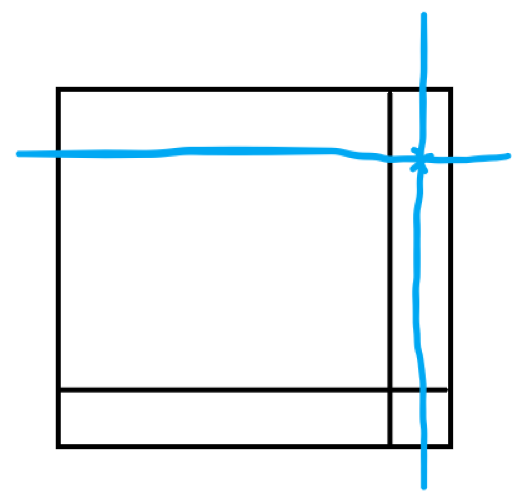
还有一种方案是外面这一圈一个都不选，所以一共有\(2n\)种，再乘上化归之后的\(f (n-1)\)
那个，我之前想错了，我以为是外面这一圈是或者的关系，然后乘上里面的那个原来的\(n-1\)的棋盘，那这样的方案（如下图）就没有办法算：
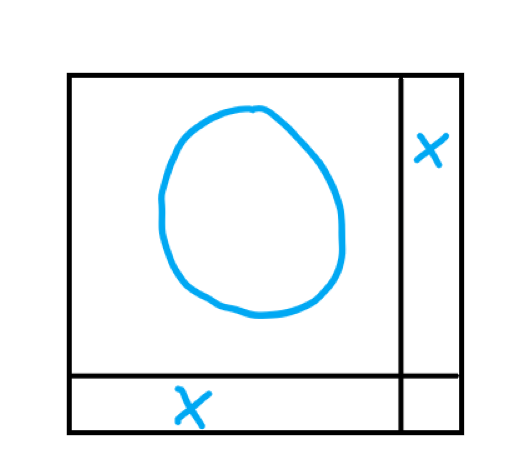
但实际上是可以的，按照前面的正确思路理解，就是删掉选中的那一行那一列，剩下的最后一列还是在化归的方案里。
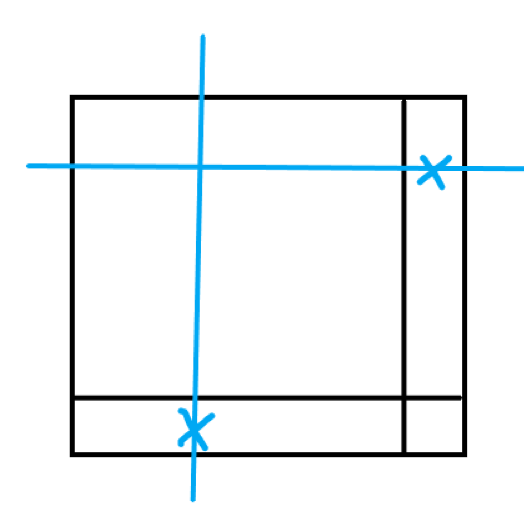
但是还是有算重的情况，就是下图的情况，它在行，列里面都算过，要减去。
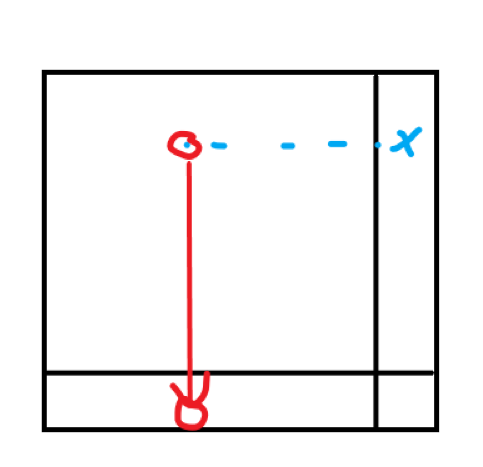
（其实也可以想成之前的那种替换的想法，如果有冲突，就把冲突的点搬走，然后就相当于有了多出来的行列都有格子选的情况，但是这样会算重，就是一种方案可以是由行来算，冲突搬到列去，也可以是列来算，把冲突搬到行里去）
►Code View
#include<cstdio>
#include<algorithm>
#include<queue>
#include<set>
using namespace std;
#define N 10000005
#define MOD 1000000007
#define INF 0x3f3f3f3f3f3f3f3f
#define LL long long
LL rd()
{
LL x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-') f=-1; c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48); c=getchar();}
return f*x;
}
int n;
LL fac[N],inv[N],f[N];
LL ksm(LL a,LL b)
{
LL res=1ll;
while(b)
{
if(b&1) res=res*a%MOD;
a=a*a%MOD;
b>>=1;
}
return res;
}
void Init()
{
fac[0]=1,inv[0]=1;
for(int i=1;i<=N-5;i++)
fac[i]=fac[i-1]*i%MOD;
inv[N-5]=ksm(fac[N-5],MOD-2);
for(int i=N-6;i>=1;i--)
inv[i]=inv[i+1]*(i+1)%MOD;
}
LL C(int a,int b)
{
return fac[a]*inv[a-b]%MOD*inv[b]%MOD;
}
LL A(int a,int b)
{
return fac[a]*inv[a-b]%MOD;
}
int main()
{
n=rd();
Init();
f[0]=1,f[1]=2;//边界 一条边 染/不染
for(int i=2;i<=n;i++)
f[i]=(2ll*i*f[i-1]%MOD-1ll*(i-1)*(i-1)%MOD*f[i-2]%MOD+MOD)%MOD;
//for(int i=2;i<=n;i++)
// printf("%lld\n",f[i]);
LL ans=0;
for(int i=0;i<=n;i++)
{
LL res=C(n,i)*A(n,i)%MOD*f[n-i]%MOD*f[n-i]%MOD;
if(i&1) ans=(ans-res+MOD)%MOD;
else ans=(ans+res)%MOD;
}
printf("%lld\n",ans);
return 0;
}
/*
f(n)=sum i=0->n C(n,i)*A(n,i)
ans= sum i=0->n (-1)^i*C(n,i)*A(n,i)*f(n-i)^2
f(n)=2n*f(n-1)-(n-1)^2*f(n-2)
*/
