最小乘积生成树
题目解析
想法还是比较难想到的。
把每棵生成树的\(\sum a_e\)和\(\sum b_e\)看成点对\((x,y)\)，于是答案是\(k=x\times y\)最小的点对。由于边权都是非负数，所以可以看成是离坐标轴最近的反比例函数的系数。
怎么求这个点呢？
首先，分别找到离\(x\)轴，\(y\)轴最近的点
这个可以分别以\(a_e,b_e\)作为边权，求\(MST\)
不妨设离\(x\)轴最近的点是\(A\)，离\(y\)轴最近的点是\(B\)
然后，找到一个在\(AB\)左下方，并且离\(AB\)最远的点\(C\)
可以等价为\(S_ΔABC\)最大，因为底为\(AB\)是定值，三角形面积越大，高越大，而高就是距离。
根据叉乘的几何意义，\(S_ΔABC=\frac{|\vec{AB}\times\vec{AC}|}{2}\)
注意到\(\vec{AB}\times\vec{AC}\)是负数：（我还想了很久为啥它是负数，我一直以为叉乘顺序不一样（旋转方向不一样）只会影响最后生成的向量的方向（右手螺旋定理），但注意这里是有向面积）
如果是\(\vec{AB}\times\vec{AC}\)，那么就是\(\vec{AB}\)逆时针转到\(\vec{AC}\)，转了优角，所以\(sinθ<0\)，所以\(\vec{AB}\times\vec{AC}=|\vec{AB}|\times|\vec{AC}|\times sinθ<0\)
反之，如果是\(\vec{AC}\times\vec{AB}\)，就是\(\vec{AC}\)逆时针转到\(\vec{AB}\)，转了劣角，所以乘出来\(>0\)
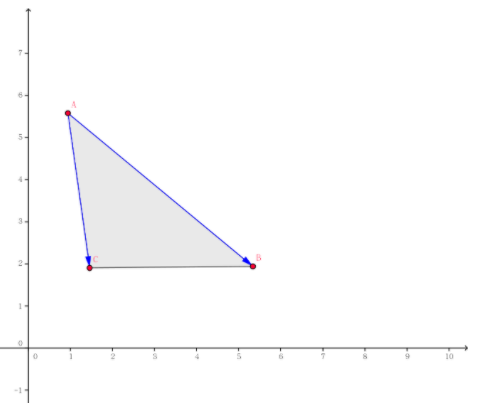
（图片来自于网络）
所以\(S_ΔABC=-\frac{\vec{AB}\times\vec{AC}}{2}\)，要最大化\(S_ΔABC\)，只需要最小化\(\vec{AB}\times\vec{AC}\)
根据叉乘的坐标表达形式：\(\vec{AB}\times\vec{AC}\\=(x_B-x_A)(y_C-y_A)-(x_C-x_A)(y_B-y_A)\\ =(x_B-x_A)y_C+(y_A-y_B)x_C-(x_B-x_A)y_A+(y_B-y_A)x_A\)
后面是常数，所以要最小化\((x_B-x_A)y_C+(y_A-y_B)x_C\)，\(x_C,y_C\)是生成树的\(\sum\)，所以把边权赋成\((x_B-x_A)b_e\)和\((y_A-y_B)a_e\)，然后求\(MST\)就可以得到\(C\)的坐标，用\(C\)的坐标更新答案。
递归AC,BC
把\(AC,BC\)拿去重复上述操作，递归处理，不断得到一个新的\(C\)，更新答案。
直到算出来的\(C\)满足\(\vec{AB}\times\vec{AC}\)，说明转过火了，这个时候的\(C\)在\(AB\)上方，结束递归。
点的编号居然是从\(0\)开始的，差评（雾
►Code View
#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<cstring>
using namespace std;
#define N 205
#define M 10005
#define INF 0x3f3f3f3f
#define LL long long
int rd()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1; c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
return f*x;
}
int n,m,f[N];
struct node{
int u,v,a,b,w;
}e[M];
struct Point{
int x,y;
};
Point ans;
int Cross(Point p,Point q)
{
return p.x*q.y-p.y*q.x;
}
bool cmp(node p,node q)
{
return p.w<q.w;
}
void Init()
{
for(int i=1;i<=n;i++)
f[i]=i;
}
int Find(int x)
{
if(f[x]==x) return x;
return f[x]=Find(f[x]);
}
bool Union(int u,int v)
{
u=Find(u),v=Find(v);
if(u==v) return 0;
if(u<v) f[u]=v;
else f[v]=u;
return 1;
}
Point Kruskal()
{
Point res; res.x=0,res.y=0;
Init();
sort(e+1,e+m+1,cmp);
int cnt=0;
for(int i=1;i<=m;i++)
{
if(!Union(e[i].u,e[i].v)) continue;
res.x+=e[i].a,res.y+=e[i].b;
cnt++;
if(cnt==n-1) break;
}
LL ret=1ll*ans.x*ans.y,now=1ll*res.x*res.y;
if(now<ret||(now==ret&&res.x<ans.x)) ans=res;
return res;
}
void solve(Point A,Point B)
{
for(int i=1;i<=m;i++)
e[i].w=(B.x-A.x)*e[i].b+(A.y-B.y)*e[i].a;
Point C=Kruskal();
Point D,E;
D.x=B.x-A.x,D.y=B.y-A.y;
E.x=C.x-A.x,E.y=C.y-A.y;
if(Cross(D,E)>=0) return ;
solve(A,C);
solve(C,B);
}
int main()
{
n=rd(),m=rd();
for(int i=1;i<=m;i++)
e[i].u=rd()+1,e[i].v=rd()+1,e[i].a=rd(),e[i].b=rd();
for(int i=1;i<=m;i++)
e[i].w=e[i].a;
ans.x=INF,ans.y=INF;
Point A=Kruskal();
for(int i=1;i<=m;i++)
e[i].w=e[i].b;
Point B=Kruskal();
solve(A,B);
printf("%d %d\n",ans.x,ans.y);
return 0;
}
