USACO 2020 OPEN Favorite Colors【并查集-启发式合并-思考】
题意简述
仰慕喜欢同色奶牛的奶牛喜欢同色 (禁止套娃 ,求一种方案,奶牛喜欢的颜色种数最多,多种方案求字典序最小。
题目解析
这道题我最先想到的居然是二分+并查集,我在想啥
咳咳
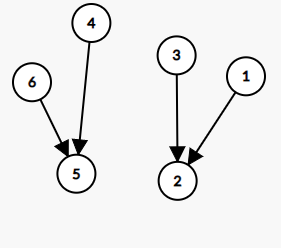
首先,考虑一个比较简单的情况,假如图长这样:
仰慕关系:\(6,4\)仰慕\(5\),\(3,1\)仰慕\(2\)
同一头奶牛喜欢的颜色当然是相同的,\(6,4\)仰慕对象的喜好颜色一样,所以\(6,4\)喜欢的颜色一样,同理\(3,1\)喜欢的颜色一样。我们把他们用并查集套起来,数有几个块就可以了
然后考虑更复杂的情况:

如图,\(4\)是一只花心的奶牛,它不仅仰慕\(5\),还仰慕\(2\)。
同一头奶牛喜欢的颜色当然是相同的,\(4\)只有一种喜欢的颜色,而\(6\)和\(4\)喜欢颜色一样,因为它们都喜欢\(5\),同理,\(3,1\)喜好颜色也和\(4\)一样,那么两个连通块就通过\(4\)联通了。
为了方便写代码,我们这样看这个图:(就是把边反了个向,好写代码
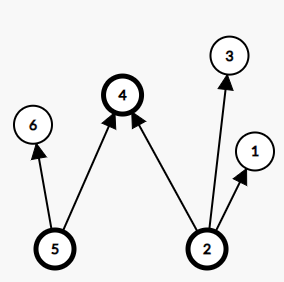
从两只站在仰慕链顶端的牛出发(其实也不一定是从它们出发,反正所有牛的儿子都要并在一起,话说也不一定有站在仰慕链顶端的牛,没有保证是\(DAG\)),把它们的儿子并在一起,如果碰到了\(4\)这样的花心结点,就把两个并查集合在一起。
至于原图,一个并查集里的点可以当成一个点来处理,也就是要缩点。具体的方法很暴力,就是把别人的儿子接到我这里来,然后把别人和它的儿子都从图里删掉。为了保障复杂度,用启发式合并,也就是小的集合合并到大集合上去。
►Code View
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
#define LL long long
#define N 200005
#define INF 0x3f3f3f3f
int rd()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1; c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48); c=getchar();}
return f*x;
}
vector<int>G[N];
int n,m,f[N]/*连通块的大小 启发式合并要用到 初始为-1 表示自己是根*/,c[N];
int Find(int x)
{
if(f[x]<0) return x;
return f[x]=Find(f[x]);
}
void dfs(int u)
{
if(G[u].size()<2) return ;
int x=Find(G[u][0]);
for(int i=1;i<G[u].size();i++)
{
int y=Find(G[u][i]);
if(x==y)continue;
if(f[x]<=f[y])
{
f[x]+=f[y];
f[y]=x;
for(int j=0;j<G[y].size();j++)
G[x].push_back(G[y][j]);
G[y].clear();
}
else
{
f[y]+=f[x];
f[x]=y;
for(int j=0;j<G[x].size();j++)
G[y].push_back(G[x][j]);
G[x].clear();
x=y;
}
}
G[u].clear();
G[u].push_back(x);
dfs(x);
}
int main()
{
memset(f,-1,sizeof(f));
n=rd(),m=rd();
for(int i=1;i<=m;i++)
{
int u=rd(),v=rd();
G[u].push_back(v);
}
for(int i=1;i<=n;i++)
dfs(i);
int cnt=0;
for(int i=1;i<=n;i++)
{
int fa=Find(i);
if(!c[fa]) c[fa]=++cnt;
printf("%d\n",c[fa]);
}
return 0;
}
转载请注明出处,有疑问欢迎探讨
博主邮箱 2775182058@qq.com


 浙公网安备 33010602011771号
浙公网安备 33010602011771号