USACO20FEB Equilateral Triangles P【思维-曼哈顿距离-切比雪夫距离】
题意简述
求任意两点之间曼哈顿距离相等的无序三元组个数。
题目解析
Step.1
首先，有个结论：平面上到点\((x,y)\)的曼哈顿距离为\(d\)的点的轨迹，是以\((x,y)\)为中心，\(2d\)为对角线的正方形。（就是图中的四边形\(BCDE\)
这个应该比较好看，点在正方形上滑动时，纵坐标\(±1\)，横坐标也\(±1\)。更确切地说，横坐标离\(A\)远\(1\)，纵坐标就离\(A\)近\(1\),横坐标离\(A\)近\(1\)，纵坐标就离\(A\)远\(1\)。
但是菱形是斜着的，不好做，所以我们旋转一下，“拨乱反正”，把\((x,y)\)变成\((x+y,x-y)\)。
这大概也是为啥好多题解都在说可以转化为切比雪夫距离的本质原因吧。
Step.2
又有个结论：\((x,y)\)转化坐标系\(->(x+y,x-y)\)，原坐标系的曼哈顿距离=新坐标系的切比雪夫距离
简单说明一下：
两点\((x1,y1),(x2,y2)\)
原坐标系的曼哈顿距离\(=|x1-x2|+|y1-y2|\)
新坐标系的切比雪夫距离\(=max(|x1+y1-x2-y2|,|x1-y1-x2+y2|)=max(|x1-x2+y1-y2|,|x1-x2-(y1-y2)|)\)
讨论一下\(x1-x2\)和\(y1-y2\)的符号和绝对值大小即可。
令\(x1-x2=m,y1-y2=n\)（写起来方便
\(m,n\)同号时,\(|m+n|=|m|+|n|,|m-n|=||m|-|n||\)
注意到，无论\(|m|,|n|\)大小关系如何，\(|m-n|=(|m|-|n|)/(|n|-|m|)\)都是要小于\(|m|+|n|\)的，得证。
\(m,n\)异号时，\(|m+n|=||m|-|n||,|m-n|=|m|+|n|\)，同理。
另外一个相似的结论，也补充在这里吧（这道题没有用到）：\((x,y)->(\frac{x+y}2,\frac{x-y}2)\)，原坐标的切比雪夫距离=新坐标的曼哈顿距离，证明同理。
当然，这是从代数角度的理解方式，我觉得可以从几何来看更简单。
前面说到，正方形\(BCDE\)是满足曼哈顿距离为\(d\)的轨迹。
那如果把轨迹摆正，把正方形上每一个点都按照\((x,y)->(x+y,x-y)\)映射（转换坐标系），画出来一个以\(2d\)为边长的正方形，而由几何关系（看图）易知，这个正方形是到\(A\)点切比雪夫距离为\(d\)的点的轨迹。
Step.3
符合条件的三元组一定有两个点\(x\)或\(y\)坐标相同。
如果先选出两个不满足上述要求的点\(A,B\)
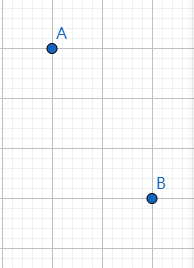
图中标注出来的\(T,U\)是符合条件的第三者点，它们均满足上述条件。(\(A\)点符合条件的点是以\(A\)为中心的边长为\(3\)的正方形，\(B\)同理，所以满足条件的点是两个正方形轨迹的交点)（我画得有亿点点乱
Step.4
那么，符合条件的三元组长这个样子：
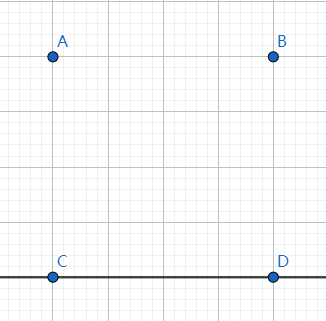
线段上所有的整点都符合条件。
可以枚举\(A,B\)点，由于\(A,B\)的\(x/y\)坐标相同，这个复杂度是\(O(n^3)\)的，至于算\(CD\)之间有多少个点，这个可以用前缀和维护。
\(x,y\)坐标相同分别算一遍，但是\(ABC,BCD,ABD,BDA\)会被算两次（即边界点会重复计算），那么就在第二次枚举的时候，不把边界点算进去就可以了。
Step.5
其实完全可以不用转化坐标系，直接拿原来那个斜着的坐标做也可以，只不过写起来麻烦一点罢了，而且要旋转四个方向，但是不用思考中间那一坨推导。
不过见过这种东西的话，做题会方便很多。
►Code View
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
#define LL long long
#define N 305
#define DEL 100000
#define INF 0x3f3f3f3f
int rd()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1; c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48); c=getchar();}
return f*x;
}
int n,ans;
char mp[N][N];
int a[N<<1][N<<1],s1[N<<1][N<<1],s2[N<<1][N<<1];
int main()
{
n=rd();
for(int i=1;i<=n;i++)
{
scanf("%s",mp[i]+1);
for(int j=1;j<=n;j++)
if(mp[i][j]=='*')
a[i+j][i-j+n]=1;//转化为切比雪夫距离 防止负数 平移坐标
}
n*=2;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
s1[i][j]=a[i][j]+s1[i][j-1],s2[i][j]=a[i][j]+s2[i-1][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(a[i][j])//第一个奶牛点
for(int k=j+1;k<=n;k++)//第二个奶牛点 和第一个点i相同
if(a[i][k])
{
int d=i+(k-j);
if(d<=n) ans+=s1[d][k]-s1[d][j-1];
d=i-(k-j);
if(d>=1) ans+=s1[d][k]-s1[d][j-1];
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(a[j][i])
for(int k=j+1;k<=n;k++)
if(a[k][i])
{
int d=i+(k-j);
if(d<=n) ans+=s2[k-1][d]-s2[j][d];//要挖掉边界点 在前面算过
d=i-(k-j);
if(d>=1) ans+=s2[k-1][d]-s2[j][d];
}
printf("%d\n",ans);
return 0;
}
