【kmp-循环节】ARC060D 最良表現/Best Representation
题意简述
某谷的题意太绕了qwq
若一个字符串\(s\)存在长度小于\(|s|\)循环节，我们称它是一个好串。
现在要把\(s\)分割成若干段，要求每一段都是一个好串。
所有满足条件的分割方案中，分割段数最小的那个方案被称为“全场最佳”。
求“全场最佳”的分割段数以及“全场最佳”的方案数。
题目解析
首先考虑怎么把循环节给搞出来。
这个可以用\(kmp\)的失配数组来做。
如果一个长度为\(n\)的串\(s\)由\(k\)个相同的长度为\(len\)的子串\(t\)拼接而成，并且\(t\)是\(s\)可以划分的最小循环串，那么一定有\(s[1...n-len]=s[len+1...n]\)（前\(k-1\)个子串拼在一起等于后\(k-1\)个子串拼在一起）
并且根据失配数组（\(p[]\)）的定义可以知道，\(p[n]\)就是去掉最后一个\(t\)的前一个位置。
所以\(len=n-p[n]\)
那么只需要判断\(len|n\)就知道是否有循环节了
然后考虑这道题。
如果没有循环节，那么很显然答案就是不分割，\(1 \ \ \ 1\)
如果循环节为\(1\)，那么就要全部分开 答案就是\(\ n \ \ \ 1\)
如果有不为\(1\)的循环节，那么可以从某个循环节的中间断开，分成\(2\)段。
刚开始还以为可以直接算答案，所以我是这么写的：
int k=len/m;
if(k==2) k--;
int ans=len-1-(k-1);
printf("2\n%d\n",ans);
然后\(WA\)掉了才发现有这样的情况：
\(aabab\ aabab->aabab\ a\ |\ \ abab\) 右边是循环串
发现总方案数不超过\(n-1\)（所以\(1e9+7\)是模了个寂寞）可以枚举一个断点来看是否满足左右两边都不循环
所以还需要倒着做一遍\(kmp\)，用之前的方法判断左右两个子串是否为循环串。
由于\(t\)是最小循环节，所以可以证明至少存在一种方案满足条件（分类讨论循环次数为\(2\)和大于\(2\)），所以\(2\)是最小答案。
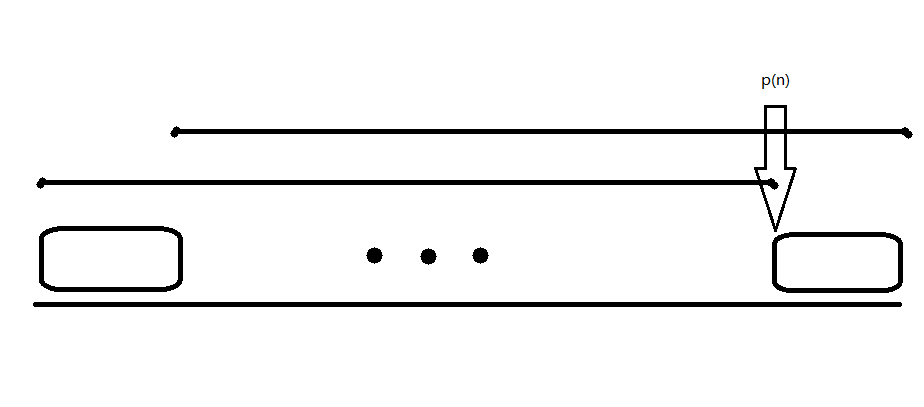
还是简单说一下：循环次数为\(2\)时，从两个循环节之间劈开就可以，因为\(t\)是最小循环节，所以两个子串一定不循环；循环次数大于\(2\)时，可以把它分成\(2\)部分，一段字符串\(+1\)个字符的形式，那么显然结尾的\(1\)个字符不循环，接下来证明开头的那一个字符串一定不循环。假设开头的字符串循环，可以画一个图大概看一下，利用两个循环关系对应位置上的数相等，可以导出存在一个更小的循环节，而这与\(t\)是最小的循环节相矛盾，所以开头的字符一定不循环。
方框是一个循环节，蓝色线段是另外一个循环节（一个是刚开始的，另一个是去掉最后一个字符的循环节）根据对应关系可以得出这些红色的线段都是相等的：
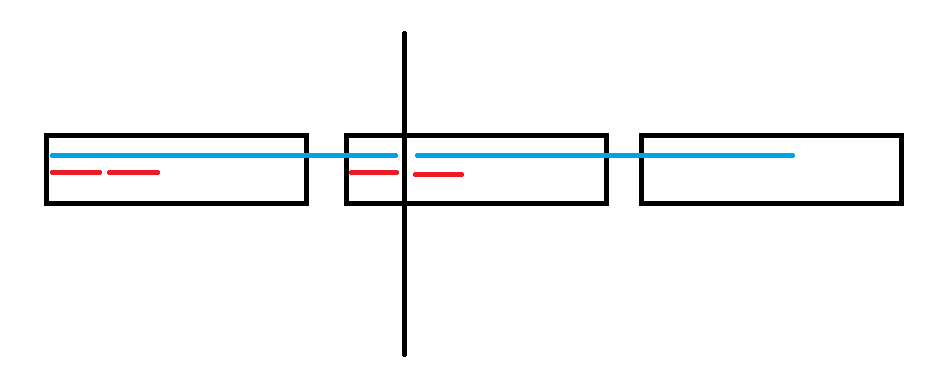
然后你发现两条蓝色的线段是相等的，而其中一条蓝色线段有两条红色线段，另一条蓝色线段只有一条红色线段，于是可以对应得到剩下那一部分是红色线段，然后在根据剩下的黑框框相等得到左边那个黑框框的下一部分也是红色线段...然后套娃下去。
并且红色线段的长度是黑框框的长度和蓝色线段长度的因数，所以红色线段一定是一个循环节，所以存在一个更短的循环节，与\(t\)是最小的循环节相矛盾。
updated:
然后路过的大佬给了我一个数学上的思路：（果然数学好和数学不好的人的差距就出来了）
假设两个循环节的长度分别为\(x,y\)，那么有\(S_i=S_{i+x},\ S_i=S_{i+y}\)
组合一下，\(S_i=S_{ax+by}\),\(b\)可以取一切整数（包括负数，相当于线性组合）
那么\(S_i=S_{gcd(x,y)}\)
而\(x≠y\)，则\(gcd(x,y)≠x,gcd(x,y)≠y\)
所以存在一个更小的循环节。
最后我写的时候\(kmp\)倒过来的时候写掉了一行，（注释里有），改了好久，还是要多谢大佬orz
►Code View
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#include<string>
#include<map>
#include<cmath>
using namespace std;
#define N 500005
#define MOD 1000000007
#define LL long long
int rd()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1; c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48); c=getchar();}
return f*x;
}
char s[N];
int p[N],q[N];
int j,len;
bool check1(int i)
{
int t=i-p[i];
if(i==t||i%t) return 1;
return 0;
}
bool check2(int i)
{
int t=q[i]-i;
if((len-i+1)==t||(len-i+1)%t) return 1;
return 0;
}
int main()
{
scanf("%s",s+1);
p[1]=0;
j=0,len=strlen(s+1);
//表示1...j 和 len-j+1...len 可以匹配
for(int i=2;i<=len;i++)
{//求失配数组
while(j>0&&s[j+1]!=s[i]) j=p[j];
if(s[j+1]==s[i]) p[i]=j+1;
else p[i]=0;
j=p[i];
}
j=len+1,q[len]=len+1;
for(int i=len-1;i>=1;i--)
{
//printf("%d\n",i);
while(j<len+1&&s[j-1]!=s[i]) j=q[j];
if(s[j-1]==s[i]) q[i]=j-1;
else q[i]=len+1;//啊 这里打掉了
j=q[i];
}
int m=len-p[len];
if(m==1)
{
printf("%d\n1\n",len);
return 0;
}
if(len%m||len==m)
{
puts("1"); puts("1");
return 0;
}
int ans=0;
for(int i=1;i<=len-1;i++)
if(check1(i)&&check2(i+1)) ans++;
printf("2\n%d\n",ans);
return 0;
}
