Miller Rabin素数测试和Pollard Rho算法
翻了好多博客和题解,感觉都讲得不是很清晰qwq,很多地方就一个显然轻飘飘地带过,自己想了好久才想通。
素性测试
算法是一种高效的单个质数判定方法。虽然是一种不确定的质数判断法,但是在选择多种底数的情况下,正确率是可以接受的。它可以判定的数字范围较大,速度也比较优秀,所以是一种比较实用的算法。
前置定理
费马小定理
若是质数,则,如果不是的倍数,还可以写成,这种写法更常见一些。
二次探测定理
若是素数且,则满足或
证明:
因为,所以,则
又因为是质数,所以或有因子,则或
或
或
算法分析
设我们要判定的数为,我们用一个素数来进行判定。
首先,如果,那么是素数;如果,那么不是素数。可以特判掉。
然后,先用费马小定理进行测试(这一步也叫做费马测试),如果,那么不是质数。
否则,我们用二次探测定理进行测试。
令,如果,显然有,因为这个式子等价于,就是费马小定理,刚才已经判断过了。
令,根据二次探测定理,如果,那么不是素数。
如果,那么把看作是新的一个条件,如果,将,继续重复刚才的内容,判定;当然,如果已经是奇数,那么无法继续判定,所以认定是素数。
如果,不符合二次探测定理的那个条件式,那么就没有办法继续判定,所以认定是素数。
以上就是的算法流程了。
事实上存在很少一部分强伪素数是没有办法被算法筛掉,所以可以多选几个底数进行判定,它能逃脱所有底数的筛选的概率很小,正确率是在可接受范围内的。
经过大佬的经验传授,如果,取就可以。
如果取就可以。
Code View
const int P[]={2,3,5,7,11,13,17,19,23},pn=9;
int ksm(int a,int b,int MOD)
{
int res=1;
while(b)
{
if(b&1) res=1ll*res*a%MOD;
a=1ll*a*a%MOD;
b>>=1;
}
return res;
}
bool check(int x,int p)
{
if(ksm(p%x,x-1,x)!=1) return 0;
int k=x-1,t;
while(!(k&1))
{
k>>=1;
t=ksm(p%x,k,x);
if(t!=1&&t!=x-1) return 0;
if(t==x-1) return 1;//不符合二次探测的条件式 没有办法继续判定
}
return 1;//k变成了奇数 仍然没有筛出来
}
bool Miller(int x)
{
for(int i=1;i<=pn;i++)
{
if(x==P[i]) return 1;
if(x%P[i]==0) return 0;
if(!check(x,P[i])) return 0;
}
return 1;
}
在快速幂会的情况下,可以先把提出来,然后逆着做,倒着乘过去。
算法
算法是一个大数质因数分解算法,它的实现是基于素性测试。它是一种比较玄学的随机化算法,《算法导论》给出的时间复杂度是的,是的一个最小因子。
算法分析
设我们要分解的数是。
首先,我们用判断一下是否为质数,如果是,那么就可以统计信息然后返回。
接下来,我们考虑如果可以找到一个数使得,就是的一个非平凡因子,然后可以把分成和两部分进行递归计算。
然后考虑怎么求这个。首先随机化一个数,然后生成一个序列,其中是一个伪随机数函数,例如,是常数。
是会形成一个环的,环的最长长度是,因为最长到第个数时就会重复,而这个映射关系是唯一的,所以就会成环。
根据生日悖论,环长的期望是,所以复杂度可以保证。不过这个结论我不知道怎么证它,所以大概可以用一个期望来验证的方法来说明它是对的?
定义表示序列已经排到了第个数,中的数都互不相同形成的环长的期望。
那么
前面是和的数一样产生的期望,和一样环长是,和一样环长是...概率是一样的,所以求一个平均值就是期望;后面是和前面的数都不一样的产生的期望。
我们可以写出代码:
double f[N];
void work()
{
int x=rd();
f[x+1]=x;
for(int i=x;i>=1;i--)
f[i]=1.0*(i-1.0)/x*i/2+1.0*(x-i+1)/x*f[i+1];
printf("%.9f\n%.9f",f[1],f[1]*f[1]);
}
实际结果的话,比小,大概是结果的到倍。
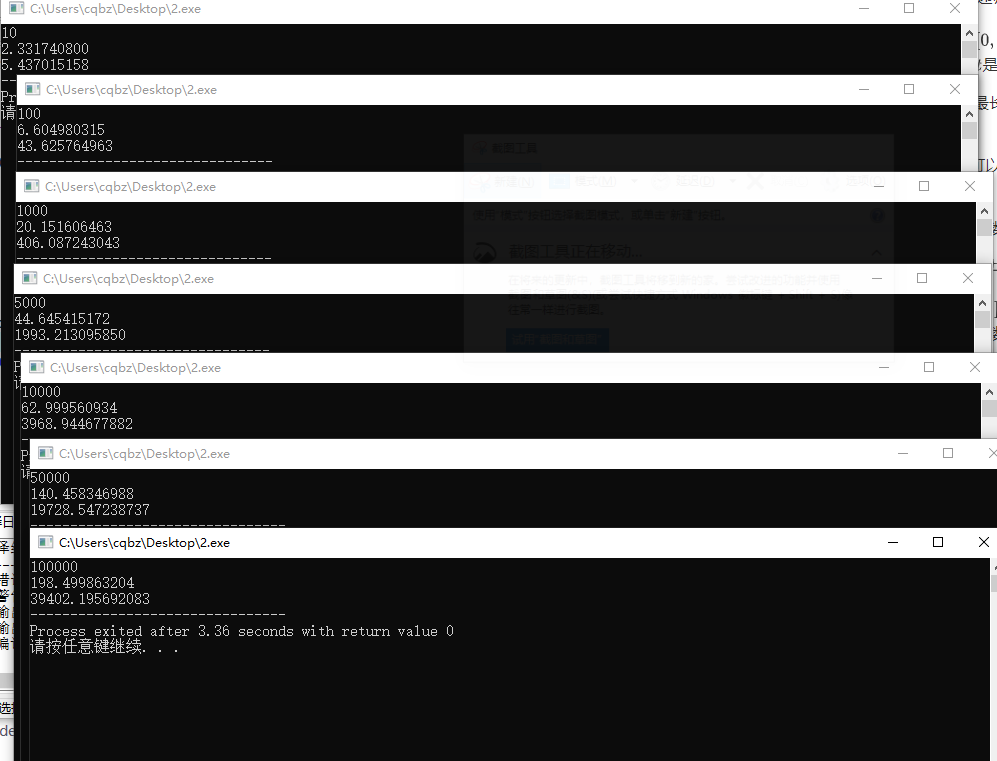
对于求出来的,算出,并判断,如果满足就记录并继续递归计算。
如果已经成环了,就没用了,就分解失败,可以调整的值并重新分解。
关于如何探测环的出现,一个稍微有点暴力的方法是每次都存下来,判断是否有出现过,但这样做在数据范围比较大的时候会。一种比较有意思的做法是提出来的(怎么又是他)。在一个很长的圆形轨道上行走,要判断什么时候至少走了一圈,我们可以让同时从同一起点开始走,的速度是的两倍,当第一次赶上的时候,就走了至少一圈了(准确地来说,应该是2圈?)。
优化:我们每求出一个就求了一个,求得太过频繁,我们完全可以把很多个数累在一起求,不会影响正确性。因为如果,那么
Code View
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#include<iostream>
#include<cstdio>
#include<cmath>
#include<map>
using namespace std;
#define INF 0x3f3f3f3f
#define LL long long
LL rd()
{
LL x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1; c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48); c=getchar();}
return f*x;
}
LL ans;
LL Abs(LL x)
{
if(x>=0) return x;
return -x;
}
LL gcd(LL a,LL b)
{
if(b==0) return a;
return gcd(b,a%b);
}
LL qmul(LL x,LL y,LL MOD)
{//快速乘
return (x*y-(long long) ((long double) x/MOD*y)*MOD+MOD)%MOD;
}
const int P[]={0,2,3,5,7,11,13,17,19,23},pn=9;
int ksm(int a,int b,int MOD)
{
int res=1;
while(b)
{
if(b&1) res=1ll*res*a%MOD;
a=1ll*a*a%MOD;
b>>=1;
}
return res;
}
bool check(LL x,LL p)
{
if(ksm(p%x,x-1,x)!=1) return 0;
LL k=x-1,t;
while(!(k&1))
{
k>>=1;
t=ksm(p%x,k,x);
if(t!=1&&t!=x-1) return 0;
if(t==x-1) return 1;
}
return 1;
}
bool Miller(LL x)
{
for(int i=1;i<=pn;i++)
{
if(x==P[i]) return 1;
if(x%P[i]==0) return 0;
if(!check(x,P[i])) return 0;
}
return 1;
}
void Rho(LL x)
{//
if(Miller(x))
{
ans=max(x,ans);
return ;
}
LL t1=rand()%(x-1)+1;
LL t2=t1,b=rand()%(x-1)+1;
t2=(qmul(t2,t2,x)+b)%x;
LL p=1,i=0;
while(t1!=t2)
{
i++;
p=qmul(p,Abs(t1-t2),x);
if(p==0)
{
LL t=gcd(Abs(t1-t2),x);
if(t!=1&&t!=x)
{
Rho(t);
Rho(x/t);
}
return ;
}
if(i%127==0)//为什么是127...玄学
{
p=gcd(p,x);
if(p!=1&&p!=x)
{
Rho(p);
Rho(x/p);
return ;
}
p=1;
}
t1=(qmul(t1,t1,x)+b)%x;
t2=(qmul(t2,t2,x)+b)%x;
t2=(qmul(t2,t2,x)+b)%x;
}
p=gcd(p,x);
if(p!=1&&p!=x)
{
Rho(p);
Rho(x/p);
return ;
}
}
int main()
{
int T=rd();
while(T--)
{
LL x=rd();
if(Miller(x))
{
puts("Prime");
continue;
}
ans=0;
while(ans==0)
Rho(x);
printf("%lld\n",ans);
}
return 0;
}
(MR还好,PR就是真的脑壳大




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
2019-08-14 【线段树】jzoj1537 pot 纪中集训提高B组
2019-08-14 做题经验谈