【学习笔记】动态dp

概述

动态$dp$是一类需要对$dp$的输入数据进行修改，并在修改后要快速查询的问题。

求解动态$dp$最基本的思路是分治。

一直在想动态$dp$是不是叫动态动态规划（误

例题

SPOJ 1716

 

从题目开始说起吧，这样会比较好说。

 

 

0

可以比较直观地看出线段树的做法。

每个节点，维护一个区间和，前缀最大和，后缀最大和，和最大子段和。

然后就可以单点修改，区间查询。

#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstring>
#include<queue>
#include<cstdlib>
using namespace std;
#define N 500005
#define ll long long
#define INF 0x3f3f3f3f
struct node{
    int sum,ms/*maxsum*/,ml,mr/*maxl,maxr*/;
}tree[N*4];
int n,a[N];
inline int rd()
{
    int f=1,x=0;char c=getchar();
    while(c<'0'||'9'<c){if(c=='-')f=-1;c=getchar();}
    while('0'<=c&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return f*x;
}
void PushUp(int i)
{
    tree[i].sum=tree[i<<1].sum+tree[i<<1|1].sum;
    tree[i].ml=max(tree[i<<1].sum+tree[i<<1|1].ml,tree[i<<1].ml);
    tree[i].mr=max(tree[i<<1|1].sum+tree[i<<1].mr,tree[i<<1|1].mr);
    tree[i].ms=max(max(tree[i<<1].ms,tree[i<<1|1].ms),tree[i<<1].mr+tree[i<<1|1].ml);
}
void build(int i,int l,int r)
{
    if(l==r)
    {
        tree[i].sum=tree[i].ml=tree[i].mr=tree[i].ms=a[l];
        return ;
    }
    int mid=(l+r)>>1;
    build(i<<1,l,mid);
    build(i<<1|1,mid+1,r);
    PushUp(i);
}
void update(int i,int pos,int val,int l,int r)
{
    if(l==r)
    {
        tree[i].ms=tree[i].ml=tree[i].mr=tree[i].sum=val;
        return ;
    }
    int mid=(l+r)>>1;
    if(pos<=mid)
        update(i<<1,pos,val,l,mid);
    else update(i<<1|1,pos,val,mid+1,r);
    PushUp(i);
}
node query(int i,int li,int ri,int l,int r)
{
    if(l<=li&&ri<=r)
        return tree[i];
    int mid=(li+ri)>>1;
    if(r<=mid) return query(i<<1,li,mid,l,r);
    else if(l>mid) return query(i<<1|1,mid+1,ri,l,r);
    else
    {
        node x=query(i<<1,li,mid,l,r),y=query(i<<1|1,mid+1,ri,l,r),res;
        res.sum=x.sum+y.sum;
        res.ml=max(x.sum+y.ml,x.ml);
        res.mr=max(y.sum+x.mr,y.mr);
        res.ms=max(max(x.ms,y.ms),x.mr+y.ml);
        return res;
    }
}
int main()
{
    n=rd(); 
    for(int i=1;i<=n;i++)
        a[i]=rd();
    build(1,1,n);
    int Q=rd();
    while(Q--)
    {
        int opt=rd();
        if(opt==1)
        {
            int x=rd(),y=rd(),tmp;
            if(x>y) tmp=x,x=y,y=tmp;
            printf("%d\n",query(1,1,n,x,y).ms);
        }
        else if(opt==0)
        {
            int x=rd(),y=rd();
            update(1,x,y,1,n); 
        }
    }
    return 0;
}

 

1

那么动态$dp$是怎么做的呢

先不考虑修改，我们来想想一个正常的$dp$怎么来求全局最大子段和。

定义状态$f[i]$表示以$i$结尾的最大子段和，$g[i]$表示$1~i$的最大子段和

转移如下：
$f[i]=max(f[i-1]+a[i],a[i])$

$g[i]=max(g[i-1],f[i-1]+a[i],a[i])$

重定义矩阵乘法：把$*$重定义为$+$，$+$重定义为取$max$

即：

 

 把式子写成矩阵的形式（设转移矩阵为$C$

 

 

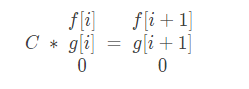
可以算出转移矩阵：

 

 

 

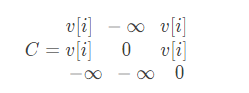
然后求$[l,r]$的值就是一个区间矩阵乘法，可以用线段树维护（还是要用线段树

#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#include<iostream>
#include<cstdio>
using namespace std;
#define N 500005
#define INF 0x3f3f3f3f
#define LL long long
int rd()
{
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1; c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48); c=getchar();}
    return f*x;
}
int n,a[N];
struct Matrix{
    int m[4][4];
    Matrix(){ memset(m,0,sizeof(m)); }
    int* operator [](int i){ return m[i]; }
};
Matrix operator * (Matrix a,Matrix b)
{
    Matrix c;
    for(int i=1;i<=3;i++)
        for(int j=1;j<=3;j++)
            c[i][j]=-INF;
    for(int i=1;i<=3;i++)
        for(int k=1;k<=3;k++)
            for(int j=1;j<=3;j++)
                c[i][j]=max(c[i][j],a[i][k]+b[k][j]);
    return c;
}
Matrix tree[N<<2];
void PushUp(int i)
{
    tree[i]=tree[i<<1]*tree[i<<1|1];
}
void Build(int i,int l,int r)
{
    if(l==r)
    {
        tree[i][1][1]=tree[i][1][3]=tree[i][2][1]=tree[i][2][3]=a[l];
        tree[i][1][2]=tree[i][3][1]=tree[i][3][2]=-INF;
        tree[i][2][2]=tree[i][3][3]=0;
        return ;
    }
    int mid=(l+r)>>1;
    Build(i<<1,l,mid);
    Build(i<<1|1,mid+1,r);
    PushUp(i);
}
void Modify(int i,int l,int r,int pos,int val)
{
    if(l==r)
    {
        tree[i][1][1]=tree[i][1][3]=tree[i][2][1]=tree[i][2][3]=val;
        return ;
    }
    int mid=(l+r)>>1;
    if(pos<=mid) Modify(i<<1,l,mid,pos,val);
    else Modify(i<<1|1,mid+1,r,pos,val);
    PushUp(i);
}
Matrix Query(int i,int l,int r,int ql,int qr)
{
    if(ql<=l&&r<=qr) return tree[i];
    int mid=(l+r)>>1;
    if(qr<=mid) return Query(i<<1,l,mid,ql,qr);
    else if(ql>mid) return Query(i<<1|1,mid+1,r,ql,qr);
    return Query(i<<1,l,mid,ql,qr)*Query(i<<1|1,mid+1,r,ql,qr);
}
int main()
{
    n=rd();
    for(int i=1;i<=n;i++)
        a[i]=rd();
    Build(1,1,n);
    int Q=rd();
    while(Q--)
    {
        int opt=rd(),x=rd(),y=rd();
        if(opt==0)
        {
            a[x]=y;
            Modify(1,1,n,x,y);
        }
        else
        {
            Matrix ans=Query(1,1,n,x,y);
            printf("%d\n",max(ans[2][1],ans[2][3]));//
        }
    }
    return 0;
}