HDU2196 Computer【换根dp】

题目传送门

题意：

给定一个 $N$ 个点的树，第 $i$ 条边的长度是 $A_i$ ，求每个点到其他所有点的最长距离。
数据范围：
$n ≤ 10000$ ， $A_i ≤ 10_9$

分析

首先，从随便哪个节点（ $1$ 号节点（工具人））开始进行 $dfs$ ，处理出所有点到 $1$ 的距离 $dis[i]$

然后，考虑 $i$ 号节点的最远点。

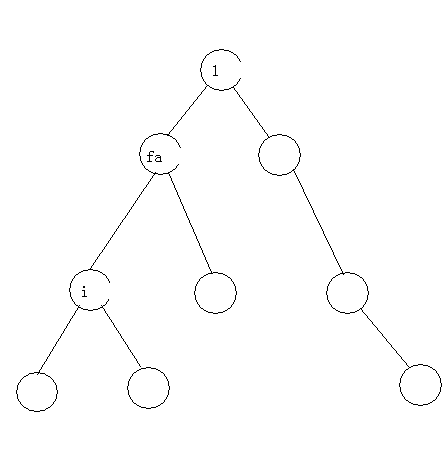
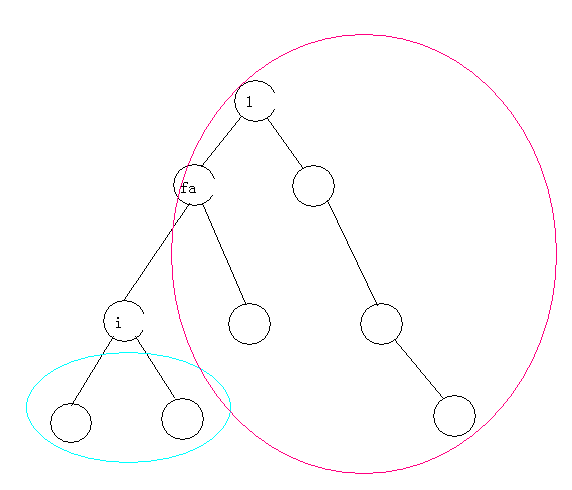
有两种情况：

一种是最远点在 $i$ 的子树内，直接求就完事了（之前我们在以 $1$ 为根的时候已经干过这件事情了）

另外一种就是经过了 $i$ 和他父亲的那一条边，最远点在父亲的其它儿子中（或者是父亲的父亲的儿子中，当然，在把父亲看成根的情况下，就是父亲的其它儿子中，并且根据换根的做法，之前根已经被换到了父亲，答案是现成的）

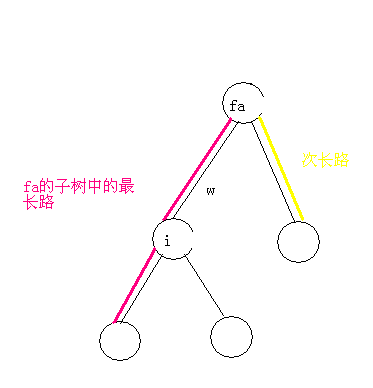
设离 $i$ 最远的距离为 $dist$ ，它父亲的子树中（以 $1$ 为根节点形成的数）离它父亲最远的距离为 $d1$ ，不在它父亲的子树中（通过了父亲<->爷爷这条边的）离它父亲最远的距离为 $d2$ ， $i$ 和它父亲的的那一条边的权值为 $w$

这种情况下， $dis=max(d1,d2)+w$

对于点 $i$ 的答案，两种情况取 $min$ 就可以啦。

但是这样还存在一个问题，就是如果父亲的子树中离父亲最远的那条路经过了 $i$ ，那么 $dis$ 就不能从 $d1$ 推过来，因为如果 $max(d1,d2)=d1$ ，那就是 $dis=d1+w$ ，而这肯定是不成立的， $d1$ 就包含了 $w$ 和 $i$ 到 $i$ 子树中最远的路。

那么还需要维护一个次长路，当 $i$ 在父亲到父亲子树中最远点的路径上时，要用次长路更新（这种情况下，这个次长路就是父亲的除 $i$ 之外的最大儿子。

 1 #include<cstdio>
 2 #include<algorithm>
 3 #include<cstring>
 4 #include<vector>
 5 #include<queue>
 6 using namespace std;
 7 #define N 10005
 8 #define INF 0x3f3f3f3f
 9 #define ll long long
10 int rd()
11 {
12     int f=1,x=0;char c=getchar();
13     while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
14     while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
15     return f*x;
16 }
17 int n;
18 int d1[N]/*距离i最长长度*/,d2[N]/*距离i次长长度*/;
19 //d1[] d2[]都是子树i以内的 
20 int son[N]/*最长长度对应儿子编号*/;
21 int anc[N]/*父亲方向最长长度(子树以外最长长度)*/;
22 int ans[N];//答案
23 struct node{
24     int v,w;
25 }; 
26 vector<node>G[N];
27 void dfs(int u,int f)
28 {
29     for(int i=0;i<G[u].size();i++)
30     {
31         int v=G[u][i].v,w=G[u][i].w;
32         if(v==f) continue;
33         dfs(v,u);
34         if(d1[u]<d1[v]+w)
35         {//从这个儿子能得到目前最长的长度 
36             d2[u]=d1[u];
37             son[u]=v;
38             d1[u]=d1[v]+w;
39         }/*要写else 大儿子和二儿子要不一样*/
40         else if(d2[u]<d1[v]+w)
41             d2[u]=d1[v]+w; 
42         /*
43         d2[v]不会被纳入答案中
44         大儿子和二儿子要不一样
45         无论如何都不会轮到d2[v]来做贡献
46         如果d1[v]可以贡献 就贡献了 d2[v]也不会被用到 
47         如果d1[v]不能贡献 d2[v]就更不会被用到了 
48         */
49     }
50     ans[u]=d1[u];
51 }
52 void dfs2(int u,int f)
53 {
54     for(int i=0;i<G[u].size();i++)
55     {
56         int v=G[u][i].v,w=G[u][i].w;
57         if(v==f) continue;
58         if(v!=son[u])
59             anc[v]=max(anc[u]+w,d1[u]+w);
60         else anc[v]=max(anc[u]+w,d2[u]+w);
61         ans[v]=max(ans[v],anc[v]);
62         dfs2(v,u);
63     }
64 }
65 int main()
66 {
67     while(scanf("%d",&n)!=EOF)
68     {
69         for(int i=2;i<=n;i++)
70         {
71             int v=rd(),w=rd();
72             node t;t.v=v,t.w=w;
73             G[i].push_back(t);
74             t.v=i;
75             G[v].push_back(t);
76             d1[i]=d2[i]=son[i]=anc[i]=ans[i]=0;
77         }
78         d1[1]=d2[1]=son[1]=anc[1]=ans[1]=0;
79         dfs(1,0);
80         dfs2(1,0);
81         for(int i=1;i<=n;i++)
82         {
83             printf("%d\n",ans[i]);
84             G[i].clear();
85         }    
86     }
87     return 0;
88 }