快速质因数分解及素性测试&ABC142D
首先，这个整数的标准分解非常的显然易见对吧：
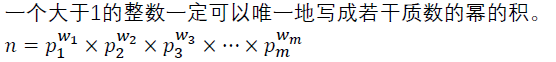
一般我们要把一个数分解成这个样子我们可以这样写：
1 #include<cstdio> 2 int p[105],w[105],k; 3 void factorize(int n) 4 { 5 for(int i=2;i*i<=n;i++) 6 if(n%i==0) 7 { 8 p[++k]=i; 9 while(n%i==0) 10 n/=i,w[k]++; 11 } 12 if(n!=1) 13 p[++k]=n,w[k]=1; 14 } 15 int main() 16 { 17 int n; 18 scanf("%d",&n); 19 factorize(n); 20 for(int i=1;i<k;i++) 21 printf("%d^%d*",p[i],w[i]); 22 printf("%d^%d",p[k],w[k]); 23 }
由于是分解质数，而且质数除了2之外都是奇数，所以可以在枚举i的时候每次i+=2
例题：ABC142D（手边没有什么好题了，只是因为最近做到了它2333）
要找互质的公因数，就相当于找最大公因数的最多互质的因数。（这个表述...相信你们能懂
之前写一直T了，于是找了另外一种方法，后面才发现之前的哪里有问题
1 #include<cstdio> 2 #include<algorithm> 3 #include<map> 4 using namespace std; 5 #define N 100005 6 #define ll long long 7 #define MOD 1000000007 8 ll x,y; 9 map<ll,bool> vis; 10 ll p[N]; 11 int pn; 12 ll gcd(ll a,ll b) 13 { 14 if(b==0) return a; 15 else return gcd(b,a%b); 16 } 17 int main() 18 { 19 scanf("%lld %lld",&x,&y); 20 ll d=gcd(x,y); 21 int ans=1; 22 if(d%2==0) ans++; 23 while(d%2==0) 24 d/=2; 25 for(ll i=3;i*i<=d;i+=2)//写成i<=d/i就可以不开ll 否则不开ll就会乘爆 然后T掉 26 if(d%i==0) 27 { 28 ans++; 29 while(d%i==0) 30 d/=i; 31 } 32 if(d!=1) ans++; 33 printf("%d\n",ans); 34 return 0; 35 }
就是我注释的那个地方，要注意那样的BUG了
最后采用了这种写法：
1 #include<cstdio> 2 #include<algorithm> 3 #include<map> 4 #include<vector> 5 #include<cmath> 6 using namespace std; 7 #define N 100005 8 #define ll long long 9 #define MOD 1000000007 10 ll x,y; 11 map<ll,bool> vis; 12 ll p[N]; 13 int pn; 14 vector<ll>st; 15 ll gcd(ll a,ll b) 16 { 17 if(b==0) return a; 18 else return gcd(b,a%b); 19 } 20 bool is_prime(ll x) 21 { 22 if(x==1) return 0; 23 if(x==2||x==3) return 1; 24 if(x%6!=1&&x%6!=5) return 0; 25 int s=sqrt(x); 26 for(int i=5;i<=s;i+=6) 27 if(x%i==0||x%(i+2)==0) 28 return 0; 29 return 1; 30 } 31 int solve(ll n) 32 { 33 int ans=1; 34 if(n==1) return 1; 35 ll i=0; 36 while(i<n) 37 { 38 if(is_prime(n)) 39 { 40 st.push_back(n); 41 if(vis[n]==0)ans++; 42 vis[n]=1; 43 return ans; 44 } 45 for(int i=2;i<n;i++) 46 { 47 if(n%i==0) 48 { 49 st.push_back(i); 50 if(vis[i]==0)ans++; 51 vis[i]=1; 52 n/=i; 53 break; 54 } 55 } 56 } 57 st.push_back(n); 58 if(vis[n]==0)ans++; 59 vis[n]=1; 60 return ans; 61 } 62 int main() 63 { 64 scanf("%lld %lld",&x,&y); 65 ll d=gcd(x,y); 66 printf("%d\n",solve(d)); 67 return 0; 68 }
其实感觉和上面的做法差不多，直接看也就能看懂，但是网上据说是$n^{1/4}$的复杂度，那么还是了解一下，也没有什么坏处。（对于这道题来说其实不需要存因数的啦）
关于is_prime的素数判断，还是说一下吧。
如果不加这个判断，那么在$n$变成一个很大的质数的时候，这个算法就会退化到$O(n)$级别。
对于每一个$>=5$的数可以表示为$6x-1$（也相当于$6x+5$）,$6x$,$6x+1$,$6x+2$,$6x+3$,$6x+4$,$6x+5$中的一种。
而$6x$,$6x+2=2(3x+1)$,$6x+3=3(x+1)$,$6x+4=2(3x+2)$，都不可能是素数。
所以我们对于一个数n，直接先判断它模$6$是否余$5$或余$1$，不是的话直接返回false
但是是的话也不一定是素数，还要再判断一下。
每个数都能进行质因数分解，所以我们只要判断用它除前面的素数能否除尽就可以了.
$6x+1$,$6x+5$这样的数显然不可能除的尽$2$和$3$，所以我们从$5$开始判断。
下一个除以$7$，按照上面的讨论，下一个为$11$和$13$。
网上有人说，以此类推，可以把步长增加到$6$来加快运行速度。
不知道怎么证明，但是验证了一下是对的。（怎么感觉好水...）
update2019.10.9 关于把步长增加到$6$
发现自己好傻啊
前面已经说了，3以后的质数都是除以6余1或者5的数
那么连续的两个质数差为2
当然，除以6余1或者5的数不一定都是质数，不过这没有关系，我们不一定要让除数是一个质数。
莫名其妙地就干完了这篇博客。
写得好水呀。
嘤嘤嘤我在干什么。
