唯一分解定理 约数和倍数 学习笔记

唯一分解定理

1、算数基本定理

对于任何一个大于 1 的整数 a，a 一定能分解为若干个质数的幂的乘积形式，且该分解是唯一的。即

$a=p_1^{r_1}p_2^{r_2}...p_s^{r_s}$

这是一个很重要的结论。数论的基础。

2、所有正约数的个数为$(1+r_1)(1+r_2)...(1+r_s)$

要记住证明：

对于一种质因子$p_i^{r_i}$，必然可以贡献一个因子$p_i^0,p_i^1,...,p_i^{r_i}$共$r_i+1$个数

从每一个质因子中取出一个数相乘即可得到原数的一个因子。

根据乘法原理即可得到

3、所有正整数的和为$(1+p_1+p_1^2+...+p_1^{r_1})...(1+p_s+...)$

也要记住证明：

对于一种质因子$p_1^{r_1}$，它可以提供的因数的因数有$(1,p_1,p_1^2,...,p_1^{r_1})$

若其他所有质因子可以提供的因数有$x_i$

那么可以得到所有因数为$x_i$，$p_1 x_i$，$p_1^2 x_i$...

那么所有数的和为$x_i+p_1 x_i+...=x_i*(1+p_1+p_1^2+...+p_1^{r_1})$

约数和倍数

1、若$b\in Z,a\in\{x\in Z|x≠0\}$若有$b=aq$，那么我们称b为a的倍数，a为b的因数，b能够被a整除，a能够整除b，$a|b$

由$0=a*0$可得，0是所有数的倍数，所有是0的因数，0能够被所有数整除，所有数都能整除b

2、

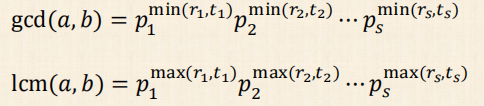
3、

对于条件1，假设$gcd(a,b)=x$，$a,b$还有公约数$y$，则$a=ka$，$b=kb$，$x=gcd(ka,kb)=kgcd(a,b)$，得证。