BZOJ 3384 上帝与集合的正确用法

上帝与集合的正确用法

【问题描述】

【输入格式】

第一行一个T，接下来T行，每行一个正整数p，代表你需要取模的值。

【输出格式】

T行，每行一个正整数，为答案对p取模后的值。

【样例输入】

3
2
3
6

【样例输出】

0
1
4

【数据范围】

对于100%的数据，T<=1000，p<=10^7
题解：
 

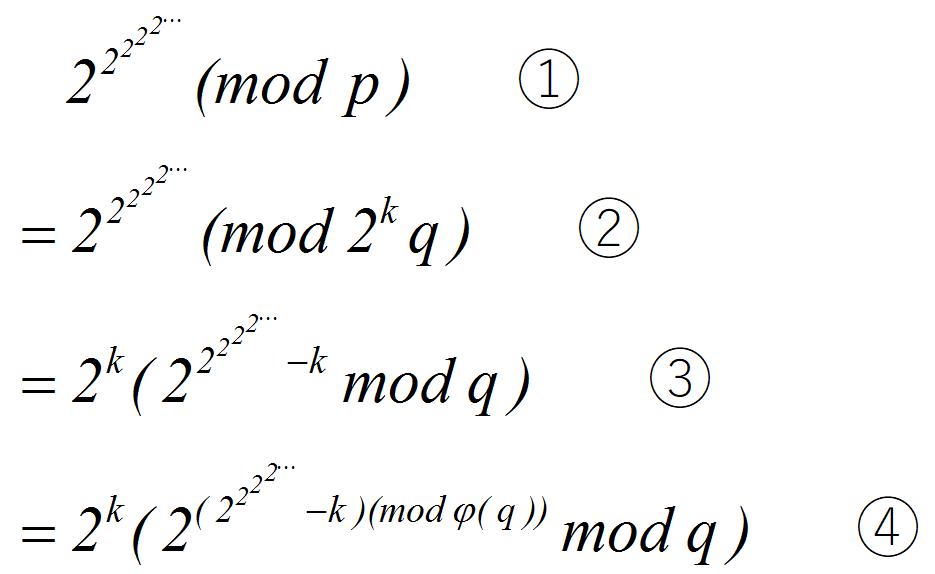
①->②：把模数 p 拆成 2kq 的形式，其中 q 是奇数

②->③：

将上式左右同除以2k

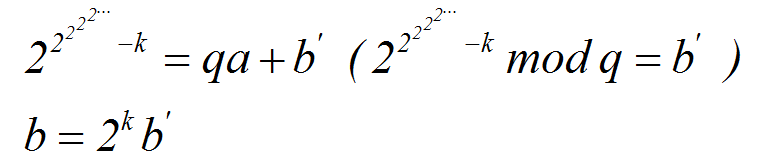
不会同余的蒟蒻只能这么推了

③->④:

此时 q 是奇数，必定与 2n 互质

则套用欧拉定理

考虑一个数的 phi 必定比它本身的值小

那么如此递归下去模数会变为 1，则返回 0

回溯得到答案

 1 #include<cmath>
 2 #include<cstdio>
 3 #include<cstdlib>
 4 #include<cstring>
 5 #include<iostream>
 6 #include<algorithm>
 7 using namespace std;
 8 int n;
 9 inline void Scan(int &x)
10 {
11     char c;
12     bool o = false;
13     while(!isdigit(c = getchar())) o = (c != '-') ? o : true;
14     x = c - '0';
15     while(isdigit(c = getchar())) x = x * 10 + c - '0';
16     if(o) x = -x;
17 }
18 int Phi(int x)
19 {
20     int ans = x;
21     for(int i = 2; i * i <= x; ++i)
22     {
23         if(!(x % i))
24         {
25             while(!(x % i)) x /= i;
26             ans /= i, ans *= (i - 1);
27         }
28     }
29     if(x ^ 1) ans /= x, ans *= (x - 1);
30     return ans;
31 }
32 int Pow(int x, int n, int mod)
33 {
34     int sum = 1;
35     while(n)
36     {
37         if(n & 1) sum = (long long) sum * x % mod;
38         x = (long long) x * x % mod;
39         n >>= 1;
40     }
41     return sum % mod;
42 }
43 int Work(int p)
44 {
45     if(p == 1) return 0; 
46     int k = 0;
47     while(!(p & 1)) p >>= 1, ++k;
48     int phi = Phi(p);
49     int s = (Work(phi) - k) % phi;
50     if(s < 0) s += phi;
51     return Pow(2, s, p) << k;
52 }
53 int main()
54 {
55     Scan(n);
56     int p;
57     for(int i = 1; i <= n; ++i)
58     {
59         Scan(p);
60         printf("%d\n", Work(p));
61     }
62 }
posted @ 2017-06-14 15:02  草根柴鸡  阅读(282)  评论(0)  编辑  收藏  举报